시계열 데이터 분석 관련 공부 - #1. Intro to Time Series Data

Reference

• 충북대학교 강의자료
• https://www.analyticsvidhya.com/blog/2015/12/complete-tutorial-time-series-modeling/
• https://blog.naver.com/chunjein/100173242445

시계열 데이터 분석(Time Series Data Analysis)

0. 시계열 데이터의 정의

시간의 흐름에 따라 관찰된 데이터(초, 분, 시간, 일, 주, 월, 분기, 년 등의 구간)

1. 시계열 분석 개요

• 시계열 자료의 관측 시점 간 거리는 동일하다고 가정한다
• 주어진 시계열 내에서 결측치가 존재할 경우, 유사 시점의 값으로 대체하거나 평균 등의 값으로 보정한다.
• 시간의 흐름에 따른 특성을 기준으로 모형을 설정하기에, 자료의 과거 정보를 기준으로 미래를 예측함

시계열 데이터의 자기상관성

시점 간의 상관관계를 말하며, 일정한 기간 동안 증가(또는 감소)가 지속된다면 양의 상관성을 갖는다. 반대로, 일정한 기간 내에서 증감이 반복될 경우에는 음의 상관성을 갖는다.

2. 분석 목적

• 시계열을 따라 변하는 값을 예측하기 위함
• 시계열 데이터 자체의 특성(경향성, 주기, 계절성, 불규칙성 등)을 파악하기 위함
  - 시계열 데이터 특성의 특성(ex. 불규칙성 자체의 원인)을 파악하기 위함

3. 유형

3.1. 단변량 시계열 분석 (단순 시계열 분석)

단 1개의 변수(Factor)만을 분석하는 시계열 분석 (ex. ARIMA 모델)

3.2. 다변량 시계열 분석 (다중 시계열 분석)

단일 변수 이외에, 해당 변수에 영향을 주는 원인 변수까지 포함하여 시계열 분석 (ex. 계량경제 모델, 전이함수 모델, 개입모델, 상태공간 모델, 다변량 ARIMA,etc)

4. 시계열 데이터 분해(Decomposition)

4.1. 분해 by 체계성 여부

• Systematic Components : 일관성 또는 재현(or 재발) 가능성이 있는 요인
• Non-systematic Components : 일반화하여 모델링할 수 없는 요인

4.2. 시계열 데이터 설명 요인 구조화

• 1) Level : 시계열 데이터의 평균값을 의미. (데이터의 전반적 수준치를 나타냄; The average value in the series)
• 2) Trend($T_{t}$) : 시계열 데이터 내에서 증가하는 경향 또는 감소하는 경향이 있는 값
• 3) Seasonality($S_{T}$) : 시계열 데이터 내에서 반복적으로 관측되는 단기적 사이클
• 4) Noise($\epsilon_{t}$) : 시계열 내에서의 랜덤한 변이값(variation) 내지 오차(error)

4.3. 가법과 승법 분해 (Additive Model & Multiplicative Mdel)

• Additive Model : $y(t)$ $=$ $Level + T_{t} + S_{t} + \epsilon_{t}$
• Multiplicative Model : $y(t)$ $=$ $Level * T_{t} * S_{t} * \epsilon_{t}$

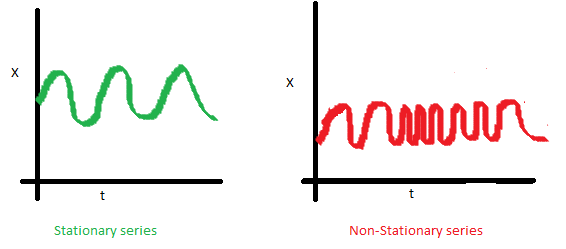
4.4. 정상성 (Stationarity)

시계열 데이터의 평균, 분산이 일정하며, 공분산이 오직 시차에만 의존할 경우 해당 시계열 데이터는 정상성이 있다고 정의한다.

4.4.1. 정상(stationary) 시계열의 요구

• 대부분의 시계열 데이터는 비정상성 시계열 자료 $\rightarrow$ 분석하기 쉬운 정상성 시계 열로 변환하는 과정을 거친다.
  $\because$ 안정 시계열이 되기 이전까지는 시계열 모델을 구축할 수가 없음

• 정상성 검정방법: Dickey Fuller Test of Stationarity

• 정상화 방법: detrending, differencing, Seasonality 등
  (1) Detrending(탈추세) : simply remove the trend component from the time series.
  (2) Differencing(차분): the Integration part in AR(I)MA
  (3) Seasonality(계절성): easily be incorporated in the ARIMA model directly

5. 정상 시계열의 3가지 특징

정상 시계열 $\rightarrow$ 평균, 분산, 공분산에 대한 정의를 모두 만족한다

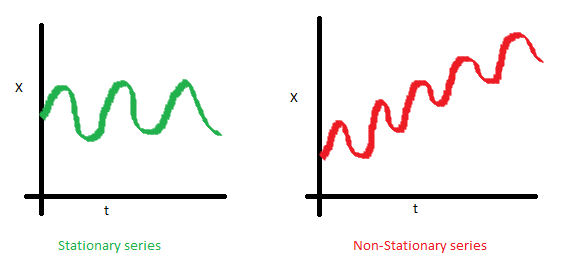
5.1. 평균 : 시간의 추이와 관계 없이 평균이 일정

$\rightarrow$ 평균이 일정하지 않은 시계열은 차분(difference)을 통해 정상화

차분 : 현시점 자료($x_{t}$)에서 이전 시점 자료($x_{t-1}$)를 빼는 것 ($x_{t}$-$x_{t-1}$)

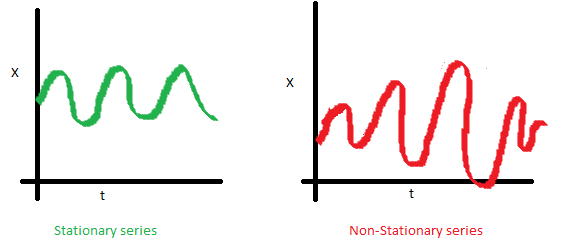
5.2. 분산 : 시간의 추이와 관계 없이 분산이 일정

$\rightarrow$ 분산이 일정하지 않은 시계열은 변환(transformation)을 통해 정상화

3) 공분산: 두 시점 간의 공분산이 기준시점과 무관

$\rightarrow$ 공분산도 시차($\triangle t$)에만 의존할 뿐, 특정 시점($t_{i}, i\in\real$)에는 의존하지 않음