1. 왜 2-view geometry 필요?
- 왜 3d point의 위치를 알기 위해 왜 2개 이상의 이미지가 필요한지
mapping 관점
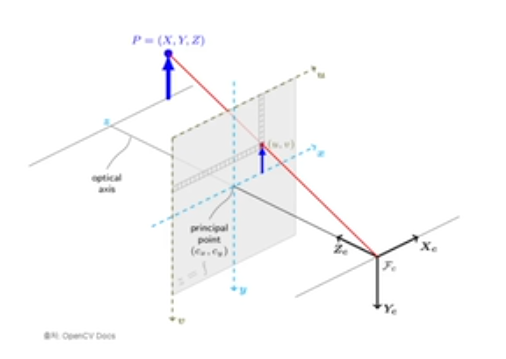
- 3D에서 2D로의 mapping은 할 수 있다
- 그럼 2D을 3D로 mapping하는 것은?
- intrinsic와 extrinsic을 알고 있다면 inverse해서 구할 수 있다.
- 하지만 실제 세상에서 extrinsic을 알지 못한다. extrinsic을 알고 있다는 것은 이미 3D point의 위치를 알고 있다는 것을 의미한다 -> depth를 구할 수 없다
- 단일 카메라에서 한장의 이미지로 3D를 2D로 mapping할 수 있지만, 2D를 3D로 mapping하기 위해서는 여러장의 이미지가 필요하다!
- 최소 2장의 view가 필요하다
- 번외로...
- RGB-D의 경우 depth가 주어진다 -> 3D point의 위치를 이미지 하나로도 알 수 있다
- 그럼 RGB-D 카메라를 사용하면 SLAM을 안써도 되는거 아닌가?
- 아니다.
- RGB-D 카메라의 depth는 요동치는 경우가 많다. 센서 노이즈가 큰편이다.
- 이를 보정하기 위해 여러장의 이미지를 사용하여 VSLAM을 수행 -> 정확한 mapping정보를 받을 수 있다.
- depth을 알게 되었으니 이미지 한장으로부터 3D 공간을 재구성 할 수 있다.
- VSLAM의 목적은 mapping도 있지만 localization, 3D 공간 확장시키는 목적도 있다.
- 따라서 RGB-D로 depth를 아는 것에서 끝나지 않고 여러장의 이미지가 필요하게 된다.
motion 관점
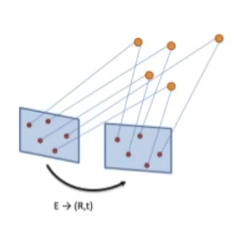
- 카메라가 얼마나 이동했는지 구해야한다 = 이미지 간의 카메라 프레임의 pose 이동(rigid body motion)을 구해야한다
- 모션 정보는 proprioceptive sensor를 통해 받으면 바로 알 수 있지만 VSLAM에서는 visual 정보만으로 해석해야한다.
- 따라서 영상 정보로부터 모션 정보를 추론할 수 있어야한다
- 모션 정보를 얻기 위해서는 두 개의 이미지 간의 기하학적 상관관계에 대해 알아야한다.
2. Epipolar geometry (2-view geometry)
Epipolar line
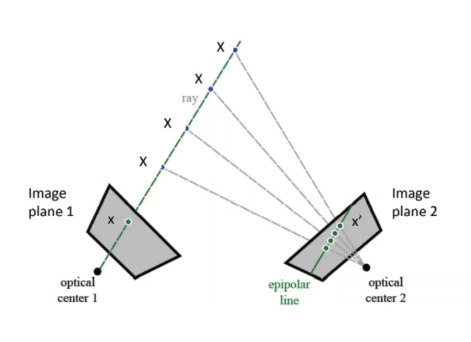
- 단안 카메라의 경우 : 왼쪽은 과거, 오른쪽은 현재 시점
- 스테레오 카메라의 경우 : 왼쪽, 오른쪽 카메라
- 2-view geometry는 단안, 스테레오 모든 경우에 적용가능하다
- 왼쪽 카메라
- 3D point를 2D 이미지로 투영하는 과정
- image plane에 x라는 상이 맺힌다
- optical center(카메라 center)에서 3D point까지 그린 직선 = 초록색 선 = ray
- ray : 빛이 이동한 경로 / VSLAM에서는 3D point가 2D로 project될때의 직선
- 오른쪽 카메라
- ray를 본다
- ray가 투영된다 -> 재투영(reprojection)
- 왜 재투영? 원래 2D에 있던 점을 3D의 형태로 바꾼 후에 다시 다른 시점에서 2D로 투영했기 때문
- ray를 투영한 직선 = epipolar line
- epipolar line이 중요한 이유
- 동시에 바라보는 3D point는 무조건 epipolar line에 있기 때문
- 오른쪽 카메라 이미지 속 어떤 픽셀에 포인트가 맺힐지 epipolar line으로 추론할 수 있게 된다 -> line이 없는 곳에는 절대 상이 맺힐 수 없다
- 카메라의 rigid body motion을 구하기 위해서는 optical center 1과 2의 rotation과 translation의 차이를 구해야한다. 이를 위해서는 x1과 x'의 correspodence가 정확하게 맞아야하고 이는 epipolar line에 3D point가 있을 수 밖에 없다라는 전제 조건이 유용
Epipole
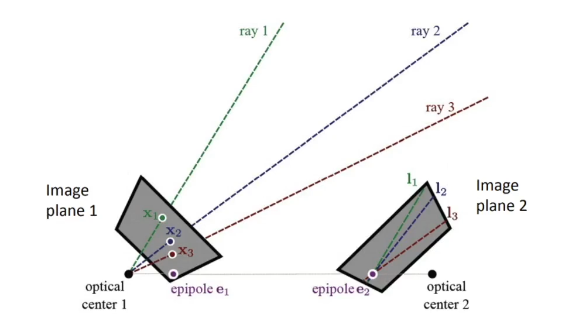
- 왼쪽 카메라가 3개의 point를 보고 있다
- 각각의 상들마다 ray를 만든다
- ray들을 오른쪽 카메라에 재투영 -> epipolar line 3개가 생긴다
- 종종 3개의 epipolar line이 한 점에서 교차(intersect)될 때가 있다. -> 이 점을 epipole이라고 부른다
- epipole의 기하학적 의미
- 모든 epipolar line은 공통적으로 교차하는 곳이 있다 = ray가 시작되는 점인 카메라 optical center
- epipole은 ray들이 intersect하는 곳과 동일
- 즉, 반대편 카메라의 optical center가 투영된다고 하면 그것이 epipole
- epipole이 보이는 경우는 지난 시점의 카메라의 위치가 현시점에서 보이는 경우
- 또한 반대 시점에서도 현재 시점의 optical center가 보여서 epipole이 맺힐 확률이 있다
특이한 Epipole 위치 (2가지)
1. 좌우가 같은 방향으로 바라볼 때 (좌우로 translation만 있는 경우)
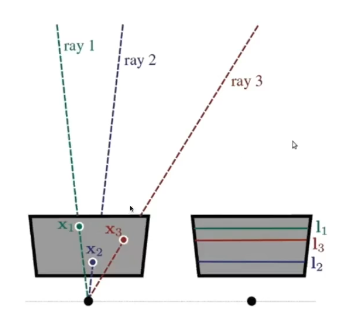
- 전방 스테레오 카메라를 사용할 때 자주 나타난다
- 이미지에 epipole이 없다
- 추가로 epipole이 이미지 밖에서도 맺히지 않는다 <- epipolar line이 평행하게 나타나기 때문이다
- 스테레오 카메라의 경우 calibration을 거치고 나서 rectification 과정을 수행한다 -> 이 과정에서 카메라들의 위치를 조금씩 이동시키면서 이미지를 warping을 해줘서 위와 같은 상황을 일부러 만들게 된다
- 왜 일부러 만드는가?
- 모든 epipolar line이 가로로 나타난다
- 왼쪽의 x1, x2, x3를 찾고 싶으면 correspondence를 찾을 때 각각 l1, l2, l3의 row를 찾으면 된다
- row에서 해당 픽셀을 찾는 것은 매우 쉽다(대각선으로 epipolar line이 있는 경우는 오래걸린다)
2. 하나의 이미지가 회전 없이 직진만 한 경우

- monocular VSLAM을 하는 로봇, 자동차에서 주로 나타난다
- epipole1과 epipole2가 직선에 놓이게 된다
- 서로 epipole이 보이지는 않지만 epipolar line이 방사 패턴으로 나타나게 된다
- ray는 line으로서의 방향성만 가지고 있기 때문에 어디서 시작되고 끝나는지 표현할 수 없다 -> 투영한 ray가 앞에서 투영된건지, 뒤에서 투영된건지 알 수 없다
- correspondence를 빨리 찾게 해준다는 이점은 없다
- 두 epipole을 보면 굳이 correspondence를 구하지 않아도 relative motion을 구할 수 있다 -> 회전값이 (0,0,0)인걸 바로 알 수 있고 추가적인 motion sensor가 있다면 거기서 바로 translation 값을 바로 씀으로써 얼마나 이동했는지 알 수 있다
Epipolar plane
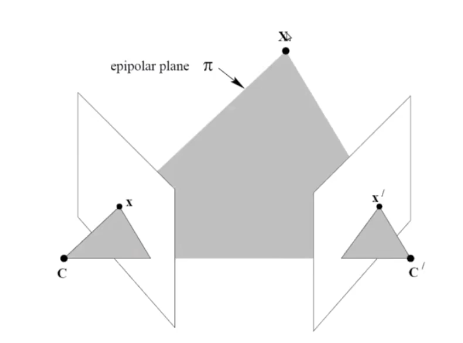
- 좌우 optical center와 3D point를 연결 (왼쪽 ray, 오른쪽 ray, 좌우 optical center를 연결)
- 이렇게 만들어진 삼각형을 epipolar plane (π)이라고 한다
- epipolar plane은 epipolar line, epipole에 대한 정보도 함께 포함하고 있다
- epipolar plane을 통해 epipolar geometry가 완성된다
baseline
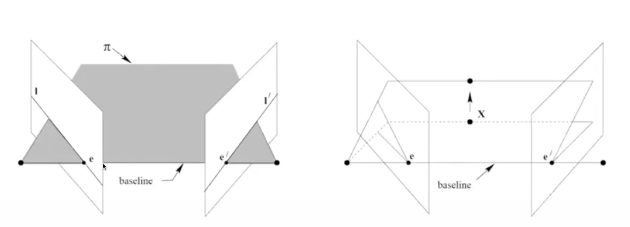
- 좌우 optical center을 연결했을 때 생기는 line
- 두 카메라 간의 거리값을 의미
- 스테레오 카메라에서 baseline의 크기가 클수록 삼각측량의 정확도가 높아진다는 말도 있다
- baseline의 특징
- baseline이 image plane을 통과하게 된다면 그 점이 epipole이 된다 = epipole은 baseline 위에 있다
- 모든 epipolar plane은 baseline을 포함하고 있다
- baseline과 ray들이 교차한다
- 하나의 이미지에서 여러 point를 측량하는 것이 가능하다 = 다양한 3D point의 위치가 있다 -> 그럼 각각의 epipolar plane을 만드는데 모든 plane들은 baseline을 기준으로 회전한다
- epipolar plane들의 모든 가능성을 epipolar pencil이라고 한다
correspondence가 생기는 3가지 조건
- 3D point x는 epipolar plane 위에 있어야한다.
- 모든 epipolar line들은 epipole과 교차해야한다
- 모든 baseline들은 epipole과 교차해야하며 모든 epipolar plane은 baseline을 포함하고 있어야한다
- 이러한 조건들을 기하학적으로 geometry constraint라고 한다(epipolar constraint)
- epipole, 2D image point, 3D point는 모두 동일한 plane 위에 있기 때문에 이를 coplanar constraint라고 하기도 한다. (coplanar = 동평면상의)
3. Essential Matrix / Fundamental Matrix
- epipolar geometry가 사용된다
Essential matrix란? (E matrix)
- epipolar constraint에 대한 정보를 담고 있는 matrix
- 즉, 두 카메라간의 회전과 이동에 관한 정보를 담고 있다
- calibration된 카메라들 사이의 관계를 의미한다 (정규화된 이미지 평면에서 대칭쌍들 사이의 기하학적인 관계)
- 3x3 형태의 matrix
- 카메라 간의 motion을 알기 위해서는 correspondence를 아는 것이 중요하다
- correspondence를 정확하게 얻어낼 수 있도록 해주는 것이 epipolar constraint이기 때문에 카메라 간의 motion을 알기 위해서는 Essential matrix를 알아내는 것이 중요!
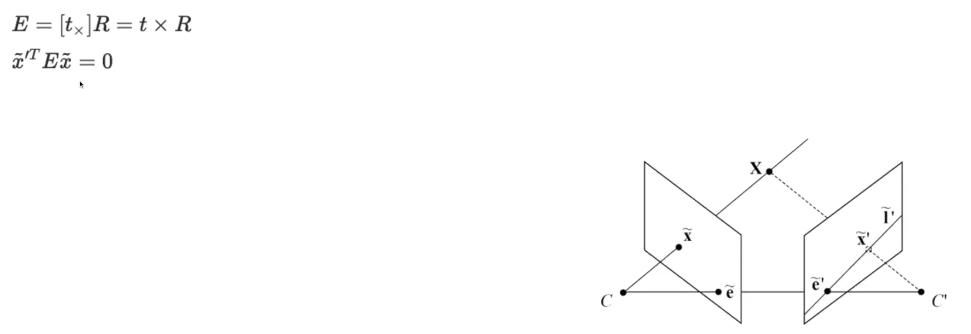
- essentail matrix는 두개의 2D point 즉, correspondence들을 이어주는 역할
- 왼쪽의 x와 오른쪽의 x'을 이어주면서 geometry constraint를 만들어준다
- E는 t(translation)와 R(rotation)의 cross prodect(외적)로 이루어져있다.
- t : 3x1 vector (x, y, z) , 외적을 하기 위해 3x3 matrix로 변경
- R : SO(3) rotation, 3x3
- 결과 E : 3x3
- essentail matrix를 구하고 나서 rotation와 translation으로 분해할 수 있다
- 하지만 이 수식을 그대로 사용하게 되면 문제가 있다
- x가 어떻게 표현되는지 모른다는 점이다!
- Essential Matrix를 구할 때 normalized image plane을 사용해서 x의 값이 소수점으로 나타난다
- 하지만 실제 이미지를 다룰 때는 픽셀로 위치를 표현한다
- 그래서 normalized image plane에서 픽셀 location으로 바꿔주는 정보가 필요하다
- 이게 K(intrinsic matrix)이다
Fundamental Matrix (F matrix)
- Essential Matrix with intrinsic matrix(K)
- 카메라 파라미터 정보까지 포함한 두 이미지의 실제 픽셀 좌표 사이의 기하학적 관계
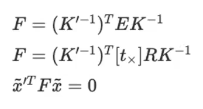
- 하나의 카메라인 경우 K matrix가 동일 / 스테레오의 경우 K matrix가 다르다
- 왼쪽 이미지의 픽셀정보와 오른쪽 이미지 픽셀 정보의 mapping 정보
Line search
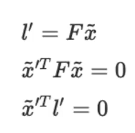
- 1번째 식 : x와 l'의 관계
- 3번째 식 : line과 point가 교차하게 된다면 두 개의 외적은 0이다
- x'가 왼쪽의 이미지에서 어떤 점과 correspondence를 이루는지 문제를 풀기 위해 모든 픽셀을 볼 필요없이 F matrix를 곱해서 나온 line만 보면 된다. 그리고 그 line과 외적을 하여 0이 나오는 픽셀들만 사용하면 된다
E/F Matrix algorithm
- essiential matrix를 구할 때는 5-point algorithm
- fundamental matrix를 구할 때는 8-point algorithm
8-point algorithm
- 최소 8개의 point correspondence가 존재할 때
- fundamental matrix
- essiential matrix
- 5자유도 : tx, ty, tz, rx, ry, rz -> scale이 제외되어 5개
- 데이터의 DoF를 아는 것은 중요하다
- 데이터를 추론하기 위해 필요한 최소한의 데이터의 수는 몇개인가?
- 데이터가 요구하는 DoF만큼의 데이터가 필요하다
- 최소한의 수로 문제를 해결하는 알고리즘 -> minimum solver
- 5-point algorithm은 5DoF를 가진 데이터를 추론하기 위해 5개의 데이터를 사용 -> minimum solver
- 8-point algorithm은 7DoF를 추론하기 위해 8개의 데이터 사용 -> non minimum solver
- 그럼 Fundamental Matrix를 계산하는 minimum solver는 7개의 데이터를 사용해야하는가? -> 원래 이게 맞다. 하지만 7개를 사용하는 경우 내부 구조가 매우 복잡하고 안되는 경우가 있어서 8-point algorithm를 사용한다.

- minimum DoF를 충족할 수 있을만큼의 x,y 데이터 쌍을 가지고 있다면 homogeneous system을 만들 수 있다 (A가 데이터의 쌍으로 만든것)
사용법 opencv
findFundamentalMat()recoverPose(): essential matrix- correspondence : feature descriptor간의 matching 정보
