MCMC and its diagnostics

텍스트### 1. Markov chain monte carlo(MCMC)

• Construct a markov chain whose stationary distribution = $\pi$ to draw samples from target distribution $\pi$.
• Running a markov chain leads to sampling from target distribution
• Ergoic markov chain has unique stationary distribution
• Bayesian inference can be done on markov chain samples, even when the posterior distribution is intractable.
• Definition of markov chain: $P(X^{(t+1)}|X^{(0)}, ..., X^{(t)})=P(X^{(t+1)}|X^{(t)})$
• Transition probability: $P_{ij}^{(t)} = p(X^{(t+1)}=j|X^{(t)}=i)$, time homogeneous condition: $P_{ij}$ is constant
• $\pi$ is a stationary distribution if $\pi_{j} = \sum_{i\in X}\pi_iP_{ij}, i.e. \pi^TP=\pi^T$
  

2. Metropolis-Hastings algorithm

• Metropolis-Hastings algorithm can be utilized even if we only know the kernel of the target distribution.
• Acceptance criterion is designed to meet the detailed balance condition
• Symmetric proposal density, extremely we can utilize uniform distribution of Bernoulli(0.5) for some special variables. Usually normal proposal density is utilized(random walk metropolis samples with a symmetric normal proposal).
• Practical issues
  • Burn-in(discard first several samples to remove the effect caused by the arbitrary starting point)
  • Thinning(only select Mth sample to obtain independent samples)

3. Gibbs Sampler

• Gibbs Sampler can be utilized when we know the full conditional distribution of target distribution.
• Fixed-scan draw is similar to gibbs sampler, while Metropolis-Hastings style acceptance criterion is added for each sequential parameter draw process.
  

4. Diagnostic methods and Practical issues

• Burn-in, Thinning
• Metropolis-hastings algorithm: random walk sampler, step size also should be tuned
  • Step size can be tuned separately for multivariate cases, but step size also can be tuned adaptively
  • $q(\cdot|\theta_n) = \mathcal{N}(\theta_n, \Sigma_n)$ where $\Sigma_n$ is a sample covariance matrix using posterior samples up to nth iteration
  • Adaptive updates should be stopped in some N<$\infty$ iteration
• To remove intial value effect, you can utilize burn-in or try MLE estimate as an intial value, or try different initial values and run chains separately

[Diagnostic Methods]

• TS plot
• Density plot
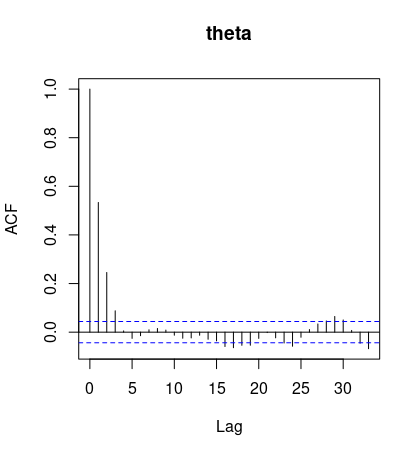
• Autocrrelation function(ACF plot)
• Effective sample size
• Gelman-rubin statistic(ANOVA test-like statistic)
• Remark: If autocorrelation remains high, we should consider thinning to increase effective sample size... Figure below is fine.