1. 미분과 수치 미분

미분 계수의 정의는 다음과 같다.

$f'({x}) = \displaystyle\lim_{h\to 0}{f({x+h}) - f({x})\over h}$

이를 프로그램으로 구현한다면 $\displaystyle\lim_{h\to 0}$ 부분이 문제가 생긴다.
수치적(numerical)으로 구현하면 일부 문제가 해결된다.

2. 수치 미분 구현

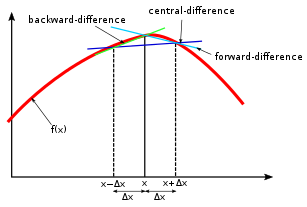
수치 미분에는 forward difference와 central difference가 있다.

forward difference는 구하려는 포인트부터 $\epsilon$ 만큼 앞에 있는 지점과 기울기로 미분계수를 구한다.

$f'({x}) \simeq \displaystyle {f({x+\epsilon}) - f({x})\over \epsilon}$

central difference는 구하려는 포인트부터 앞뒤로 $\epsilon$ 만큼 앞에 있는 지점 사이 기울기로 미분계수를 구한다.

$f'({x}) \simeq \displaystyle {f({x+\epsilon}) - f({x-\epsilon})\over 2\epsilon}$

정확도는 central difference가 높다.

그래프로 살펴보면 그 차이가 확실히 보인다.

정확한 증명은 테일러 급수로 이루어진다.

정확한 증명

테일러 급수

$f(a+u)\;=\;f(a)+u\frac{\mathrm{d} f}{\mathrm{d} x}+\frac{1}{2!}u^{2}\frac{\mathrm{d}^2 f}{\mathrm{d} x^{2}}+\frac{1}{3!}u^{3}\frac{\mathrm{d}^3 f}{\mathrm{d} x^{3}}+...$

forward difference의 경우,

$f(a+u)\;=\;f(a)+u\frac{\mathrm{d} f}{\mathrm{d} x}+\frac{1}{2!}u^{2}\frac{\mathrm{d}^2 f}{\mathrm{d} x^{2}}+\frac{1}{3!}u^{3}\frac{\mathrm{d}^3 f}{\mathrm{d} x^{3}}+...$

$f(a+u)-f(a)\;=\;u\frac{\mathrm{d} f}{\mathrm{d} x}+\frac{1}{2!}u^{2}\frac{\mathrm{d}^2 f}{\mathrm{d} x^{2}}+\frac{1}{3!}u^{3}\frac{\mathrm{d}^3 f}{\mathrm{d} x^{3}}+...$

${f(a+u)-f(a) \over u}\;=\;\frac{\mathrm{d} f}{\mathrm{d} x}+\frac{1}{2!}u\frac{\mathrm{d}^2 f}{\mathrm{d} x^{2}}+\frac{1}{3!}u^{2}\frac{\mathrm{d}^3 f}{\mathrm{d} x^{3}}+...$

${f(a+u)-f(a) \over u}-\frac{\mathrm{d} f}{\mathrm{d} x}\;=\;err(u)$

$err(u)\;=\;\frac{1}{2!}u\frac{\mathrm{d}^2 f}{\mathrm{d} x^{2}}+\frac{1}{3!}u^{2}\frac{\mathrm{d}^3 f}{\mathrm{d} x^{3}}+...$

로 $err(u)$가 $u$의 1차가 dominant하다.


반면, central difference의 경우,

$f(a+u)\;=\;f(a)+u\frac{\mathrm{d} f}{\mathrm{d} x}+\frac{1}{2!}u^{2}\frac{\mathrm{d}^2 f}{\mathrm{d} x^{2}}+\frac{1}{3!}u^{3}\frac{\mathrm{d}^3 f}{\mathrm{d} x^{3}}+...$

$f(a-u)\;=\;f(a)-u\frac{\mathrm{d} f}{\mathrm{d} x}+\frac{1}{2!}u^{2}\frac{\mathrm{d}^2 f}{\mathrm{d} x^{2}}-\frac{1}{3!}u^{3}\frac{\mathrm{d}^3 f}{\mathrm{d} x^{3}}+...$

$f(a+u)-f(a-u)\;=\;2u\frac{\mathrm{d} f}{\mathrm{d} x}+\frac{2}{3!}u^{3}\frac{\mathrm{d}^3 f}{\mathrm{d} x^{3}}+...$

${f(a+u)-f(a-u) \over 2u}\;=\;\frac{\mathrm{d} f}{\mathrm{d} x}+\frac{1}{3!}u^{2}\frac{\mathrm{d}^3 f}{\mathrm{d} x^{3}}+...$

${f(a+u)-f(a-u) \over 2u}-\frac{\mathrm{d} f}{\mathrm{d} x}\;=\;err(u)$

$err(u)\;=\;\frac{1}{3!}u^{2}\frac{\mathrm{d}^3 f}{\mathrm{d} x^{3}}+...$

로 $err(u)$가 $u$의 2차가 dominant하다.

코드로 구현하면 다음과 같다.

# central difference 사용
def numerical_diff(f, x, eps=1e-4):
    x0 = Variable(x.data - eps)
    x1 = Variable(x.data + eps)
    y0 = f(x0)
    y1 = f(x1)
    return (y1.data - y0.data)/(2*eps)

f = Square()
x = Variable(np.array(2.0))
dy = numerical_diff(f, x)
print(dy)

4.00000000000

3. 합성 함수의 미분

${y}=(e^{x^2})^2$를 수치 미분하면 다음과 같다.

def f(x):
    A = Square()
    B = Exp()
    C = Square()
    return C(B(A(x)))

x = Variable(np.array(0.5))
dy = numerical_diff(f, x)
print(dy)

3.2974426293330694

4. 수치 미분의 문제점

수치 미분은 함수와 $x$에 따라 오차가 커질 가능성이 있다.
비교적 작은 central difference라도

$err(u)\;=\;\frac{1}{3!}u^{2}\frac{\mathrm{d}^3 f}{\mathrm{d} x^{3}}+...$

오차가 $x$의 3차 미분이 dominant하므로 함수의 성향과 $x$에 따라 오차가 커진다.

또한 매개변수가 늘어남에 따라 계산량이 많아진다.

backpropagation과 비교한 표를 chatGPT로 생성해달라고 했다.

알고리즘	장점	단점
역전파(Backpropagation)	많은 파라미터를 가진 심층 신경망의 학습에 효율적입니다. 비선형성과 복잡한 활성화 함수를 처리할 수 있습니다. 최적화를 위한 정확한 기울기를 제공합니다.	심층 신경망에서 사라지는 기울기 문제와 폭주하는 기울기 문제가 있을 수 있습니다. 최적화 도중 국소 최소값에 머무를 수 있습니다. 세밀한 하이퍼파라미터 튜닝이 필요합니다.
수치 미분(Numerical Differentiation)	구현과 이해가 쉽습니다. 미분이 불가능한 함수를 포함한 모든 함수와 함께 사용할 수 있습니다. 다른 방법으로 계산된 기울기의 수치적 검사로 사용할 수 있습니다.	파라미터가 많을 경우 계산 비용이 높아집니다. 부동 소수점 연산과 수치적 불안정성으로 인한 수치 오류에 취약합니다. 복잡한 비선형성과 활성화 함수에서는 잘 작동하지 않을 수 있습니다.

---

Github: https://github.com/gsgh3016/Deep-Learning-from-Scratch3/blob/main/gamchan/part_1/step04.py