썸네일 사진은 프로젝트 발표를 위해 PPT에 삽입했던 컨셉화면입니다.
📢데이터분석 프로젝트
파이썬을 활용하여 데이터분석 및 데이터 시각화 프로젝트를 진행해보자
데이터분석 프로젝트 - 인플레이션 발표편
데이터분석 프로젝트 - 미세먼지 발표편
데이터분석 프로젝트 - 인플레이션 분석편
데이터분석 프로젝트 - 미세먼지 분석편
데이터분석 프로젝트 - 주제선정
데이터분석 및 시각화 프로젝트 2편
미세먼지 데이터로는 만족을 하지 못하는 열정적인 나이기에
이번에는 내가 관심이 많고, 흥미를 가지고 있는 경제에 관해 분석해보기로 했다.
남들 하나 할때 두개의 주제를 수행하는 것에 대해 큰 부담이 되었지만 남들보다 많은 시간을 투자하면 되기 때문에 상관이 없다.
인플레이션에 대항하는 법 : 투자 라는 주제로 데이터분석 및 시각화를 진행해보자
📢경제 데이터 준비하기
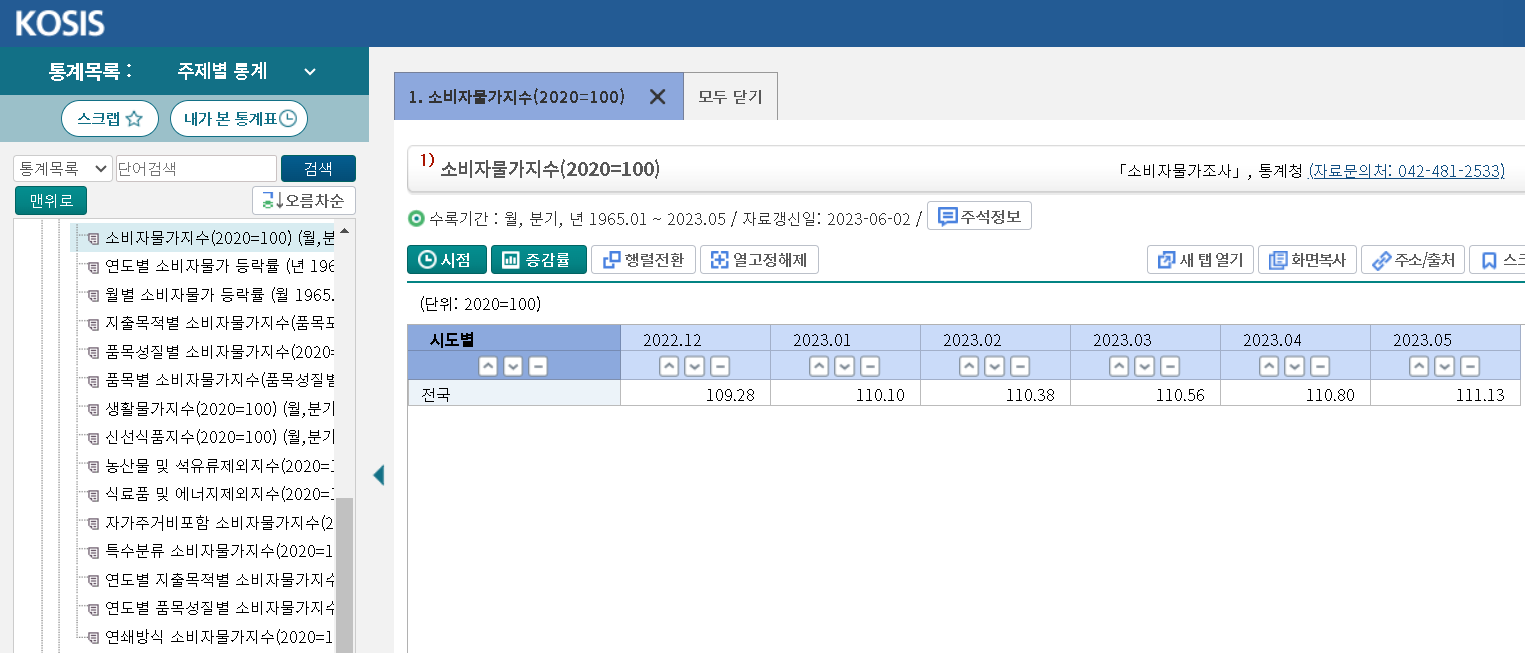
출처:국가통계포털, kosis
인플레이션에 관한 여러 데이터 수집을 위해 국가통계포털을 사용하였고,
M2통화지표, 생산자물가지수, 소비자물가지수, 생필품물가지수, 기준금리, 지가지수, 코스피지수, 금시세의 데이터를 준비했습니다.
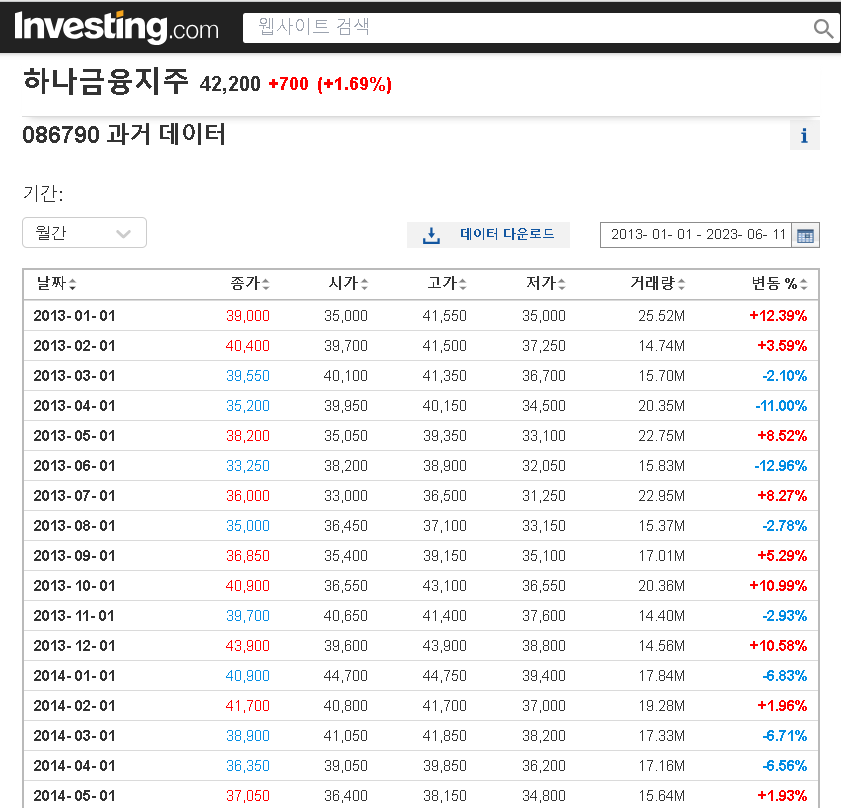
주가에 대한 데이터는 인베스팅닷컴에서 필요한 종목만 csv파일로 다운 받아 사용하였습니다. 나중에 알았지만 크롤링을 사용하여 데이터를 바로 저장할 수 있다는 것은 막바지에 알게 되었는데 후반부에 그것을 사용하여 백테스팅하는 것도 보여줄 것이다.

경제 데이터를 분석하여 인플레이션의 심각성을 시각화하고, 여러 방면의 투자방법을 소개하려 준비하다보니 데이터가 여러가지가 필요했다. 미국주식 한국주식, 주식 가치주, 성장주, 우량주와 같은 섹터별 그래프, 코스피 코스닥 나스닥과 같은 지수별 그래프처럼 분석해보고 시각화해보고 싶은 것이 넘쳐났기에 부푼 기대를 갖고 데이터를 준비했다.
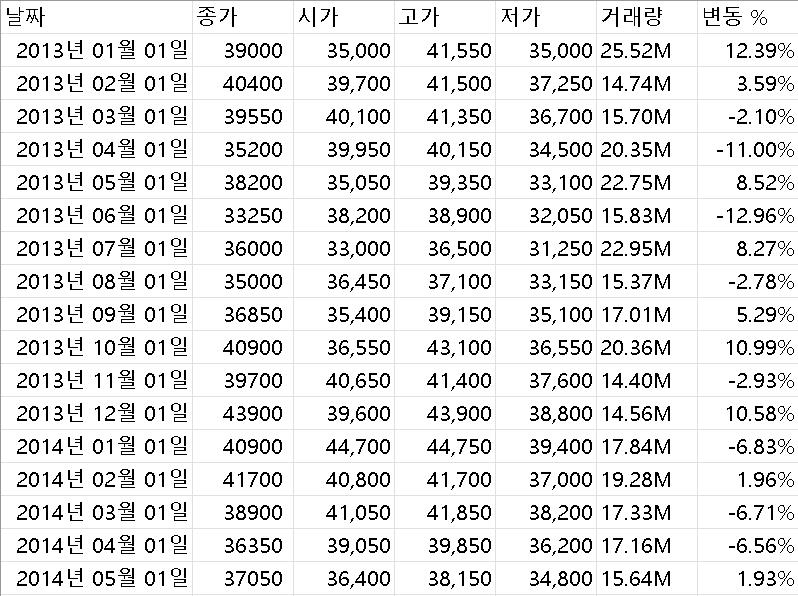
원본데이터 형식은 이와 같았다. 기존과 같은 방법을 사용할 경우 ######으로 되어있던 날짜의 형식을 약간 수정해주었다.
여기서 데이터 종가뿐만 아니라 시가, 종가, 저가, 변동 등 쓰이는 상황이 있기 때문에 따로 데이터 전처리를 해주지는 않았다.
📌인플레이션 지표
이제부터 인플레이션에 관하여 시각화 할 수 있는 지표에 대해 알아보자
📍기준금리 지표
import pandas as pd
# CSV 파일 불러오기
bank_data = pd.read_csv("금리_연별.csv", encoding='cp949') #기준금리
# 선 그래프 작성
plt.plot(bank_data['Date'], bank_data[ 'deposit'], marker='.')
# 그래프 제목과 축 레이블 설정
plt.title('최근 10년간의 금리 변화')
plt.xlabel('연')
plt.ylabel('고정금리')
# x축 눈금 라벨 회전
plt.xticks(rotation=45)
# 그리드
plt.grid(False)
# 그래프 출력
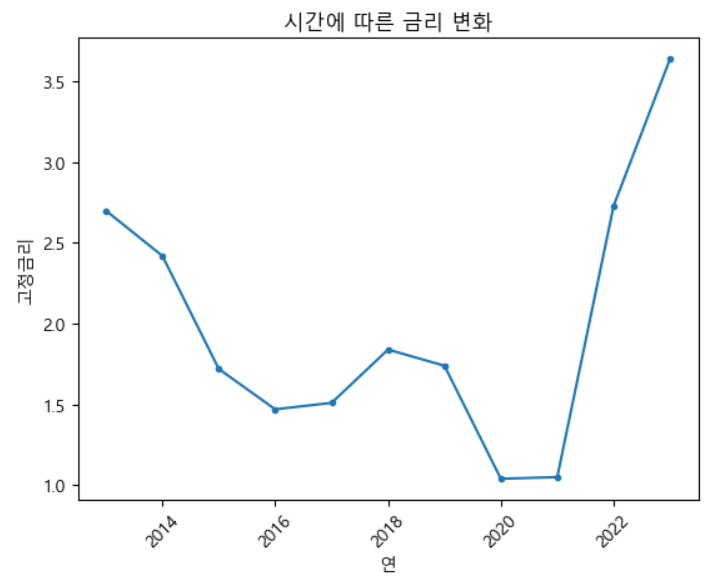
plt.show()인플레이션이 심각하다는 것을 보여주기 위해 인플레이션을 막기위해 요즘 이슈화 되고있는 금리 변화에 대해 시각화하였다.
📍생산자,소비자물가지수
# CSV 파일 불러오기
producer_data = pd.read_csv("생산자물가지수_증감률.csv", encoding='cp949')
Consumer_data = pd.read_csv("소비자물가지수_증감률.csv", encoding='cp949')
# 선 그래프 작성
plt.plot(producer_data['시점'], producer_data['생산자물가지수'],
marker='.', label='생산자물가지수')
plt.plot(Consumer_data['시점'], Consumer_data['소비자물가지수'],
marker='.', label='소비자물가지수')
# 그래프 제목과 축 레이블 설정
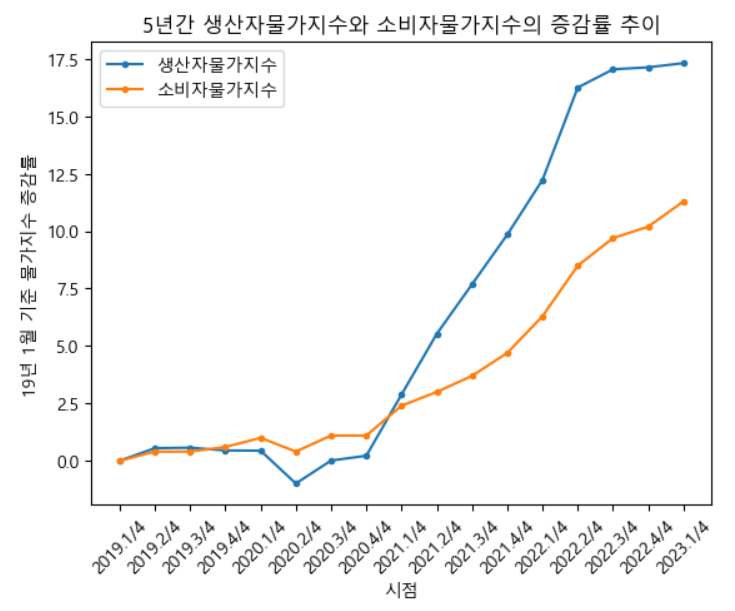
plt.title('5년간 생산자물가지수와 소비자물가지수의 증감률 추이')
plt.xlabel('시점')
plt.ylabel('19년 1월 기준 물가지수 증감률')
# x축 눈금 라벨 회전
plt.xticks(rotation=45)
# 범례 추가
plt.legend()
# 그래프 출력
plt.show()인플레이션을 시각화하기 위해 최근 5년간 생산자물가지수와, 소비자물가지수의 증감률 추이를 2019년 1분기를 기준(0)으로 놓고 지수화하였다.
📍M2통화지표
m2_data = pd.read_csv("통화지표_막대바.csv", encoding='cp949')
# 선 그래프 작성
plt.plot(m2_data['시점'], m2_data['M2'], marker='.', label='M2통화지표')
# 막대 그래프 그리기
plt.bar(m2_data['시점'], m2_data['M2'])
#축 레이블 지정
plt.xlabel('시점')
plt.ylabel('M2통화지표')
# 그래프 제목 설정
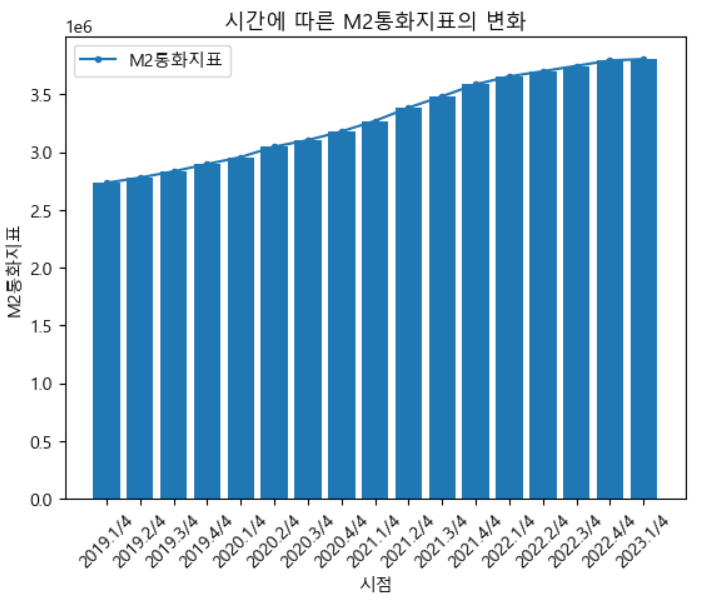
plt.title('시간에 따른 M2통화지표의 변화')
# x축 눈금 라벨 회전
plt.xticks(rotation=45)
# 범례 추가
plt.legend()
# 그래프 보여주기
plt.show()인플레이션을 시각화하기위해 풀려있는 현금유동성지표인 M2통화지표의 변화를 막대그래프와 선그래프를 함께 보여줌으로써 시각화하였습니다.
📍생필품 물가지수
# CSV 파일 불러오기
producer_data = pd.read_csv("생산자물가지수_증감률_품목별.csv", encoding='cp949')
Consumer_data = pd.read_csv("소비자물가지수_증감률_품목별.csv", encoding='cp949')
# 선 그래프 작성
plt.plot(Consumer_data['시점'], Consumer_data['라면'],
marker='.', label='라면')
plt.plot(producer_data['시점'], producer_data['닭고기'],
marker='.', label='닭고기')
plt.plot(Consumer_data['시점'], Consumer_data['전기료'],
marker='.', label='전기료')
plt.plot(Consumer_data['시점'], Consumer_data['도시가스'],
marker='.', label='도시가스')
plt.plot(Consumer_data['시점'], Consumer_data['지역난방비'],
marker='.', label='난방비')
# 그래프 제목과 축 레이블 설정
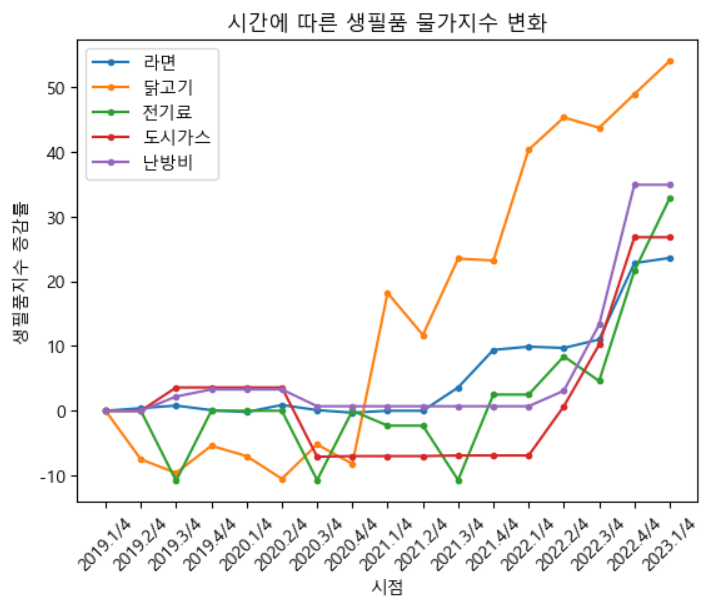
plt.title('시간에 따른 생필품 물가지수 변화')
plt.xlabel('시점')
plt.ylabel('생필품지수 증감률')
# x축 눈금 라벨 회전
plt.xticks(rotation=45)
# 범례 추가
plt.legend()
# 그래프 출력
plt.show()생산자,소비자 물가지수 안에 세부항목으로 생필품 물가지수가 들어있는데 그중에서 대표적인 것을 몇가지를 예로 들어 생필품 가격이 빠르게 상승중이라는 것을 보여주기 위해 시각화하였습니다.
📌투자자산 지표
인플레이션에 대비되어 지난 5년, 10년간 상승하고 있는 여러 투자자산들의 지표를 통해 떨어지는 현금가치를 직접 시각화한다.
📍지가지수 지표
# CSV 파일 불러오기
real_estate_data = pd.read_csv("지가지수.csv", encoding='cp949')
real_estate_data['years'] = pd.to_datetime(real_estate_data['years'], format="%Y")
# 선 그래프 작성
plt.plot(real_estate_data['years'], real_estate_data['an index of land'],
marker='.', label='부동산 지가지수')
# 그래프 제목과 축 레이블 설정
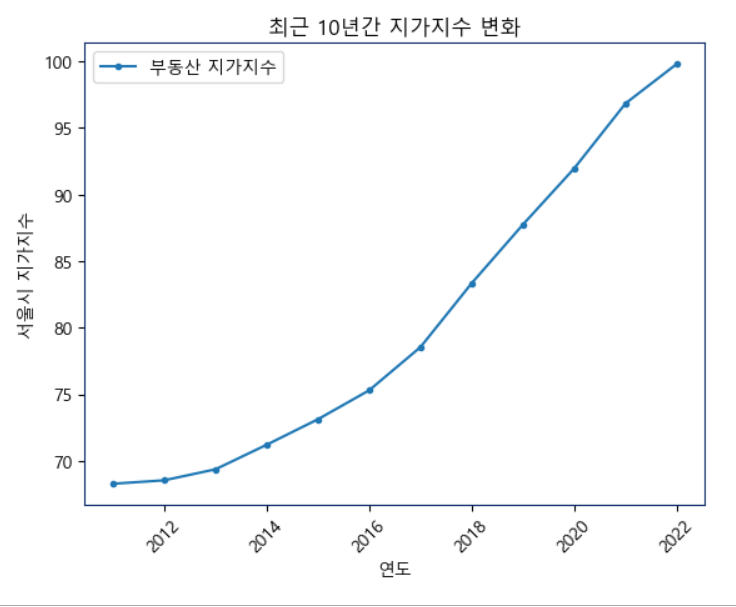
plt.title('최근 10년간 지가지수 변화')
plt.xlabel('연도')
plt.ylabel('서울시 지가지수')
# x축 눈금 라벨 회전
plt.xticks(rotation=45)
# 범례 추가
plt.legend()
# 그리드
plt.grid(False)
# 그래프 출력
plt.show()인플레이션으로 떨어지는 현금가치와 대비하여 올라가는 지가지수를 시각화하였습니다.
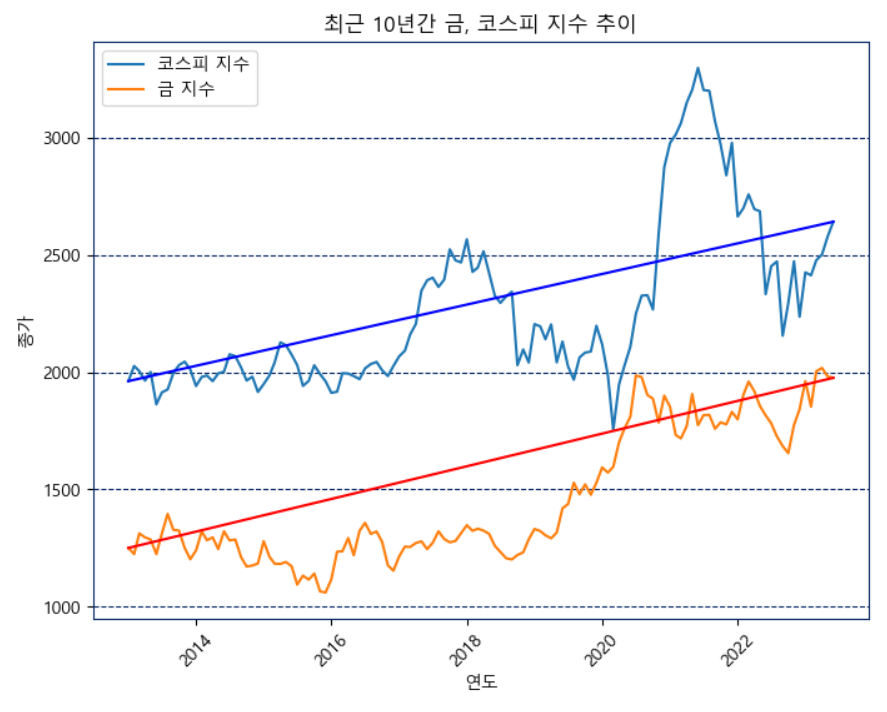
📍금 지수, 코스피 지수 지표
gold_data = pd.read_csv("금_지수.csv", encoding='utf-8')
gold_data['날짜'] = pd.to_datetime(gold_data['날짜'], format="%Y년 %m월 %d일")
kospi_data = pd.read_csv("코스피.csv", encoding='utf-8')
kospi_data['날짜'] = pd.to_datetime(kospi_data['날짜'], format="%Y년 %m월 %d일")
plt.figure(figsize=(8, 6))
# 일봉 선 차트 그리기
plt.plot(kospi_data['날짜'], kospi_data['종가'],
label='코스피 지수')
plt.plot(gold_data['날짜'], gold_data['종가'],
label='금 지수')
# 2013년과 2023년의 데이터 생성
gold_years = [pd.Timestamp('2013-01-01'), pd.Timestamp('2023-06-01')]
gold_values = [1251, 1976]
# 2013년과 2023년의 데이터 생성
kospi_years = [pd.Timestamp('2013-01-01'), pd.Timestamp('2023-06-01')]
kospi_values = [1961.94 , 2641.16 ]
# 2013년과 2023년을 두 점으로 연결하는 직선 그리기
plt.plot(gold_years, gold_values, 'r-')
plt.plot(kospi_years, kospi_values, 'b-')
# 그래프 제목과 축 레이블 설정
plt.title('최근 10년간 금, 코스피 지수 추이')
plt.xlabel('연도')
plt.ylabel('종가')
# x축 눈금 라벨 회전
plt.xticks(rotation=45)
# 범례 추가
plt.legend()
# 격자 추가
plt.grid(False)
# 그리드
plt.grid(True, axis='y')
# 그래프 출력
plt.show()떨어지는 현금가치와 대비하여 올라가는 다른 투자자산들을 시각화하였습니다.
plt.plot(gold_years, gold_values, 'r-')
plt.plot(kospi_years, kospi_values, 'b-')
2013년과 2023년을 두 점으로 연결하는 직선 그리기를 통하여 직선으로 지난 10년간 올랐다는 것을 시각화합니다.
📌인플레이션에 대항하는 투자
고인플레이션 시대에 떨어지는 현금가치를 보전 할 수 있는 투자방법으로 주식투자를 추천해준다. 주식투자의 여러 섹터별 추이를 시각화하여 알려준다.
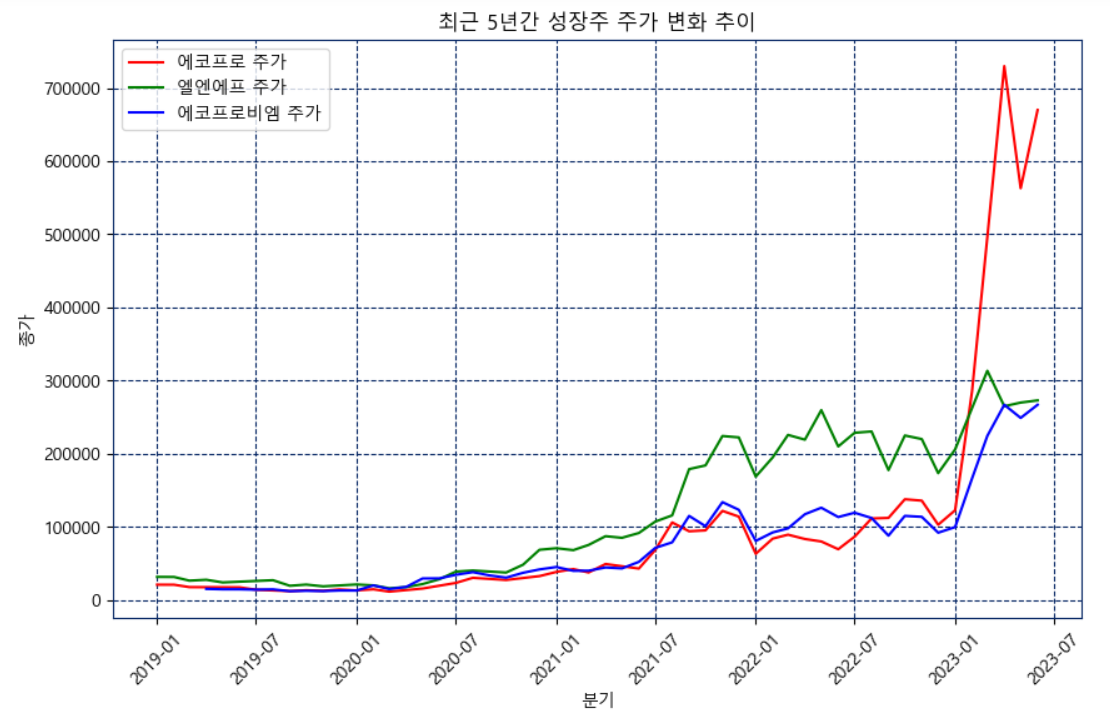
📍성장주 지표
eco_data = pd.read_csv("2차전지_에코프로.csv", encoding='utf-8')
eco_data['날짜'] = pd.to_datetime(eco_data['날짜'], format="%Y년 %m월 %d일")
ln_data = pd.read_csv("2차전지_엘엔에프.csv", encoding='utf-8')
ln_data['날짜'] = pd.to_datetime(ln_data['날짜'], format="%Y년 %m월 %d일")
bm_data = pd.read_csv("2차전지_에코프로비엠.csv", encoding='utf-8')
bm_data['날짜'] = pd.to_datetime(bm_data['날짜'], format="%Y년 %m월 %d일")
# 일봉 선 차트 그리기
plt.figure(figsize=(12, 6))
plt.plot(eco_data['날짜'], eco_data['종가'],
label='에코프로 주가',color='red')
plt.plot(ln_data['날짜'], ln_data['종가'],
label='엘엔에프 주가', color='green')
plt.plot(bm_data['날짜'], bm_data['종가'],
label='에코프로비엠 주가',color='blue')
# 그래프 제목과 축 레이블 설정
plt.title('시간에 따른 성장주 주가 변화 추이')
plt.xlabel('분기')
plt.ylabel('종가')
# x축 눈금 라벨 회전
plt.xticks(rotation=45)
# 범례 추가
plt.legend()
# 격자 추가
#plt.grid()
# 그리드
plt.grid(False)
plt.grid(True, axis='y')
# 그래프 출력
plt.show()2차전지 성장주인 에코프로와 에코프로비엠, 엘엔에프의 주가 추이를 시각화하여 미래 성정가치가 있는 성장할 섹터의 성장성을 시각화한다.
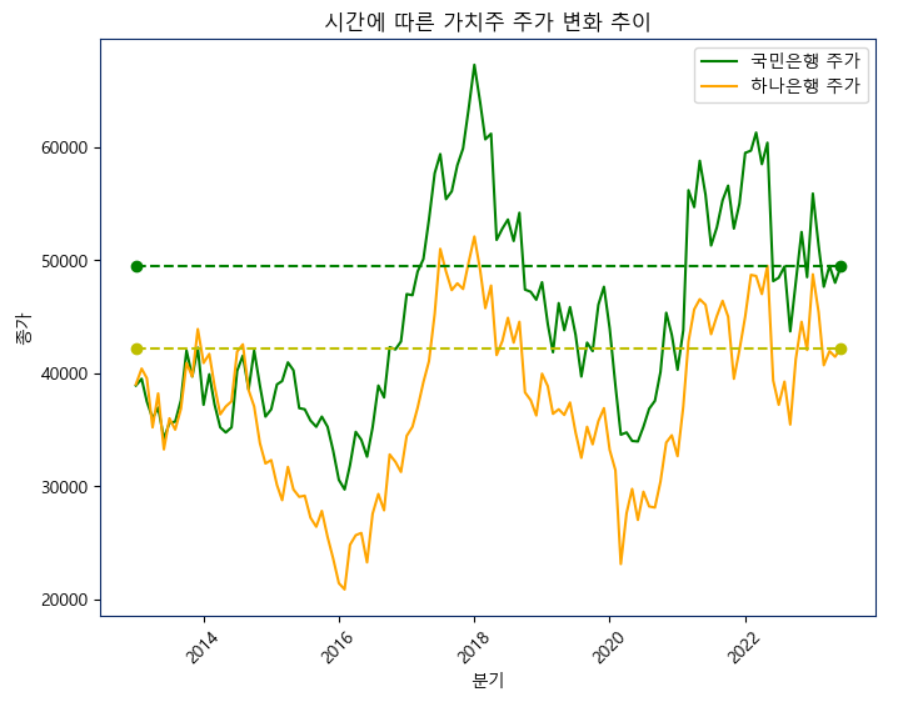
📍가치주 지표
kb_data = pd.read_csv("은행주_국민은행.csv", encoding='utf-8')
kb_data['날짜'] = pd.to_datetime(kb_data['날짜'], format="%Y년 %m월 %d일")
#yh_data = pd.read_csv("은행주_신한은행.csv", encoding='utf-8')
#yh_data['날짜'] = pd.to_datetime(yh_data['날짜'], format="%Y년 %m월 %d일")
hn_data = pd.read_csv("은행주_하나은행.csv", encoding='utf-8')
hn_data['날짜'] = pd.to_datetime(hn_data['날짜'], format="%Y년 %m월 %d일")
# 일봉 선 차트 그리기
plt.figure(figsize=(8, 6))
plt.plot(kb_data['날짜'], kb_data['종가'],
label='국민은행 주가',color='green')
#plt.plot(yh_data['날짜'], yh_data['종가'],
# label='신한은행 주가',color='orange')
plt.plot(hn_data['날짜'], hn_data['종가'],
label='하나은행 주가',color='orange')
# 2013년과 2023년의 데이터 생성
kb_years = [pd.Timestamp('2013-01-01'), pd.Timestamp('2023-06-01')]
kb_values = [49450 , 49450 ]
# 2013년과 2023년의 데이터 생성
hn_years = [pd.Timestamp('2013-01-01'), pd.Timestamp('2023-06-01')]
hn_values = [42200 , 42200 ]
# 2013년과 2023년을 두 점으로 연결하는 직선 그리기
plt.plot(kb_years, kb_values, 'go--')
plt.plot(hn_years, hn_values, 'yo--')
# 그래프 제목과 축 레이블 설정
plt.title('시간에 따른 가치주 주가 변화 추이')
plt.xlabel('분기')
plt.ylabel('종가')
# x축 눈금 라벨 회전
plt.xticks(rotation=45)
# 범례 추가
plt.legend()
# 격자 추가
#plt.grid()
# 그리드
plt.grid(False)
# 그래프 출력
plt.show()지난 10년간 가치주의 변화 추이를 시각화하여 소개한다.
가치주의 특별한점은 흐름을 가지고 성장보다는 흐름을 타는 경향을 보이는데 그것을 더 잘 이해할 수 있도록
# 2013년과 2023년의 데이터 생성
kb_years = [pd.Timestamp('2013-01-01'), pd.Timestamp('2023-06-01')]
kb_values = [49450 , 49450 ]
# 2013년과 2023년의 데이터 생성
hn_years = [pd.Timestamp('2013-01-01'), pd.Timestamp('2023-06-01')]
hn_values = [42200 , 42200 ]
# 2023년을 기준으로 직선 그리기
plt.plot(kb_years, kb_values, 'go--')
plt.plot(hn_years, hn_values, 'yo--')위의 코드처럼 마지막 종가에 가로로 직선을 그어서 10년간 지표를 시각화한다.
사진에서 보면 알 수 있는 것처럼 시간이 지난다고 우상향하는 주식이 아닌 것을 알 수 있다.
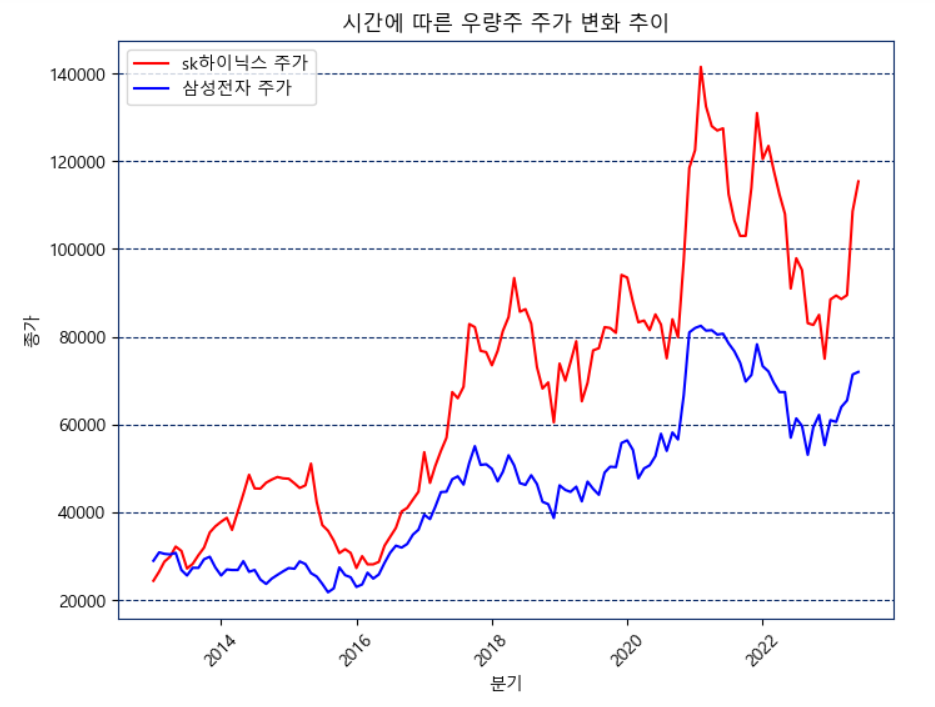
📍우량주 지표
sk_data = pd.read_csv("우량주_sk하이닉스.csv", encoding='utf-8')
sk_data['날짜'] = pd.to_datetime(sk_data['날짜'], format="%Y년 %m월 %d일")
ss_data = pd.read_csv("우량주_삼성전자.csv", encoding='utf-8')
ss_data['날짜'] = pd.to_datetime(ss_data['날짜'], format="%Y년 %m월 %d일")
# 일봉 선 차트 그리기
plt.figure(figsize=(8, 6))
plt.plot(sk_data['날짜'], sk_data['종가'],
label='sk하이닉스 주가',color='red')
plt.plot(ss_data['날짜'], ss_data['종가'],
label='삼성전자 주가',color='blue')
# 그래프 제목과 축 레이블 설정
plt.title('시간에 따른 우량주 주가 변화 추이')
plt.xlabel('분기')
plt.ylabel('종가')
# x축 눈금 라벨 회전
plt.xticks(rotation=45)
# 범례 추가
plt.legend()
# 격자 추가
plt.grid(False)
# 그리드
plt.grid(True, axis='y')
# 그래프 출력
plt.show()우량주 주가 변화추이로 가장 높은 시총을 가지고 있는 삼성전자와 sk하이닉스를 예로 들었다.
시간이 지날수록 우상향하는 것을 볼수 있고 그 그래프가 가파르지 않게 꾸준한 성장을 하는 것 또한 볼 수 있다.
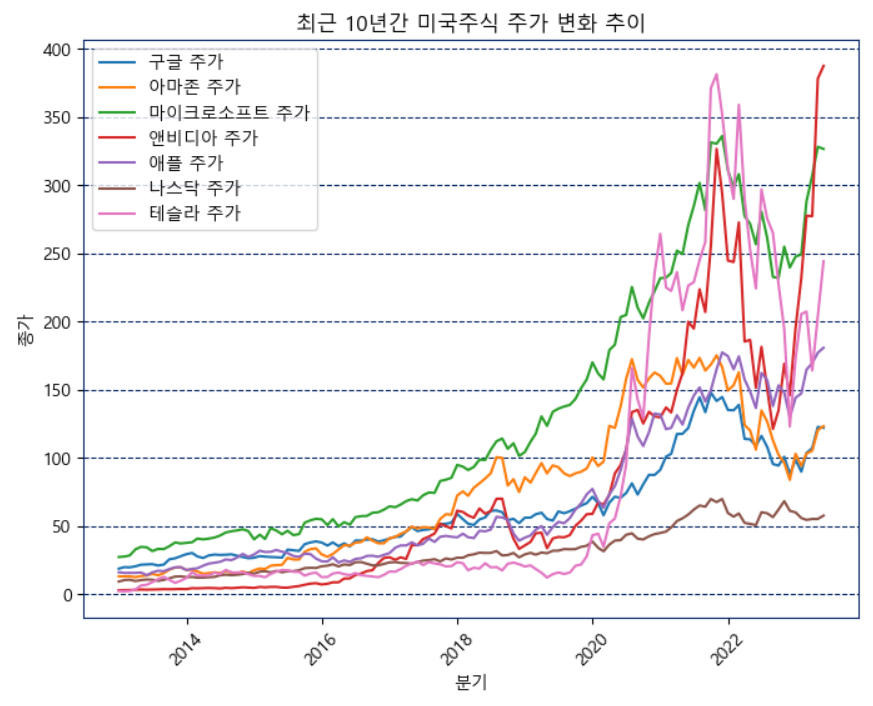
📍미국주식
sk_data = pd.read_csv("나스닥_전체.csv", encoding='utf-8')
sk_data['날짜'] = pd.to_datetime(sk_data['날짜'], format="%Y년 %m월 %d일")
#구글, 아마존, 마이크로소프트, 앤비디아, 애플, 나스닥, 코카콜라, 테슬라
# 일봉 선 차트 그리기
plt.figure(figsize=(8, 6))
plt.plot(sk_data['날짜'], sk_data['구글'],
label='구글 주가')
plt.plot(sk_data['날짜'], sk_data['아마존'],
label='아마존 주가')
plt.plot(sk_data['날짜'], sk_data['마이크로소프트'],
label='마이크로소프트 주가')
plt.plot(sk_data['날짜'], sk_data['앤비디아'],
label='앤비디아 주가')
plt.plot(sk_data['날짜'], sk_data['애플'],
label='애플 주가')
#plt.plot(sk_data['날짜'], sk_data['나스닥'],
# label='나스닥 주가')
#plt.plot(sk_data['날짜'], sk_data['코카콜라'],
# label='코카콜라 주가')
plt.plot(sk_data['날짜'], sk_data['테슬라'],
label='테슬라 주가')
# 그래프 제목과 축 레이블 설정
plt.title('최근 10년간 미국주식 주가 변화 추이')
plt.xlabel('분기')
plt.ylabel('종가')
# x축 눈금 라벨 회전
plt.xticks(rotation=45)
# 범례 추가
plt.legend()
# 격자 추가
#plt.grid()
# 그리드
plt.grid(False)
plt.grid(True, axis='y')
# 그래프 출력
plt.show()미국의 빅테크 주식들의 지난 10년간 변화 추이를 나타낸 그래프이다.
다들 우상향하는 것을 볼 수 있고 이것을 더 잘 나태내기 위해 한꺼번에 시각화하였다.
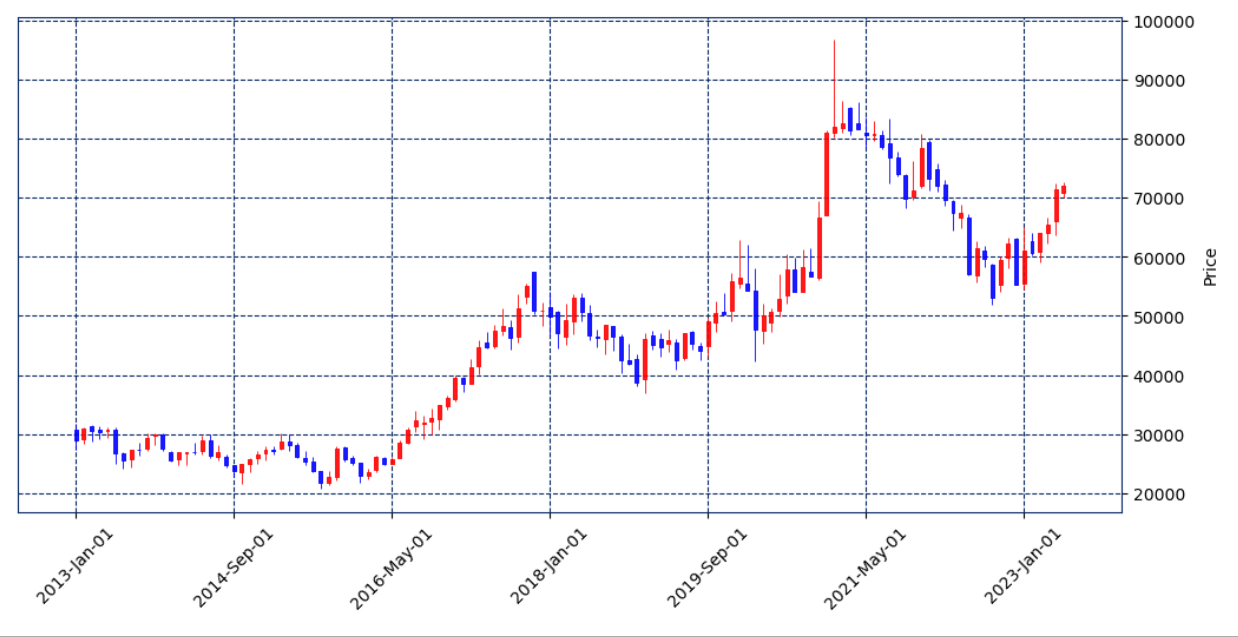
📍mplfinance
- mplfinance를 import하여 캔들차트를 생성해보자
import pandas as pd
import mplfinance as mpf
# CSV 파일 읽기
sk_data = pd.read_csv("코스피지수.csv", encoding='utf-8')
# 열 이름 수정
sk_data.rename(columns={'날짜': 'Date', '시가': 'Open', '고가': 'High', '저가': 'Low',
'종가': 'Close', '거래량': 'Volume', '변동 %': 'Change'}, inplace=True)
# 날짜 열을 Datetime 형식으로 변환
sk_data['Date'] = pd.to_datetime(sk_data['Date'], format="%Y년 %m월 %d일")
# 인덱스를 "Date" 열로 설정
sk_data.set_index('Date', inplace=True)
# 캔들차트 생성
mc = mpf.make_marketcolors(up="r", down="b", edge="inherit", wick="inherit")
s = mpf.make_mpf_style(base_mpf_style="starsandstripes",
marketcolors=mc, gridaxis='both', y_on_right=True)
mpf.plot(sk_data, type='candle', style=s, figsize=(13, 6))
mplfinance는 파이썬의 matplotlib 라이브러리를 기반으로 한 시각화 도구이다. 주로 주식 및 금융 데이터를 시각화하는 데 사용된다.
mplfinance는 주식 차트, 캔들스틱 차트, 볼린저 밴드, 이동평균선, 거래량 등 다양한 테크니컬 지표를 포함한 다양한 종류의 차트를 생성할 수 있다. 이를 통해 트렌드 분석, 패턴 탐지, 거래 신호 등을 시각적으로 확인하는데 사용될 수 있다.
📌투자전략
이제는 주식의 상관성에 관련하여 투자전략을 소개하고 그에 맞게 데이터를 분석하여 타당성을 증명할 것이다.
📍코스피와 삼성전자의 연관
- 먼저 코스피와 삼성전자의 연관성을 알아보자
# CSV 파일 읽기
ss_data = pd.read_csv("우량주_삼성전자.csv", encoding='utf-8')
kospi_data = pd.read_csv("코스피.csv", encoding='utf-8')
# 날짜 열을 Datetime 형식으로 변환
ss_data['날짜'] = pd.to_datetime(ss_data['날짜'], format="%Y년 %m월 %d일")
kospi_data['날짜'] = pd.to_datetime(kospi_data['날짜'], format="%Y년 %m월 %d일")
# 종가 데이터를 담은 열 추출
ss_close = ss_data['종가']
kospi_close = kospi_data['종가']
# 데이터프레임 합치기
merged_data = pd.concat([ss_close, kospi_close], axis=1)
merged_data.columns = ['삼성전자', '코스피']
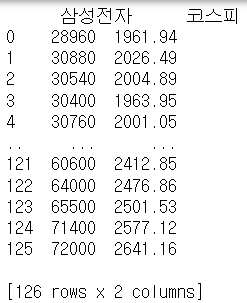
print(merged_data)merged_data = pd.concat([ss_close, kospi_close], axis=1)
merged_data.columns = ['삼성전자', '코스피']코스피.csv와 삼성전자.csv파일을 불러오고, 이중에 각 '종가'열 만을 사용할 것이기에 각 파일에서 종가 열을 데이터 프레임에 할당한다.
데이터프레임을 합친다.
# 산포도 생성
plt.scatter(merged_data['삼성전자'], merged_data['코스피'])
plt.xlabel('삼성전자 종가')
plt.ylabel('코스피 종가')
plt.title('삼성전자 종가와 코스피의 산포도')
# 그리드
plt.grid(False)
#plt.grid(True, axis='y')
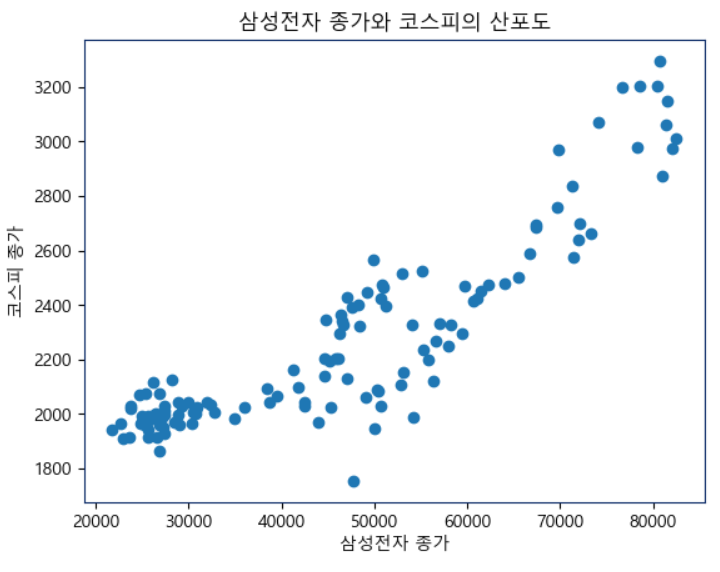
plt.show()코스피와 삼성전자의 값을 산포도로 나타낸다
산포도(Scatter plot)는 두 변수 간의 관계를 나타내기 위해 사용되는 그래프로 양의 값에 일치할 수록 두 변수의 관련성이 높다는 것을 한 눈에 알 수 있다. 뒤에서 일치하지 않는 관계도 표현하겠다.
양의 그래프로 일치하는 것을 볼 수 있다.
# 삼성전자와 코스피 데이텨 지수화
kospi_data['종가 지수화'] = (kospi_data['종가'] / kospi_data['종가'].iloc[0]) * 100
ss_data['종가 지수화'] = (ss_data['종가'] / ss_data['종가'].iloc[0]) * 100
# 그래프 그리기
plt.figure(figsize=(8, 6))
plt.plot(kospi_data['날짜'], kospi_data['종가 지수화'], label='코스피 주가', color='red')
plt.plot(ss_data['날짜'], ss_data['종가 지수화'], label='삼성전자 주가', color='blue')
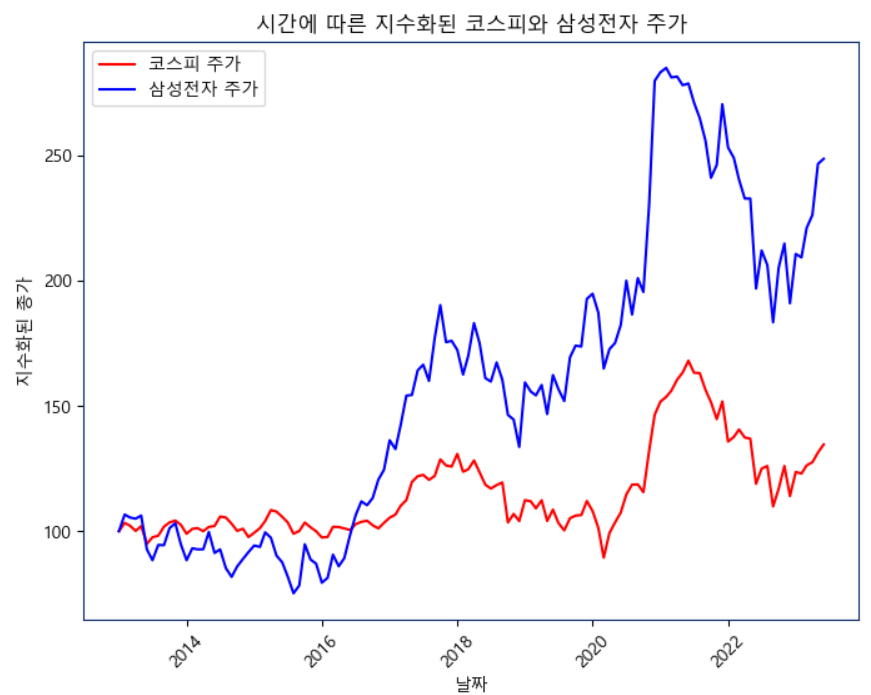
plt.title('시간에 따른 지수화된 코스피와 삼성전자 주가')
plt.xlabel('날짜')
plt.ylabel('지수화된 종가')
plt.xticks(rotation=45)
plt.legend()
plt.grid(False)
plt.show()삼성전자와 코스피 데이터 지수화
kospi_data['종가 지수화'] = (kospi_data['종가'] / kospi_data['종가'].iloc[0]) 100
ss_data['종가 지수화'] = (ss_data['종가'] / ss_data['종가'].iloc[0]) 100
종가' 열을 해당 기간의 초기값으로 나누고, 그 결과에 100을 곱하여 상대적인 변화를 나타내는 '종가 지수화' 열을 생성하여 지수화를 진행한다.
이 작업을 통해 주가의 초기값을 100으로 기준화하여 주가 가격이 다른 주식을 상대적으로 비교하기에 편하다.
지수화 = 종가를 초기값으로 나누고 100을 곱함으로써 초기값을 100으로 만들어준다.
📍환율과 코스피의 연관
# CSV 파일 읽기
hw_data = pd.read_csv("환율.csv", encoding='utf-8')
kospi_data = pd.read_csv("코스피.csv", encoding='utf-8')
# 날짜 열을 Datetime 형식으로 변환
hw_data['날짜'] = pd.to_datetime(hw_data['날짜'], format="%Y년 %m월 %d일")
kospi_data['날짜'] = pd.to_datetime(kospi_data['날짜'], format="%Y년 %m월 %d일")
# 종가 데이터를 담은 열 추출
hw_close = hw_data['종가']
kospi_close = kospi_data['종가']
# 데이터프레임 합치기
merged_data = pd.concat([hw_close, kospi_close], axis=1)
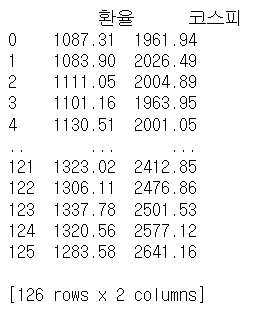
merged_data.columns = ['환율', '코스피']
print(merged_data)이번엔 같은 방법으로 환율과 코스피의 관계를 통해 두 지수의 연관성을 표현해보자
각 데이터의 종가를 추출하여 데이터프레임에 담는다.
# 산포도 생성
plt.scatter(merged_data['환율'], merged_data['코스피'])
plt.xlabel('환율')
plt.ylabel('코스피 종가')
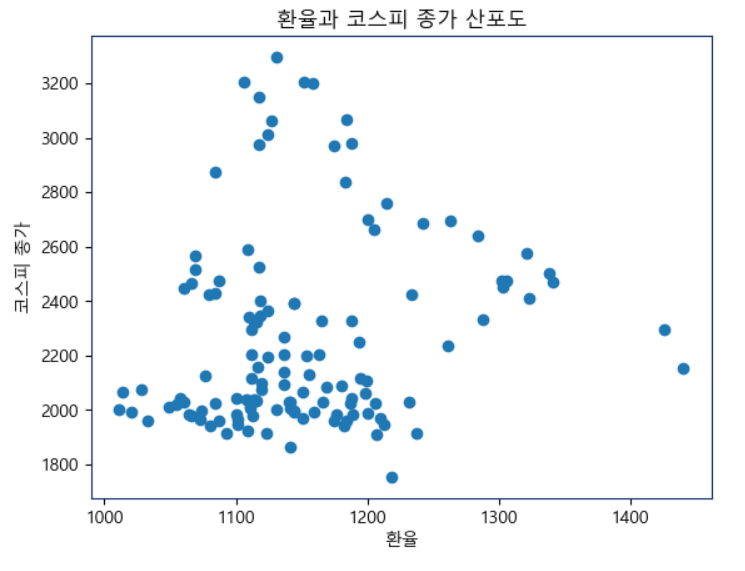
plt.title('환율과 코스피 종가 산포도')
plt.grid(False)
plt.show()산포도로 생성해보자.
이 경우엔 코스피-삼성전자와 반대로 양의 값에 많은 값들이 벗어난 것으로 볼 수 있다. 이 경우엔 일치하는 것이 대체적으로 없다고 볼 수 있다.
그렇다면 그래프로 나타냈을 경우 어떨까
# 데이터 지수화
sk_data['종가 지수화'] = (sk_data['종가'] / sk_data['종가'].iloc[0]) * 100
ss_data['종가 지수화'] = (ss_data['종가'] / ss_data['종가'].iloc[0]) * 100
# 그래프 그리기
plt.figure(figsize=(8, 6))
plt.plot(sk_data['날짜'], sk_data['종가 지수화'], label='환율 주가', color='red')
plt.plot(ss_data['날짜'], ss_data['종가 지수화'], label='코스피 주가', color='blue')
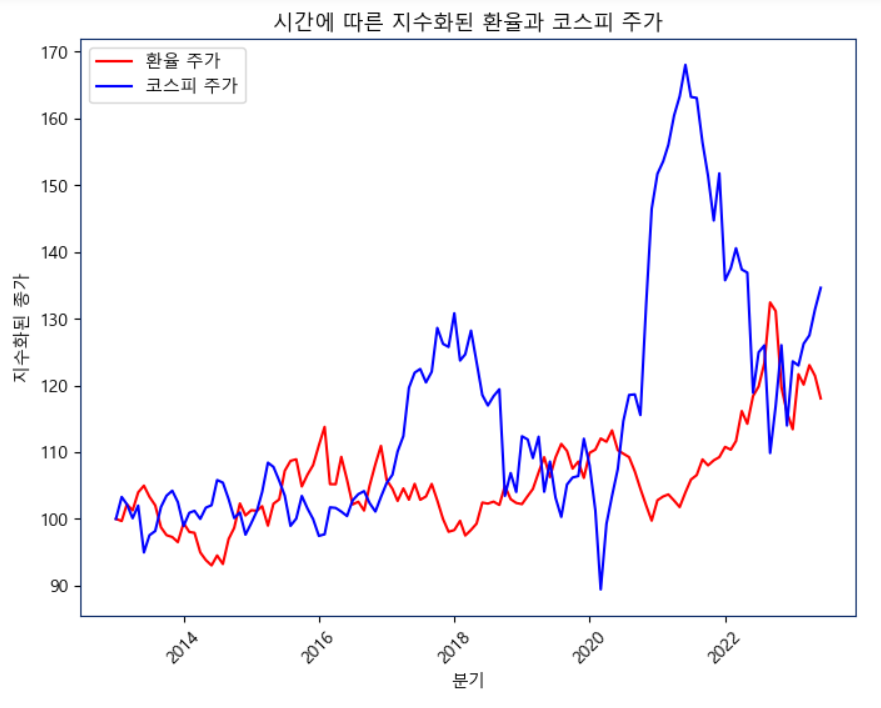
plt.title('시간에 따른 지수화된 환율과 코스피 주가')
plt.xlabel('분기')
plt.ylabel('지수화된 종가')
plt.xticks(rotation=45)
plt.legend()
plt.grid(False)
#plt.grid(True, axis='x')
plt.show()위와 같은 방법으로 지수화를 거친 후 선 그래프로 출력하였다.
여기서 다른 점은 두 선그래프가 반대로 흘러간다는 것을 볼 수 있다.
환율이 오르면 코스피가 내려가고 환율이 내려갈 경우 코스피가 상승한다.
음의 관계를 지닌다는 것을 확인 할 수가 있다.
🧛♂️할로윈 투자 전략
- 11월에 사서 다음 연도 4월에 매도하는 할로윈 투자 전략에 대해 알아보자
📍FinanceDataReader
- 금융 데이터 수집 라이브러리인 FinanceDataReader를 사용하여 주식 데이터를 수집할 수 있었다. 코스피 데이터를 수집하고 2000년도부터 현재까지 데이터를 수집하였다.
import FinanceDataReader as fdr
kospi = fdr.DataReader('KS11', '2000')
# 비어 있는 행 삭제
kospi = kospi.dropna()
for year in range(2000, 2023):
매수_달 = str(year) + '-11'
매도_달 = str(year+1) + '-04'
누적수익률 = 1.0
for year in range(2000, 2023):
매수_달 = str(year) + '-11'
매도_달 = str(year+1) + '-04'
매수가 = kospi.loc[매수_달].iloc[0]['Open'] # 11월 첫 거래일 시가
매도가 = kospi.loc[매도_달].iloc[-1]['Close'] # 4월 마지막 거래일 종가
수익률 = 매도가/매수가
누적수익률 = 누적수익률 * 수익률
print(누적수익률)2000년 - 2023년 까지의 데이터를 11월과 04월로 분류한다.
11월 첫 거래일 시가 기준으로 매수할텐데 loc[]를 사용하여 행을 분류하고 iloc로 시가을 정의한다.
매도가 역시 같은 방법으로 4월의 마지막 거래일의 종가를 정의한다.
그리고 수익률을 구하고 누적 수익률을 구한다.
이 경우에 6.071849277501086라는 수익이나오는데
이는 6배에 달하는 수익이다.
📍결측치 제거

- 여기서 처음에 값이 안 나와서 많이 시간을 소비했다. 이유를 찾으려 각 연도별로 뜯어보고 월별로 뜯어봤는데 nan이라는 결측값이 나오기 때문이었다.
원본 데이터에 빈 행이 존재하는데 그 곳에 거래 시작일이나 거래 종료일이 걸릴 경우 결측값 때문에 nan으로 출력되는 현상이었다.
이를 고치려고 여러 방법을 고안하던 중
kospi = kospi.dropna()결측지 제거 코드를 사용하여 고칠 수 있었다.
#열의 이름을 바꾸고, 데이터프레임화
results_df = pd.DataFrame(results, columns=['연도', '주식수익률'])
# 막대 그래프 생성
colors = ['r' if x >= 0 else 'b' for x in results_df['주식수익률']]
plt.bar(results_df['연도'], results_df['주식수익률'], color=colors)
plt.xlabel('연도')
plt.ylabel('주식수익률')
plt.title('연도별 주식 수익률')
plt.xticks(rotation=45)
plt.grid(False)
plt.grid(True, axis='y')
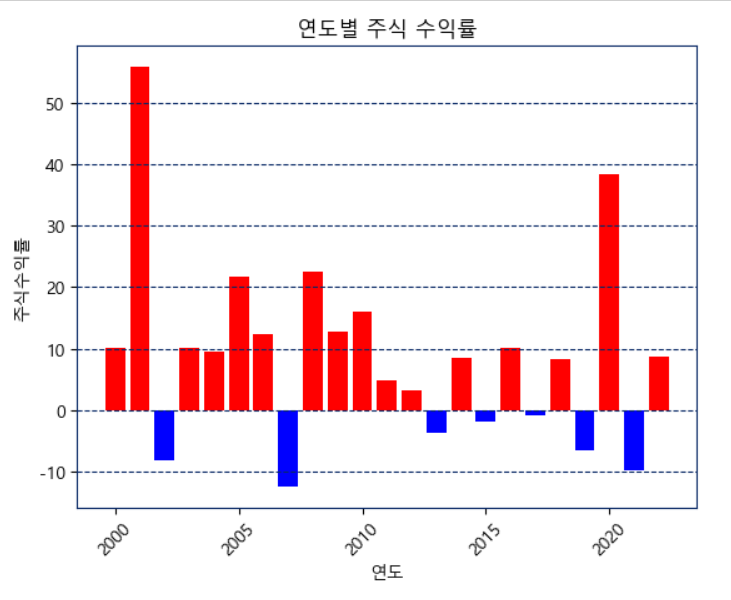
plt.show()누적 수익률에 모두 곱해줬다면 이번엔 각 연도별 누적 수익률을 막대그래프로 시각화하였다.
colors = ['r' if x >= 0 else 'b' for x in results_df['주식수익률']]
막대그래프가 0이상일 경우 빨강으로, 0보다 작을 경우 파랑으로 표시하여 시각화를 진행했다.
결과에서 볼 수 있듯이 성공률이 매우 높고 수익률 또한 높은 것을 볼 수 있다.
📍백테스팅 기법
백테스팅(Backtesting)이란?
금융 분야에서 사용되는 트레이딩 전략이나 투자 전략을 과거의 데이터에 적용하여 성과를 평가하는 기법이다.
백테스팅은 트레이딩 전략의 유효성과 효과를 평가하고, 투자 의사 결정을 지원하는 도구로 사용된다.
여기서는 할로윈 투자전략을 과거데이터에 적용하여 얼마나 성과가 있었는지 나타내고, 다른 월에 똑같이 투자했을 경우와 비교하여 얼마나 성과가 있는지를 분석하여 증명하고 시각화할 것이다.
import FinanceDataReader as fdr
kospi = fdr.DataReader('KS11', '2000')
# 비어 있는 행 삭제
kospi = kospi.dropna()
#############################################################
def 투자6개월(df, 시작년=2000, 종료년=2023, 매수월=11):
매도월 = 매수월 + 5
if 매도월 > 12:
매도월 = 매도월 - 12 #12월이 넘어가면 1월로!
누적수익률 = 1.0
for year in range(시작년, 종료년):#2000-2023
매수년 = year
if 매수월 >=8 :#8월이상이 매수월이면 내년으로!
매도년 = 매수년 + 1
else:
매도년 = 매수년#그렇지않으면 이번년에 팜
buy_month = str(매수년) + '-' + str(매수월)
sell_month = str(매도년) + '-' + str(매도월)
#매수월 첫날의 시작가격, 매도월 끝날의 종료가격
매수가 = df.loc[buy_month].iloc[0]['Open']
매도가 = df.loc[sell_month].iloc[-1]['Close']
수익률 = 매도가 / 매수가 # 1.1
누적수익률 = 누적수익률 * 수익률
return 누적수익률
for month in range(1, 13): #1-12월
수익률 = 투자6개월(kospi, 시작년=2000, 종료년=2023, 매수월=month)
plt.bar(month, 수익률)
# 레이블과 제목 추가
plt.xlabel('월')
plt.ylabel('누적 수익률')
plt.title('6개월 투자의 누적 수익률')
# 그리드 설정 (y축만 적용)
plt.grid(axis='x')
# 그래프 보여주기
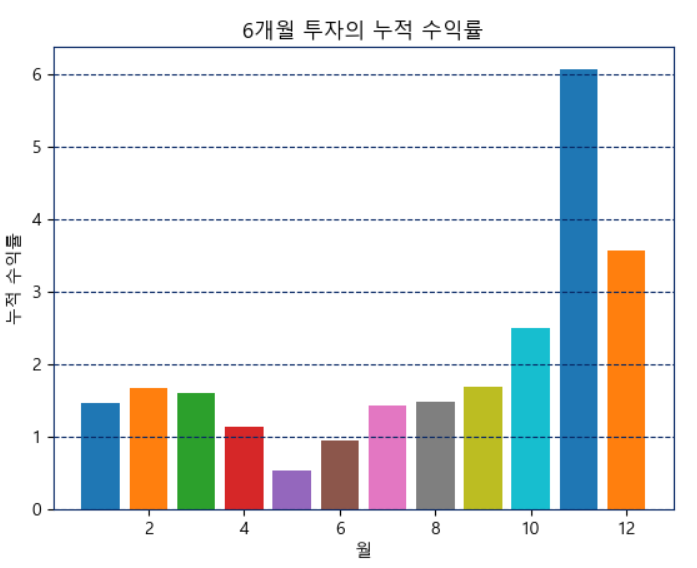
plt.show()1월부터 12월까지 각 월마다 거래시작일에 매수를 진행하고 6개월 후 마지막 거래일에 매도를 진행하였을 경우 수익률을 2000년부터 2023년까지 누적 수익률로 계산하였을 때 과연 11월에 매수를 진행하는 할로윈 투자전략이 얼마나 성과를 거두었는지 백테스팅 기법을 사용하여 알아보았다.
6개월 투자 누적 수익률을 다른 월 보다 11월에 월등히 많았으며 11월 투자의 정반대인 5월에는 수익률이 가장 낮은 것 또한 볼 수 있었다.
이로써 할로윈투자전략을 데이터 분석을 통해 여러 방면에서 성공률이 높고 수익률이 높으며 다른 월에 투자하는 것보다 효율적이라는 결론이 나왔다.


데이터분석 프로젝트 감사하게 잘 보았습니다.
미세먼지 데이터 분석은 자료를 구해서 잘 구현했는데 경제데이터에 대한 파일은 함께 첨부하여 주시면 좋겠습니다.