1. 과대 적합 및 과소 적합에 대한 이해
1) 아이디어
지난 포스팅에서 설계한 다항 선형 회귀 모델의 과소 적합 문제를 해결해보자. 문제를 해결하려면 과대 적합과 과소 적합이 왜 발생하는지부터 명확히 알아야 한다.
먼저 과대 적합은, 모델이 훈련 Set을 너무 잘 학습한 나머지, 훈련 Set에 특화된 패턴(Noise)까지 과반영하면서 발생하는 현상이다. 즉, 일반화 성능이 약하기 때문에 임의로 주어지는 테스트 Set에서 높은 점수를 받지 못하는 것이다. 바로 이와 같은 상황을 가리켜 "모델이 너무 복잡하다"라고 말한다. 따라서, 이 문제를 해결하기 위해선 모델을 더 단순하게 만들어야 할 필요가 있다.
반대로 과소 적합은, 모델이 훈련 Set의 패턴을 제대로 학습하지 못했기 때문에 발생하는 현상이다. 즉, 모델이 너무 단순해서 훈련 Set의 패턴을 자세히 포착하지 못하고 있는 것이다. 이러한 모델은 독립 변수와 종속 변수 간의 관계를 제대로 파악하지 못하고 있을 가능성이 높다. 그러므로 이 문제를 해결하기 위해선 모델을 더 복잡하게 만들어야 할 필요가 있다.
사실 우리가 예전에 KNN 회귀 모델의 K 값을 줄임으로써 과소 적합 문제를 해결할 때에도, 이와 동일한 원리가 적용되어 있었다. 즉, KNN 알고리즘에서는 K 값이 작아질수록 모델이 복잡해진다. 다시 말해, 모델이 복잡하다는 말은 곧, 모델이 훈련 Set의 국지적인 변화에도 민감하게 반응한다는 의미인 것이다.
그렇다면 선형 회귀 모델의 과소 적합 문제는 어떻게 해결할 수 있을까? 우리는 이미 방법을 알고 있다. 모델을 더욱 복잡하게 만들면 된다. 지난 모델은 길이라는 하나의 특성만을 사용하여 회귀 모델을 훈련시켰다. 그러므로, 2가지 이상의 특성을 사용하여 회귀 모델을 훈련시키면, 문제가 해결될 것으로 판단된다.
2) Multiple Regression
두 가지 이상의 특성을 사용하는 선형 회귀를 Multiple Regression(다중 회귀)이라 한다. 특성이 하나였을 때에는 회귀 모델이 2차원 평면에 나타나는 직선(그래프)을 학습했지만, 특성이 2개가 되면 3차원 공간에 나타나는 평면을 학습한다. 종속 변수를 z, 특성 1과 2를 각각 x, y라 하면, 모델이 학습하는 평면의 방정식은 z = ax + by + c의 꼴로 나타날 것이다.
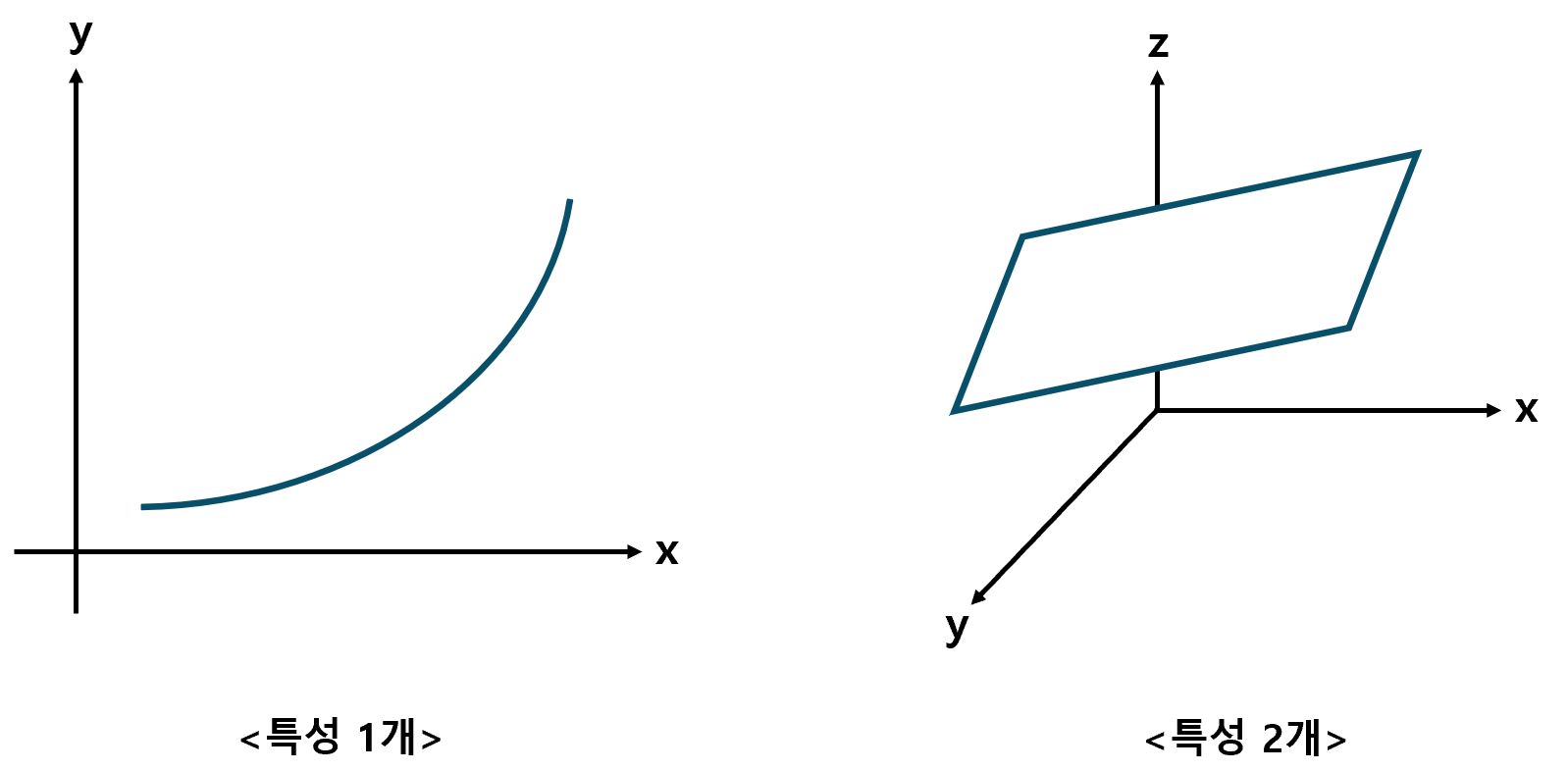
이렇듯 독립 변수가 하나씩 늘어날 때마다 차원도 하나씩 증가한다. 그렇다면, 특성이 3개가 되면 어떻게 될까? 아쉽게도 4차원 이상의 공간은 표현할 수 없기 때문에, 이를 그림으로 나타내기는 어렵다. 하지만, 수학적으로 차원을 무한히 확장하는 것은 가능하기 때문에 특성이 3개 이상이 되더라도, 선형 회귀 모델을 학습시키는 일에는 전혀 문제가 되지 않는다.
이번 포스팅에서는 길이 데이터와 더불어 높이와 두께 데이터도 함께 사용할 예정이다. 새로운 데이터가 추가됨에 따라, 길이와 높이를 곱하여 새로운 특성을 만드는 일도 가능해졌다. 이와 같이 기존 특성을 활용하여 새로운 특성을 만들어내는 작업을 Feature Engineering(특성 공학)이라 한다.
2. Pandas
1) 개념
지금까지는 특성 데이터를 복사 붙여넣기하는 방식으로 데이터 Set을 사용하였다. 그러나 상황에 따라 데이터 Set을 인터넷에서 바로 다운로드하여 사용하는 것이 더 편할 수도 있다.
이 때, 사용할 수 있는 라이브러리가 바로 Pandas이다. Pandas는 데이터분석 라이브러리로, 주요 데이터 구조로 Dataframe을 사용한다. Dataframe은 Numpy 배열처럼 다차원 배열을 손쉽게 조작할 수 있게 해주면서, Numpy에서 제공하지 않는 다양한 추가 기능까지 제공한다. 물론, Dataframe을 Numpy 배열로 변환하는 것도 가능하다.
즉, Pandas 라이브러리를 통해 인터넷의 데이터를 다운로드 받아 Dataframe에 저장한 후, 이를 Numpy 배열로 변환하여 다중 회귀 모델을 훈련시키면 되는 것이다.
2) 데이터 Set 준비하기
Dataframe을 만들기 위해 주로 사용되는 파일 형식은 CSV(Comma-Separated Values)이다. 실습에 사용될 CSV 파일의 내용은 아래와 같다.
>> CSV 파일
Pandas에서 파일을 읽으려면 read_csv()에 파일의 주소를 전달하면 되고, Dataframe을 Numpy 배열로 변환하려면 to_numpy() 메서드를 사용하면 된다.
import pandas as pd
df = pd.read_csv('http://bit.ly/perch_csv_data')
perch_all = df.to_numpy()이로써, 각 Sample의 length, height, width 데이터 준비가 완료되었다. 타깃 데이터(weight)는 기존 방식과 동일하게 복사 붙여넣기 방식으로 준비하고, 훈련 Set과 테스트 Set을 구분해보자.
import numpy as np
from sklearn.model_selection import train_test_split
...
perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0,
115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0,
150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,
218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0,
556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0,
850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0,
1000.0])
...
train_input, test_input, train_target, test_target = train_test_split(perch_all, perch_weight, random_state=42) 3. 사이킷런 Transforemr
1) 개념
지난 포스팅에서 선형 회귀를 다룰 때, 직선 그래프가 추세를 충분히 반영하지 못하기 때문에 길이² 항을 추가하여 곡선 그래프로 나타내었다. 마찬가지로 다중 회귀에서도, 평면이 추세를 충분히 반영하지 못하는 경우, 제곱 항을 추가하여 곡면을 나타내야 할 수 있다.
이를 위해 x, y, z를 각각 제곱하거나, 각 항끼리의 곱을 구해 새로운 항을 만들어야 할 필요가 있다. 사이킷런은 특성을 새로 만들거나, 전처리하기 위한 다양한 클래스를 제공한다. 이러한 클래스를 Transforemr(변환기)라고 한다. 참고로, LinearRegression이나 KNeighborsClassifier와 같은 클래스는 Estimator(추정기)라고 부른다.
여기서 사용할 변환기는 PolynomialFeatures 클래스이다. 먼저 fit() 메서드를 통해 특성 데이터에서 가능한 변환 조합을 찾은 후, transformer() 메서드를 통해 찾은 조합을 실제로 추가한다. 주의해야 할 것은 transformer() 메서드는 변환만 가능하기 때문에, 반드시 호출 전에 fit() 메서드가 선행되어야 한다는 것이다.
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures()
poly.fit([[2, 3]])
print(poly.transform([[2, 3]])) # [[1. 2. 3. 4. 6. 9.]] 출력출력된 결과를 보면, 기존에 있던 2와 3에 2², 2 * 3, 3² 항이 추가된 것을 확인할 수 있다. 참고로, 1은 상수항에 곱해지는 값으로써 추가된 것이므로 무시해도 무방하다.
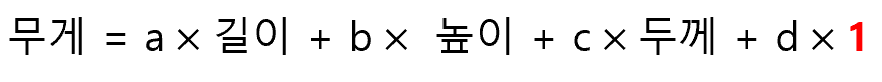
만약 1이 추가되지 않기를 원한다면, include_bias=False로 지정하면 된다. (사이킷런 모델은 자동으로 추가된 절편 항을 무시하기 때문에 include_bias=False를 지정하지 않아도 된다.)
poly = PolynomialFeatures(include_bias=False)
...2) 훈련 데이터 변환하기
사이킷런 Transforemr을 이용하여 train_input을 변환해보자.
poly = PolynomialFeatures(include_bias=False)
poly.fit(train_input)
train_poly = poly.transform(train_input)
print(train_poly.shape) # (42, 9) 출력행이 42개인 이유는 Pandas로 불러온 56개의 데이터 Set 중 75%만 훈련 Set에 포함되었기 때문이다. 열의 개수는 9가 출력되었는데, 9개의 열이 각각 어떤 값을 의미하는지 알아보려면, get_feature_names_out 메서드를 사용하면 된다.
poly.get_feature_names_out()
각 항끼리 곱한 항과 제곱항이 잘 추가된 모습이다. 마찬가지 방법으로 테스트 Set도 변환해주자. 테스트 Set을 변환할 때에도, 훈련 Set을 학습한 변환기를 그대로 사용한다. (별도의 변환기를 만들 수도 있겠지만, 훈련 Set을 기준으로 테스트 Set을 변환할 것을 권장한다.)
test_poly = poly.transform(test_input)4. Regularization
1) 필요성
완성된 훈련 Set과 테스트 Set을 이용하여 모델을 훈련시킨 후, 모델의 성능을 평가해보자.
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))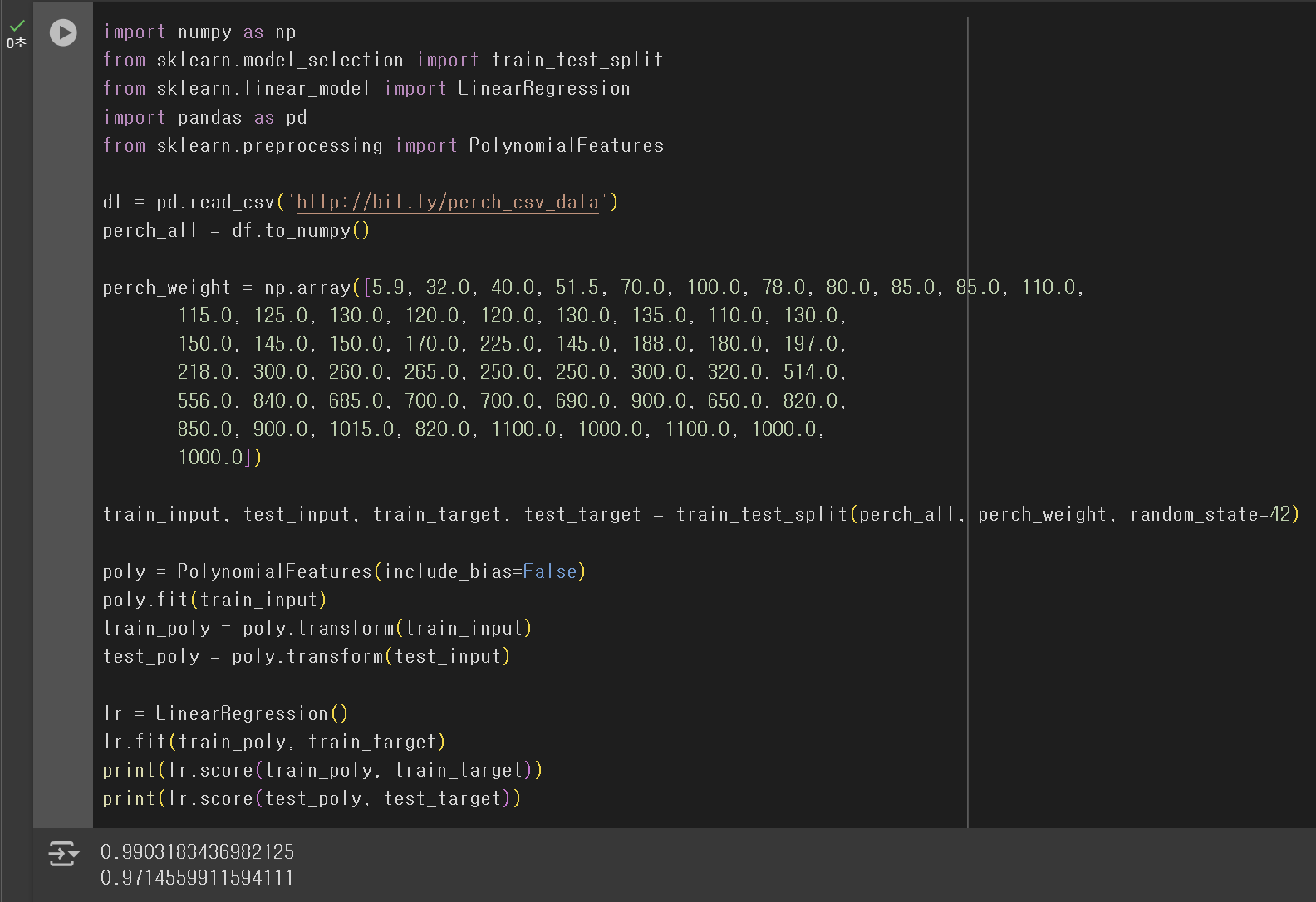
훈련 Set에서의 점수가 크게 상승한 것을 확인할 수 있다. 이 점수는 지난 포스팅에서 설계한 다항 회귀 모델의 점수 0.97보다 높은 수치이다. 이 사실을 통해 알 수 있듯, 특성의 개수가 늘어날수록 모델이 훈련 Set을 더 잘 학습하게 된다. 그렇다면, 더 많은 특성 데이터를 추가함으로써, 더 좋은 모델을 만들 수도 있지 않을까?
이번에는 제곱항뿐 아니라, 3제곱항과 4제곱항, 5제곱항까지 추가해보도록 하겠다. PolynomialFratures 클래스의 degree 값을 변경하면, 최고차항의 차수를 조절할 수 있다.
poly = PolynomialFeatures(degree=5, include_bias=False)
poly.fit(train_input)
train_poly = poly.transform(train_input)
test_poly = poly.transform(test_input)
print(train_poly.shape)
poly.get_feature_names_out()
열의 개수가 무려 55개가 되었다. 참고로, 열의 개수가 55로 계산된 이유는 아래와 같다.

이제 5차항까지 고려한 데이터를 이용해, 모델의 성능을 다시 평가해보자.
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))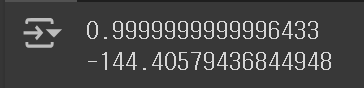
훈련 Set에서는 거의 100에 가까운 점수가 나온 반면, 테스트 Set에서는 터무니 없이 낮은 점수가 나왔다. 이러한 문제가 발생한 이유가 무엇일까? 그 이유는 특성의 개수가 많아짐에 따라, 모델이 너무 복잡해지면서 과대 적합이 발생했기 때문이다. 즉, 훈련 Set의 국지적인 패턴에 민감하게 반응함으로 인해 일반화 성능이 떨어진 것이다.
훈련 Set에 대한 학습도를 낮추기 위해 특성의 개수를 줄일 수도 있겠지만, 특성의 개수를 줄여버리면 지난 포스팅에서 설계한 모델과 다를 바가 없다. 따라서, 이번에는 모델의 복잡성(다양한 특성)은 유지하면서 Regularization(규제)을 활용하여 과대 적합을 해결해보기로 하자.
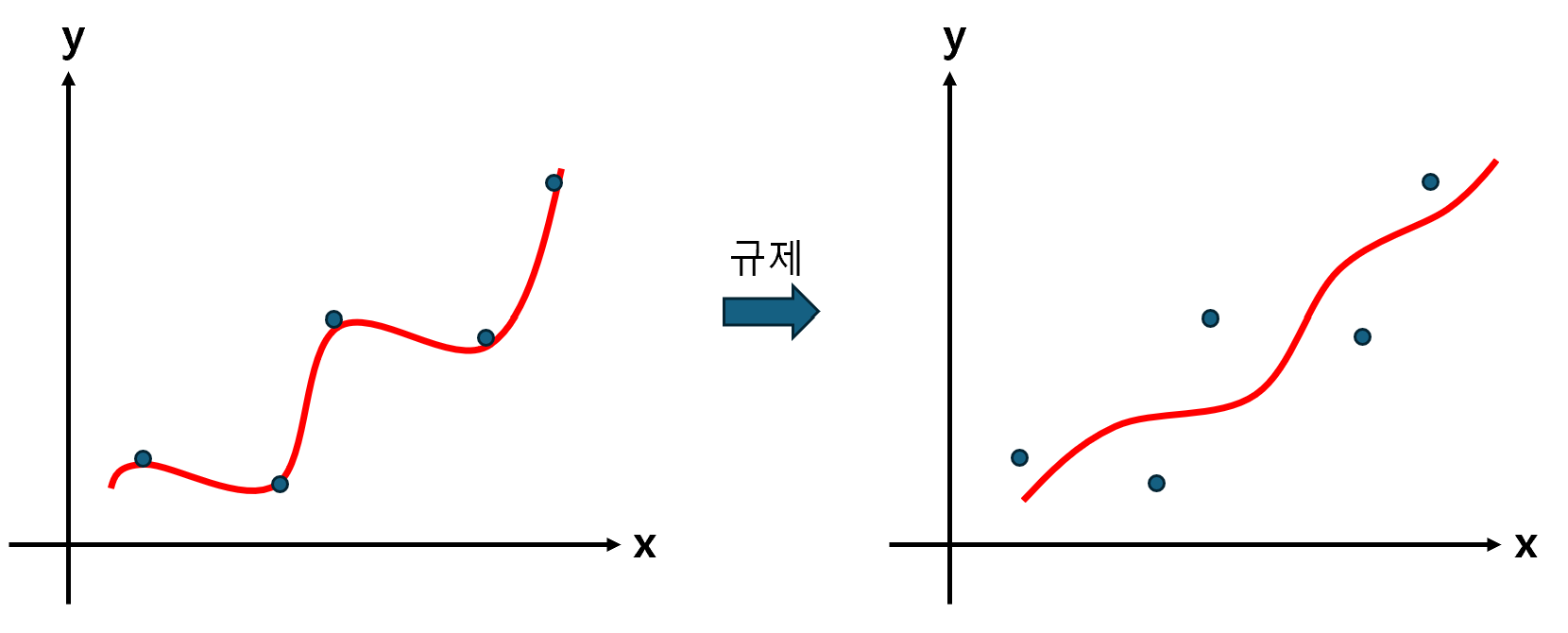
여기서 Regularization이란, 모델이 훈련 Set을 과도하게 학습하지 못하도록 막는 작업으로, 과대 적합을 예방하는 효과가 있다. 선형 회귀 모델을 규제하는 방법은, 그래프의 기울기를 보다 완만하게 만드는 것이다. 아래의 그림을 보자.
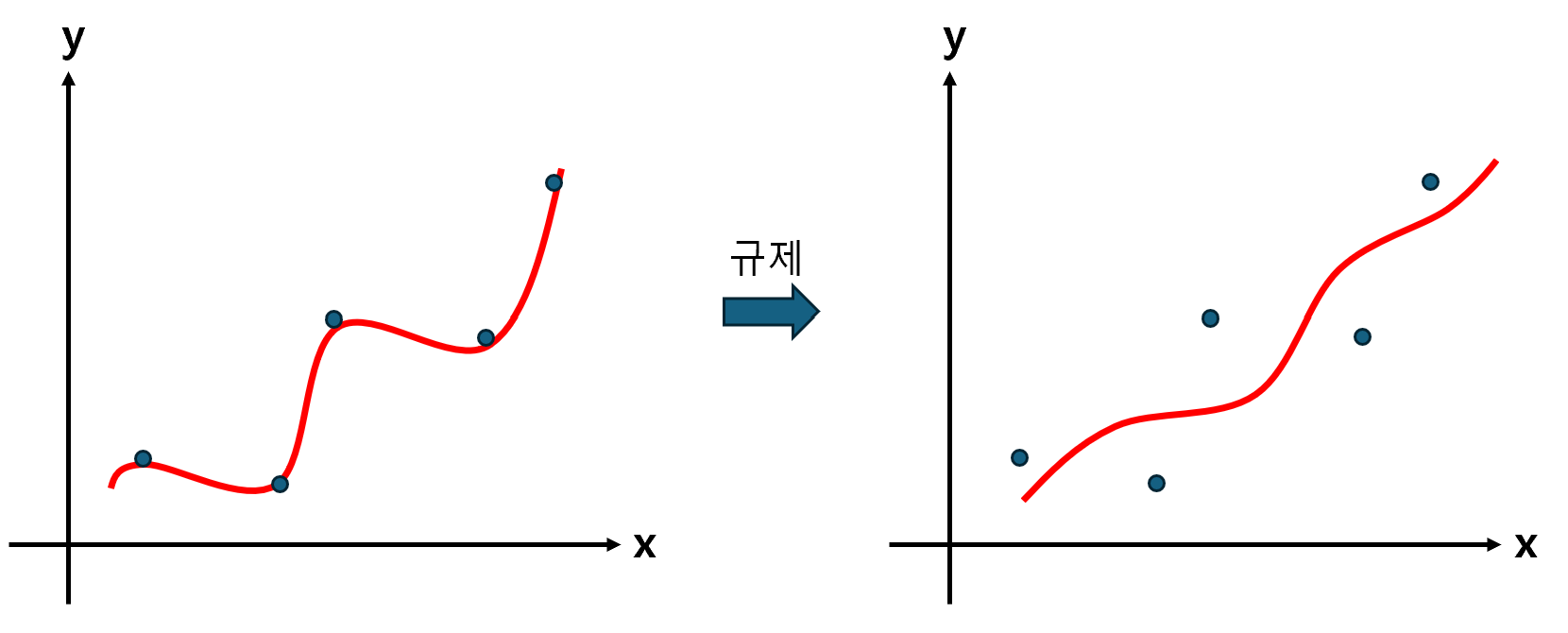
그래프가 오른쪽 그림처럼 변경되면, 분명 훈련 Set에서의 성능은 낮아질 것이다. 하지만, 훈련 Set의 전반적인 패턴만 학습하게 되면서, 일반화 성능은 크게 향상된다. 즉, 방정식의 계수(기울기)를 조절하는 것으로, 과대 적합 문제를 효과적으로 해결할 수 있다는 것이다.
2) 변량 정규화하기
각 변량의 계수를 공평하게 조절하기 위해서는, 각 변량을 정규화(데이터 전처리)할 필요가 있다. 지난 포스팅에서는 데이터 전처리를 위해 평균과 표준편차를 직접 구해, Standard Score을 계산하였다. 그러나 사이킷런의 StandardScaler라는 Transformer 클래스를 사용할 경우, 직접 평균과 표준편차를 구하지 않고도 Standard Score로 정규화가 가능하다.
참고로, Estimator 클래스가 fit(), score(), predict() 메서드를 공유하듯, Transformer 클래스도 fit(), transformer() 클래스를 공유한다.
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_poly)
train_scaled = ss.transform(train_poly)
test_scaled = ss.transform(test_poly)이렇게 해서 정규화된 훈련 Set과 테스트 Set이 모두 준비되었다.
3) 규제가 적용된 선형 회귀 모델의 종류
선형 회귀 모델에 규제를 추가한 모델은, Ridge와 Lasso로 구분된다.
① Ridge 모델
- 계수의 제곱 값을 기준으로 규제를 적용한다.
- 일반적으로 선호되는 모델이다.
② Lasso 모델
- 계수의 절대값을 기준으로 규제를 적용한다.
- 무의미한 특성의 계수를 0으로 만들 수 있다.
5. Ridge 회귀와 Lasso 회귀
1) Ridge 회귀
먼저 Ridge 모델부터 훈련시켜보도록 하겠다.
from sklearn.linear_model import Ridge
ridge = Ridge()
ridge.fit(train_scaled, train_target)이제 훈련 Set과 테스트 Set에서 모델의 성능을 평가해보자.
print(ridge.score(train_scaled, train_target))
print(ridge.score(test_scaled, test_target))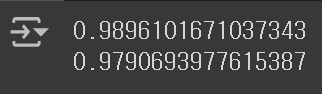
비록, 훈련 Set에서의 점수는 조금 낮아졌지만, 테스트 Set에서의 점수가 회복되었다는 점에서 의미가 있다. 이렇듯 규제를 적절히 활용하면, 다양한 특성을 유지하면서도 훈련 Set에 과대 적합되는 문제를 예방할 수 있다.
물론, 규제의 정도를 직접 조절하는 것도 가능하다. 조절에 사용되는 매개변수는 alpha이며, alpha의 크기는 규제의 강도와 비례한다. 즉, alpha 값을 증가시키면 과소 적합을, alpha 값을 감소시키면 과대 적합을 유도하게 되는 것이다. 참고로, alpha는 하이퍼 파라미터이므로, 적절한 값을 직접 찾아주어야 한다.
※ Hyperparameter
하이퍼 파라미터란 머신 러닝 모델이 알아서 학습할 수 없는 값으로, 사람이 직접 지정해주어야 하는 매개변수를 의미한다.
적절한 alpha 값을 찾는 대표적인 방법은 각 alpha 값에 대응되는 R² 값을 Scatter Flot으로 그려보는 것이다.
import matplotlib.pyplot as plt
train_score = []
test_score = []
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
for alpha in alpha_list:
ridge = Ridge(alpha=alpha)
ridge.fit(train_scaled, train_target)
train_score.append(ridge.score(train_scaled, train_target))
test_score.append(ridge.score(test_scaled, test_target))그런데, alpha 값이 10배씩 증가하기 때문에 alpha 값을 그대로 x 좌표에 사용하면, 그래프의 왼쪽은 간격이 너무 좁고, 오른쪽은 간격이 너무 넓은 그래프가 그려질 것이다. 따라서, 6개의 alpha 값이 모두 동일한 간격을 가질 수 있도록, alpha의 값을 Log Scale로 변환해 표시하기로 하겠다. 참고로, Numpy에서 제공하는 로그 변환 메서드는 자연로그로 변환하는 np.log()와 상용 로그로 변환하는 np.log10()이 있다.
plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)
plt.xlabel('alpha')
plt.ylabel('score')
plt.show()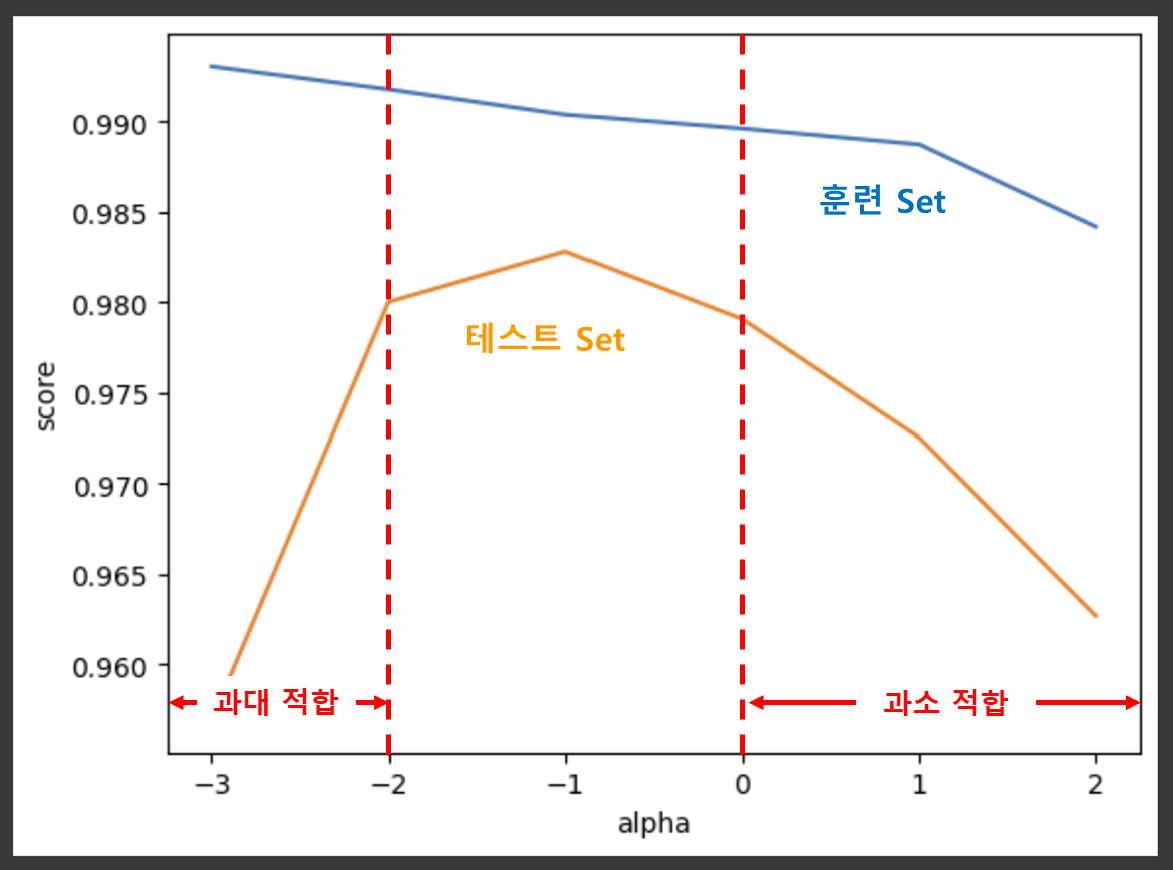
그래프의 왼쪽 부분에는, 훈련 Set에 특화되어 일반화 성능이 떨어지는 과대 적합의 전형적인 양상이 나타났다. 반대로, 그래프의 오른쪽 부분에서는 훈련 Set에서의 성능과 테스트 Set에서의 성능이 모두 낮은 과소 적합의 양상이 나타나고 있다. 따라서, 가장 적절한 alpha 값은 두 그래프의 점수 차이가 가장 작으면서(가장 가까우면서) 테스트 Set의 점수가 가장 높은 0.1이 될 것이다.
ridge = Ridge(alpha=0.1)
ridge.fit(train_scaled, train_target)
print(ridge.score(train_scaled, train_target))
print(ridge.score(test_scaled, test_target))
적절한 alpha 값을 사용함으로써, 훈련 Set과 테스트 Set에서 모두 좋은 성능을 보이는 Ridge 모델이 완성되었다.
2) Lasso 회귀
이번에는 Lasso 모델을 훈련시켜보기로 하자.
from sklearn.linear_model import Lasso
lasso = Lasso()
lasso.fit(train_scaled, train_target)이제 훈련 Set과 테스트 Set에서 모델의 성능을 평가해보자.
print(lasso.score(train_scaled, train_target))
print(lasso.score(test_scaled, test_target))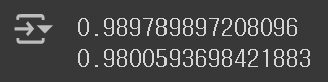
Lasso 모델에서도 과대 적합이 잘 억제되었음을 확인할 수 있다. 그렇다면 Lasso 모델에서의 최적의 alpha 값은 얼마일까? 이번에도 마찬가지로 Scatter Flot을 통해 최적의 alpha 값을 찾아보자.
import matplotlib.pyplot as plt
train_score = []
test_score = []
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
for alpha in alpha_list:
lasso = Lasso(alpha=alpha, max_iter=10000)
lasso.fit(train_scaled, train_target)
train_score.append(lasso.score(train_scaled, train_target))
test_score.append(lasso.score(test_scaled, test_target))
plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)
plt.xlabel('alpha')
plt.ylabel('score')
plt.show()아래와 같은 Warning이 발생할텐데, 이는 max_iter 매개 변수와 관련이 깊다. Lasso 회귀에는 최적 값을 알아내기 위한 반복적인 알고리즘이 사용되므로, max_iter 매개 변수를 통해 최대 반복 횟수를 제한할 수 있다. 만약, 최대 반복 횟수만큼 반복했음에도 최적 값이 수렴하지 않으면, 값이 수렴하지 않았다는 경고 표시가 나타나는데, 아래의 Warning이 바로 그것이다.
/usr/local/lib/python3.10/dist-packages/sklearn/linear_model/_coordinate_descent.py:631: ConvergenceWarning: Objective did not converge. You might want to increase the number of iterations, check the scale of the features or consider increasing regularisation. Duality gap: 1.878e+04, tolerance: 5.183e+02
model = cd_fast.enet_coordinate_descent(
/usr/local/lib/python3.10/dist-packages/sklearn/linear_model/_coordinate_descent.py:631: ConvergenceWarning: Objective did not converge. You might want to increase the number of iterations, check the scale of the features or consider increasing regularisation. Duality gap: 1.297e+04, tolerance: 5.183e+02
model = cd_fast.enet_coordinate_descent(이러한 Warning이 발생할 경우, max_iter 값을 늘려야 하지만, 이번 실습에서는 별로 중요한 내용이 아니므로, 무시하고 넘어가기로 한다.
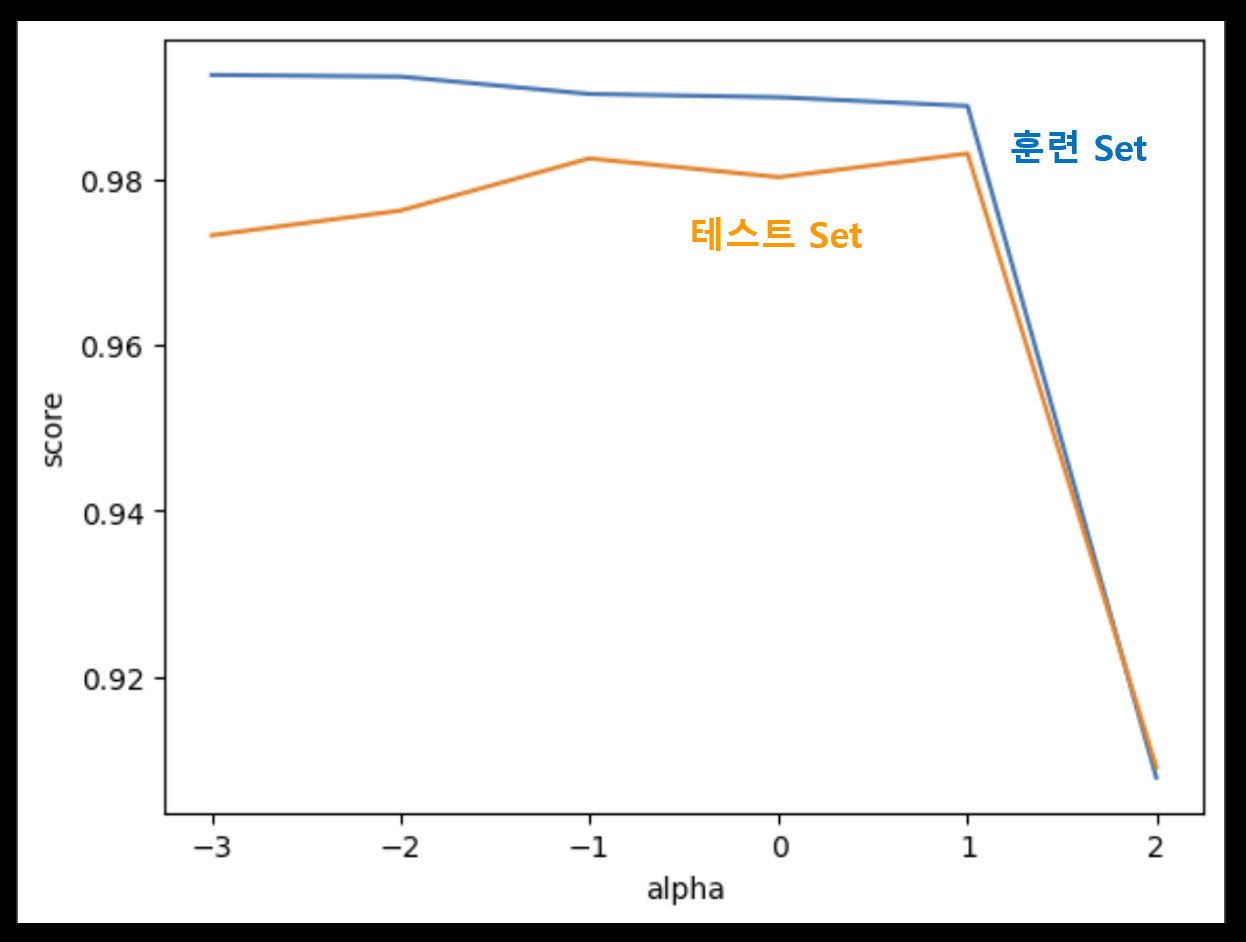
이번에도 왼쪽 부분에서는 과대 적합, 오른쪽 부분에서는 과소 적합의 양상이 나타난다. 위 Scatter Flot에서 두 그래프가 가장 가까워지면서, 테스트 Set의 점수가 가장 높아지는 지점이 alpha가 10일 때이므로, 최적의 alpha 값을 10으로 결정할 수 있다.
lasso = Lasso(alpha=10)
lasso.fit(train_scaled, train_target)
print(lasso.score(train_scaled, train_target))
print(lasso.score(test_scaled, test_target))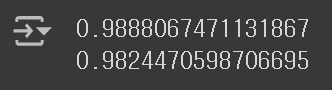
이번에도 훈련 Set과 테스트 Set에서 모두 좋은 성능을 보이는 Lasso 모델을 만드는 데에 성공하였다.
추가적으로 Lasso 모델이 얼마나 많은 계수를 0으로 설정했는지 확인해보자. Lasso 모델의 계수는 coef_ 속성을 통해 확인할 수 있다.
print(np.sum(lasso.coef_ == 0)) # 40 출력55개의 특성 중 무려 40개의 특성을 사용하지 않았다. 사실, 우리가 주입한 55개의 특성 중 대부분이 무의미한 데이터이다보니, 어찌 보면 당연한 결과이다. 이렇듯 Lasso 모델은 계수를 0으로 만들 수 있다는 특징 덕분에 유의미한 특성만 골라내야 할 때, 유용한 모델이다.
