SGDClassifier

확률적 경사 하강법(Stochastic Gradient Decent:SGD)을 통해 SVM, logistic regression 등의 선형 분류기를 학습시킬 수 있는 분류기입니다. (sklearn API 설명)

SGD?

Stochastic Gredient Decent: 확률적 경사 하강법의 약자로, 손실 함수의 기울기가 최소가 되게 하는 지점을 찾아내는 경사하강법의 한 방법이다.

경사하강법??

비용 함수 $f$의 함숫값이 줄어드는 방향으로 함수의 계수를 일정 크기(학습량)만큼 더해나가며 $f$의 최솟값을 찾는 최적화 기법이다.

기울기: Gradient의 정의

• $Gradient(f) = ∇f(x)=[\frac{∂f(x_0)}{∂x_0},\frac{∂f(x_1)}{∂x_1},..., \frac{∂f(x_{N-1})}{∂x_{N-1}}]^T$
• 미분 가능한 $N$개의 다변수 함수 $f$를 각 축에 대하여 편미분한 값으로, 스칼라 함수의 모든 축에 대응하는 벡터장을 생성하는 역할을 한다.

경사하강법의 예

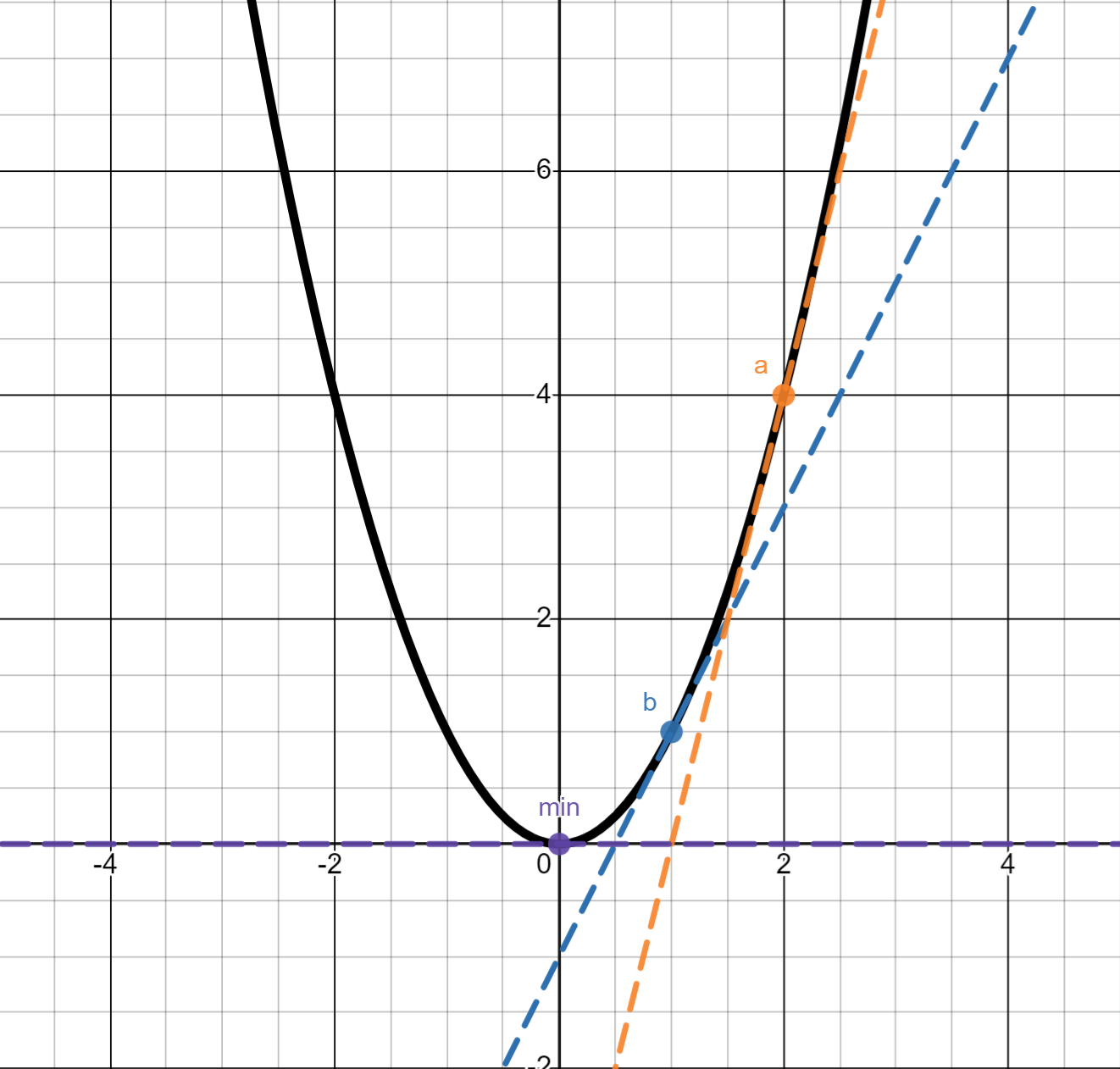
함수가 $y=x^2$이고 학습률 $w$가 $1$일 때 경사하강법을 통해 최솟값 $min$에 도달하는 과정을 보자. 최초에 점 $a$에서 시작하여 점 $b$를 지나 점 $min$으로 수렴하는 모습을 볼 수 있다. 이 때 각 step마다 $Gradient$는 계속해서 줄어드는 것 또한 관찰할 수 있다.

경사하강법의 한계

• 손실 함수가 조금만 복잡해져도 Global Minimum을 발견하지 못한 채 Local Minimum에 빠지기 쉽다.
• 학습 시간이 길다.

확률적 경사하강법(SGD)

각 학습마다 모든 배치가 아닌 일부 샘플을 랜덤으로 선택하여 학습에 이용한다는 것이 '확률적'의 의미이다.

• 학습 속도가 경사하강법에 비해 빠르지만 랜덤하게 선택된 데이터에 의해 노이즈가 발생할 수 있다.

보통 일반적으로 말하는 SGD는 엄밀하게는 미니 배치 확률적 경사하강법을 의미한다.

• 각 학습마다 모든 배치를 학습 대상으로 사용하지 않고 랜덤으로 선택된 n개의 배치를 학습에 이용하여 그 평균 경사를 구한다.
• 경사하강법과 확률적 경사하강법을 절충한 방법이다.

SGDClassifier

확률적 경사하강법을 이용하는 선형 이진 분류기이다.

• loss=hinge, penalty='l2인 경우 규제가 있는 선형 SVM 분류기를 SGD 방식으로 학습시킨다.
• loss=log_loss인 경우 로지스틱 회귀 분류기가 선택된다.
• alpha는 규제의 강도를 설정한다.
• tol은 정밀도이며 None이 아닌 경우 $loss > best\_loss - tol$일 때 학습을 종료한다.
• eta0은 초기 학습률이다.
• learning_rate는 학습 속도이다.

규제?

선형 모델의 경우 모델이 훈련 데이터에 과적합되는 문제가 자주 발생한다. 이는 비용 함수의 최소화, 즉 실제와 예측과의 차이만을 최소화하는 방법으로 돌아가다 보니 필연적으로 과적합 문제가 생길 수 밖에 없다.

Ridge

• 모델의 손실 함수 최소화라는 목표에 추가로 가중치에 대한 목표를 만든다.
• 가중치의 절댓값을 최대한 작게 만드는 것을 목표로 한다. 이는 결국 기울기를 작게 만드는 것이다.
  - 각 가중치 제곱합에 규제 강도 α를 곱하여 오차에 더하는 것으로, l2 규제라고도 한다.

Lasso

• Ridge 규제와 같이 가중치를 최소화하는 것을 목표로 한다.
• 가중치의 제곱합이 아닌 가중치의 합에 α를 곱하여 오차에 더하는 것으로 l1 규제라고도 한다.
  - l2 규제와는 다르게 어떤 가중치 $w$가 0이 될 수 있다. 즉 모델에서 완전히 제외되는 특성이 생길 수 있다.

ElasticNet

• Lasso와 Ridge를 결합한 것으로, l1과 l2 규제의 비율을 설정해주어야 한다.