Game Engineering 6

LeemHyungJun·2023년 5월 9일

Game Engineering

목록 보기

4/8

Heuristic Inverse Kinemtics Algorithms

Introduction

Heuristic
- 대충, 잘...
- 반복적이고 계산이 많이 드는 작업을 좀 더 빠르게 하는 방식

1. Cyclic Coordinate Descent

Heuristic의 시초
CCD
position과 orientation의 error를 최소화 하는 기법
end effector에서 시작해서 닿으려고 하는 target으로 계속 회전시키는 기법 (만족하는 해가 나올때 까지 반복)

2. Triangulation IK

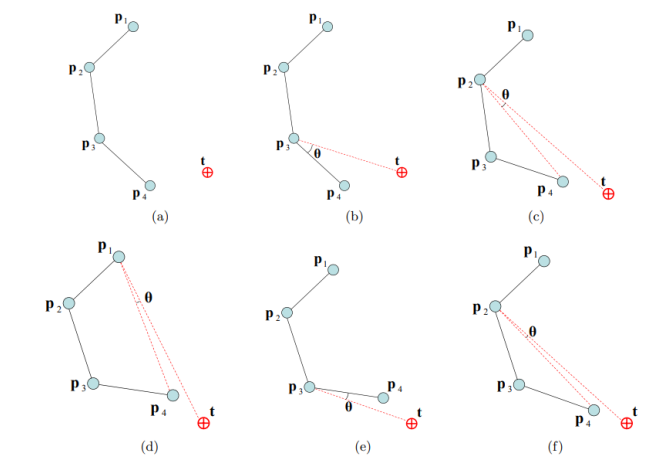
Law of Cosines for IK
joint에 제한 조건이 없고, target이 range 안에 있는 경우 무조건 해를 찾을 수 있는 방법이다.
장점:
- computational power가 CCD에 비해 낮다.
- 1번의 iteration만 돌면 해를 구할 수 있다.
단점:
- end effector가 여러 개인 경우 해를 풀기 어렵다.
- 제한조건이 생기면 문제를 풀 수 없어진다.
- 문제를 풀었을 때 해의 결과가 부자연스러운 모습이 발생한다.

3. Sequential Inverse Kinematics (SIK)

sequential Analytic-iterative IK
- 3d human full-body movement 를 reconstruct 할때 사용 (VR, 모션 캡쳐)
- input값
  - end effector positions (wrists, ankles, head..)
- procedures
  1) input으로 들어온 position에서 root joint를 설정 (대체로 wrist, heap)
  2) root와 head를 연결하여, spine을 구성
  3) spine의 position과 end effector의 위치를 통해 clavicles의 방향 결정
  4) 팔, 다리 등의 사지의 위치를 end effector의 위치를 통해 대충 그리기

4. FABRIK

4-1. FABRIK Intro

A fast, iterative solver for the Inverse Kinematics Problem
- 지금까지 만들어진 IK 방식 중에서 가장 좋고, 가장 빠른 방식
FABRIK (Forward and Backward Reaching Inverse Kinematics)
- 간단하게 말하면 end effector에서 앞으로 나아가며 계산하고, 끝까지 도달하면, 다시 end effector로 향하는 방향으로 계산하는 방식이다.
- 장점 :
  - low computational power
  - fewer iterations
  - visually realistic
- procedures
  - 모든 joint 사이의 길이( $d$ )를 계산한다.
  - 계산한 길이를 모두 더한 값을 통해 target에 닿을 수 있는지 없는지 확인한다.
  - 만약 닿을 수 있다면, 쭉 펴진 형태로 결과가 나오고, 닿을 수 없다면, 위에서 언급한 방식으로 2-stage iteration을 실행한다.
  - 1st stage
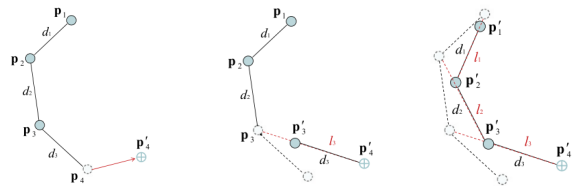
    - target $t$ 로 $p_n'$ 을 이동 이후에 $l_{n-1}$ 을 계산하여 차례대로 $p$ 와 $l$ 을 계산하여 기존의 $d$ 와 비교하며 이동시킨다.
    - 결과적으로 root $p$ 가 기존의 위치에서 떨어지게 되는데, 이렇게 되면 부자연스러운 결과가 나온다.
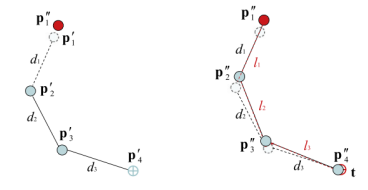
  - 2nd stage
    - 1st stage했던 방식과 마찬가지로 반대로 올라가면서 실행하여 root $p$ 를 기존의 위치로 돌려준다.

4-2. Overcome the limits of other method

FABRIK with Multiple End Effector
- 위에서 언급한 방식들의 한계점인 end effector가 여러개인 상황을 개선하는 방식
- sub-base를 이용한다!
  - 예를들어 pelvis 라는 sub-base joint를 선택하여, left leg와 right leg를 연결한다.
  - left leg와 right leg를 각각 계산한 후, 각각의 root를 평균을 계산하여 pelvis(new sub-base)를 계산한다.
  - 이후로 다시 sub-base에서 root로 FABRIK을 계산한다.
  - 이 방식에 있어서도 1st와 2nd stage를 반복한다.
FABRIK with Joint limits(constraints)
- Intro
  - 게임에서 IK를 사용한 human model은 자연스러움을 위해 constraints가 필수적이다.
  - re-positioning과 re-orientation 방식을 이용한다.
  - 3d->2d 방식을 이용하기 때문에 복잡도가 낮다.
- Idea
  - dof를 분석하여 $\theta$ 값을 이용하여 cone 모양으로 나타낸다.
  - $\theta$ 가 모두 동일한 경우 cone 모양
  - $\theta$ 가 동일하지 않다면, 비스듬한 cone 모양이 된다.
    - 이때 평면으로 cone을 자르게 되면 ellipse 혹은 parabolic이 된다.
- Setting
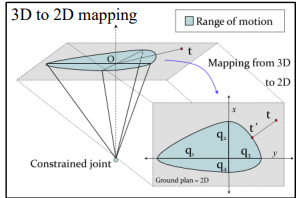
  - $\theta_1, \theta_2, \theta_3, \theta_4$ 를 계산하여, cone을 구성하고 계산을 편하게 만들기 위해서 2d 평면 상으로 projection을 한다.
  - target $t$ 를 계산하기 위해서 $t'$ 을 이용하게 된다. 이때 $q_2,q_3$ 만 이용해서 계산이 가능하다.
- procedures example
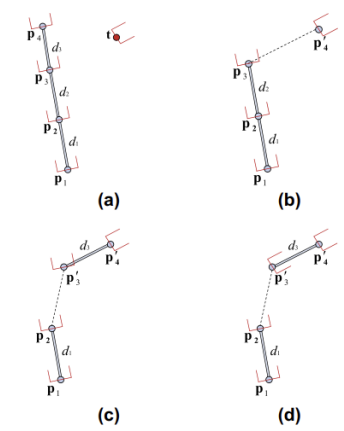
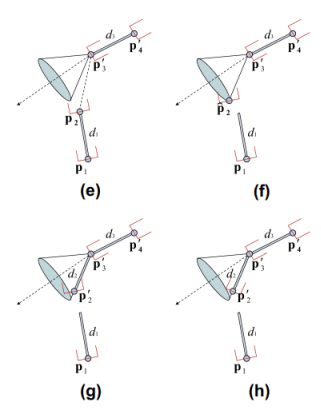
  - relocate and reorient point $p_{4}$ to $t$
  - $p_3$ 를 이동 시킨 후, $p_4$ 와 orientation을 맞춰주기
  - $p_2$ 를 이동 후, $p_3$ 의 제약 조건에 맞춰주기 위해서 relocate
  - 이후 $d_2$ 길이를 보존시키기 위해서 relocate
  - 마지막으로 $p_2$ reorientation
  - 결과값을 구할때 까지 반복
- procedures picture