Quasi-Newton Method for IK
Introduction
- Newton Method 에서 2차 미분 형태
- 장점 : converge more quickly
- 단점 : 계산이 많다. -> Quasi-Newton method로 hessian을 근사하기!
- Quasi-Newton's flow
- optimal solution을 위한 초기값 설정
- gradient (1차미분) 계산
- Hessian (2차미분) 근사
- 근사한 Hessian으로 solution update
- iteration (위의 step 반복)
- Quasi-Newton
- 장점
- computational 복잡도 감소
- 빠른 convergence (for ill-condition)
- initial guess에 less sensitive함
- 단점
- hessian 정확도 감소
- 특정 문제에서 느린 convergence (IK의 경우 아크로바틱한 문제에서 어려움을 겪음)
- 장점
Basics
1. Ill-conditioned problem
- hessian의 condition number가 너무 커서 optimization이 어려운 상황
- condition number of matrix : 가장 큰 eigen value와 가장 작은 eigen value간의 비율
-> eigen value 간의 차이가 너무 클때
-> 수렴치가 한 축으로만 쏠리는 현상 발생 (numerical unstable)
- condition number of matrix : 가장 큰 eigen value와 가장 작은 eigen value간의 비율
- Ill-condition의 원인
- poor scaling of varialbles
- high-dimensional problem (파라메터가 너무 많을 때)
- objective function 자체의 문제
- 해결 방안
- appropriate variable scaling
- preconditioning
- use optimization algorithm
2. Definite Matrix
- 의미
- Positive, negative, indefinite 한 지 미리 구별하는 방법
- objective function의 curvature를 알 수 있다.
-> convergence and stability 파악 가능
- 구하는 방법
의 transpose : , n-dimensional zero-vector : 0
n x n symmetic real matrix M에 대하여
Positive-definite :
Positive-semidefinite, non-negative-definite :
negative-definite :
negative-semidefinite, non-positive-definite : - 개념
- Hessian Matrix of function 이 점 p에서 positive definite한 경우 그 function은 p근처에서 convex 하다
-> iterative 하면 해를 찾을 수 있다는 의미!
- Hessian Matrix of function 이 점 p에서 positive definite한 경우 그 function은 p근처에서 convex 하다
- 특징
- positive-definite matrix
1) all positive eigen value
2) invertible
3) symmmetric
4) convex / unique global minimum -> converge to unique point - negative-definite matrix
1) all negative eigen value
2) invertible
3) symmetric
4) concave / unique global maximum -> converge to unique point - indefinite matrix
1) negative and positive eigen value
2) symmetric (real matrix)
- positive-definite matrix
3. Secant Method
- 개념
- 1차 미분을 구하기 어려울 때, 1차 미분의 유사값을 찾는 방법
- root finding algorithm (Newton-method 랑 유사한 방식)
- 이전의 두 점을 가지고 미분 값을 찾는 방법
에서 가 secant method의 의미
4. Frobenius norm (Euclidean norm)
- 개념
- matrix의 size를 구하기 위한 matrix norm
- 정의
- 특징
- trace property와 관련이 있다.
- trace property : matrix의 diagonal을 더한 값
- trace of square matrix A :
- conjugate transpose of A :
squared Frobenius norm을 다시 정의하면
(real matrix에서는 )
- trace property와 관련이 있다.
5. Lagrane Multiplier
- 개념
- 제한이 걸려있는 상황에서 최적화 문제를 푸는 방법
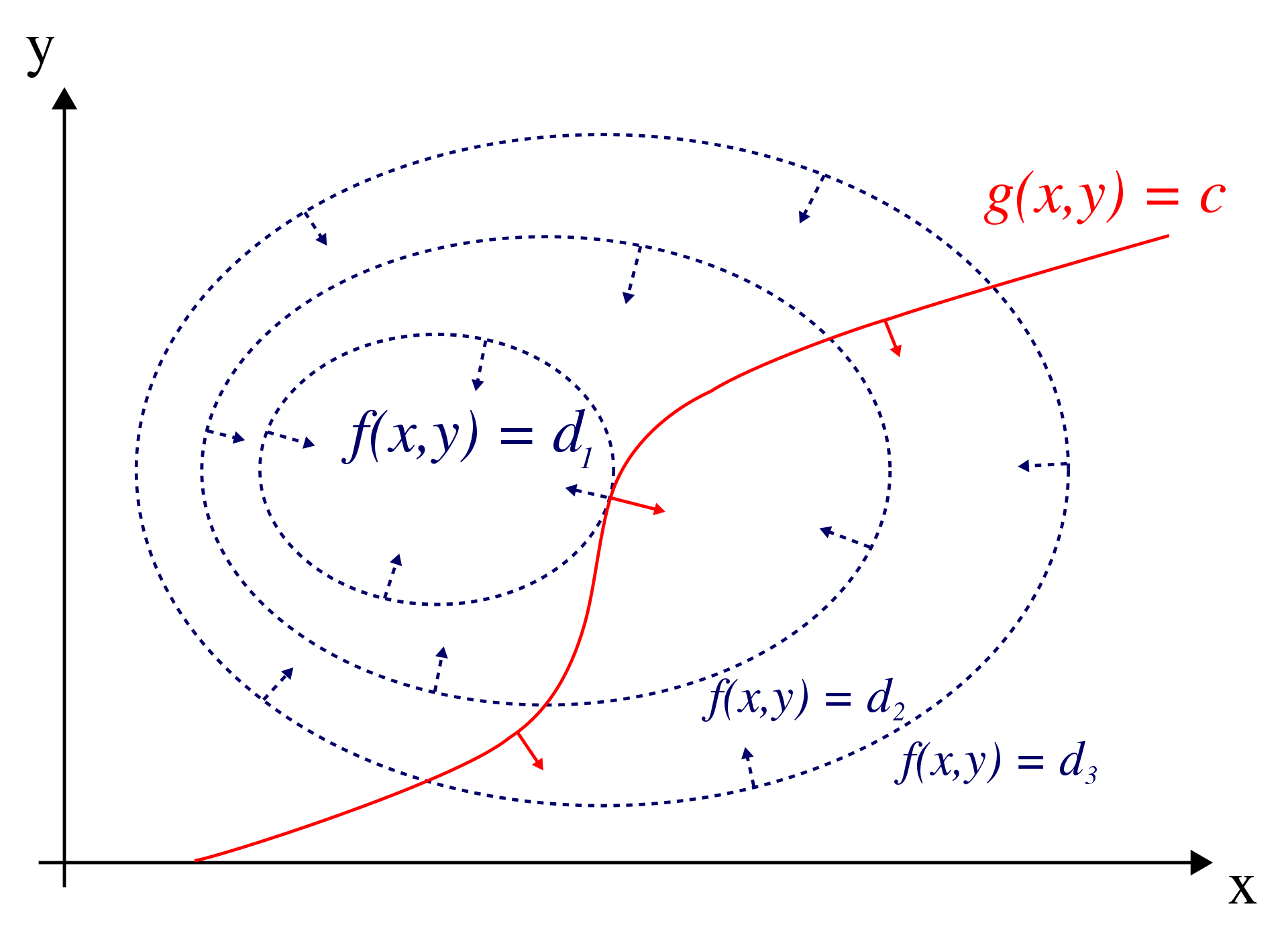
- 그림에서
- 가 objective function
- 가 constraint
- 이 제한 상황에서 maximum 구한 것
- 수식
- Lagrange function :
-> 가 Larange multiplier- 위의 식을 편미분 하고 각 식들이 0이 되는 값을 연립해서 풀기
Quasi-Newton Method
-
목표
- scalar-valued function의 minimum or maximum 을 구하기
- = search for zero of the gradient of that function
-
수식
(
Newton method에서의 문제 :
-> Hessian을 쉽게 푸는 것이 목적! -
과정 (Hessian 간단하게 하기)
- secant equation (Taylor series)
-> 미분
->
-> 과 에서 Hessian의 값 차이가 없다면..
(는 Hessain 근사)
- secant equation (Taylor series)
-
Quasi-Newton steps
1) 풀기
2) learning rate 결정
3) update -
Quasi-Newton 방식들
- 지금까지의 방식들 중 가장 좋은 방식은 BFGS
- Broyden, DFP, SR1 등이 있음
Broyden-Fletcher-Goldfarb-Shanno Method
Broyden Method
- 목적: 과 간의 Frobenius norm을 최소화 하기
-> - subject to (조건)
->
-> - 위의 문제는 제한 조건이 있는 문제이므로
-> 풀면 - 정리
식과
식을 연립
Frobenius (trace property) 에 의하여
-> 결론 :

Immerse yourself in the vibrant mosaic of fun and fellowship, where every click of your mouse heralds a new chapter in the saga of endless excitement. Explore the dynamic space where the thrill of play intertwines seamlessly with the ㅤ joy of forging meaningful connections, and let the digital landscapes resonate with the eternal symphony of excitement that defines this vibrant community