
Computer Animation Algorithms & Techniques (By Rick Parent)
책을 정리한 내용입니다. (틀린 내용이 있을 수 있습니다)
Fluids: Liquids & Gases
- 컴퓨터를 통해 모델링하고 애니메이션하기에 가장 어려운 객체가 정적이고, 고정적이며, 단순한 구조로 정의되지 않은 객체들이다.
ex) 불, 구름, 물- 유체에 대한 컴퓨터 처리를 Computational Fluids Dynamics 라고 한다.
8.1 Specific Fluids Models
8.1.1 Models of Waters
- 물은 bump mapping과 같이 곡면의 법선벡터를 수정하여 잔물결을 표현한다.
- 물은 시간에 따라 곡면의 기하도형과 결합하는 형태를 가진 채로 굴러가는 height-field 형태로 모델링 될 수 있다.
- Still Waters and Small-Amplitude Waves
-> Normal vector perturbation을 이용하면 작은 진폭파의 모양을 시뮬레이션 하는데 사용할 수 있다. - The Anatomy of Waves
- Modeling Ocean Waves
- Finding Its Way Downhill
8.1.2 Modeling and animating clouds
- Anatomy of clouds and cloud formation
- Cloud models in CG
8.1.3 Modeling and animating fire
- Procedurally Generated Image
-> 불을 표현하는 가장 쉬운 방법은 화염과 연기를 연상하게 하는 pixel로 절차적 2차원 영상을 생성하는 것이다.
-> 다중 버퍼와 alpha 채널을 사용하여 제한된 3차원 효과를 낼 수 있다. - Particle System approach
- 폭발류 파티클의 2단계 구조(레벨)
1) 초기 폭발을 시뮬레이션하기 위한 충돌 지점
2) 파티클들이 동심의 고리로 구성되며, 중심에서 바깥쪽으로 진행되는 것에 맞추어 불의 폭발이 형성
-> 두번째 레벨의 고리들은 개별적인 파티클 시스템으로 구성되고, 중첩되어 나타난다. (Figure 8.15)
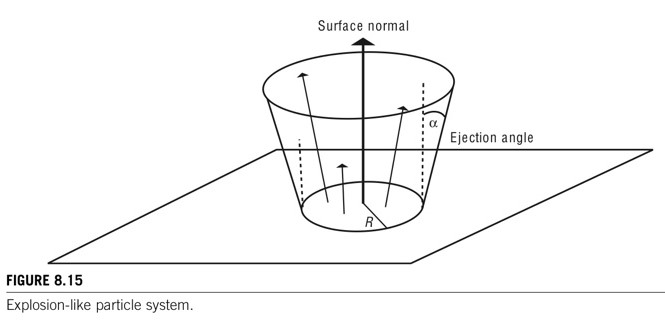
- 폭발류 파티클의 2단계 구조(레벨)
- Other Approaches
1) 2차원 텍스쳐맵 : 시점이 특정 방향일 때만 유효함
2) two-dimensional-multiple planes : 불에 대한 깊이를 추가(방향은 제한적)
3) advection-diffusion : 바람에 대한 field를 만들어 적용(수학적으로 복잡함)
8.2 Computational Fluid Dynamics
- 기체와 액체(Fluid)의 동작을 계산하는 컴퓨터 기술을 CFD라고 한다.
- CFD에서는 유체는 특성(밀도,온도,운동량)들이 무한히 작은 지점에서 정의되고, 부드럽게 변화하는 연속적인 매체라고 가정한다.
- 유체는 기하학적 구조를 가지고 있지 않고, 위상학적 구조를 가지지 않는다.
-> 기체는 compressible / 기체의 밀도가 공간상에서 가변적이고, 밀도의 변화를 계산하는 것에 비용이 든다.
-> 액체는 incompressible / 액체의 밀도는 상수이다.
8.2.1 General Approaches to Modeling Fluids
- Grid-Based Method
- 공간을 cell로 분할하고, 각 cell에서 기체의 흐름을 계산한다.
- cell 내부 기체의 밀도는 단위시간마다 갱신되고, 랜더링 과정에서 visibility와 illumination을 결정한다. (속도, 가속도, 밀도 등 이용)
- 단점 : 공간을 cell로 분할시 정적인(동적 데이터는 계산량 증가) 데이터 구조를 이용한다면, 시뮬레이션을 하기 위한 공간의 범위를 확장하는 작업이 필요하다.
- Particle-Based Method
- 파티클은 개별적으로 만들거나, 주어진 밀도의 기체 범위로도 만들 수 있다.
- 장점 : 강체역학과 비슷하여 수식이 간단하다.(회전 역학만 무시하면 단순화 가능) 기체가 이동하기 위한 시뮬레이션 장치에는 제한을 주지 않는다.
- 단점 : 기체의 밀도와 팽창력을 시뮬레이션하기 위해서는 많은 양의 파티클이 필요하다
- Hybrid Method
- grid 내에 있는 파티클을 추적하는 모델(파티클은 cell과 cell 사이를 지나감)
- 파티클은 디스플레이를 만들기 위해 grid 속에서 속성을 전달하고 분배
- grid는 디스플레이를 만드는데 사용
8.2.2 CFD Equations
-
volume은 작은 fluid 요소들로 분석되고, 해당 요소들에 대한 미분 방정식이 만들어진다.
-
전체 CFD 방정식은 닫힌 시스템에서 아래의 식으로 구성된다.
1) 질량 보존
2) 운동량 보존
3) 에너지 보존 -
방정식으로 표현할 때 Navier-Stokes 방정식이라고 한다.
-> NS 방정식은 선형미분 방정식이며, 그래픽스 분야에서 간소화하는 방법이 있다.
1) 에너지 보존 무시
2) 유체는 비점성
3) 유체는 밀도가 변하지 않음(액체일때)
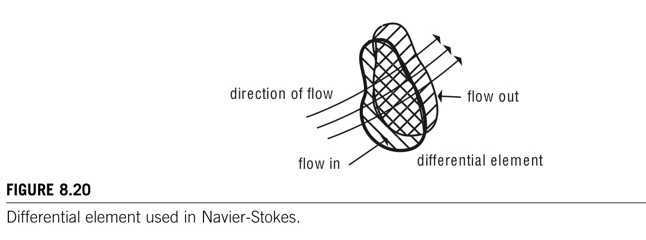
-
Conservation of Mass
- 질량 보존은 연속 방정식에 의해 표현된다.
- : 밀도 : 압력 : x방향에 수직인 면의 흐름 : cell의 부피
->
-> cell 차원에서 부피V와 영역A를 치환
-> 로 나눔
-> 치환과 방향의 유동을 포함
(식 1)
->
-> (식 1에 발산 연산자 이용)
=> 유체가 압축될 수 없으면, 밀도도 변하지 않는다.
이므로
-
Conservation of Momentum
- 유체의 운동량 = 밀도 x 유체의 부피 x 유체의 평균 속도
- 3차원 cell에서 x방향만 생각
->
-> 위 식을 치환
-> 방향 모두 고려하고, x방향의 운동량을 분류하면 아래와 같다.
-
방정식 풀이
-> cell에서의 경계조건이 필요하다.
-> 격자의 각 cell에서 CFD 방정식은 행렬 방정식의 희소 집합 생성
-> LU와 결합증감 등으로 희소 행렬을 해결한다. -
안정된 유동체
-> Navier-Stokes 방정식은 공학적으로 정확하지 않지만, 그래픽스에서 사용하기에 유용하다. -
밀도 갱신
밀도 방정식 ( : 밀도, : 밀도를 변화시키는 다른 요인, : 밀도의 발산, : 속도 영역에 따른 이류)-> 첫항 : 사용자 상호작용이나 환경에 의해 지정된 밀도 소스 배열
-> 둘째항 : 각 셀로부터 이웃 셀까지 밀도 확산
-> 셋째항 : 속도 영역에 따라 밀도를 이류 -
속도 갱신
속도 방정식( : 외부힘)-> 첫항 : 사용자나 환경으로부터 더해짐
-> 둘째항 : 속도의 확산 허용
-> 셋째항 : 속도 영역에 의해 수행되도록 속도 허용
