Computer Animation Ch.7

Computer Animation Algorithms & Techniques (By Rick Parent)
책을 정리한 내용입니다. (틀린 내용이 있을 수 있습니다)

Physically Based Animation

• 물리학에 기반한 애니메이션의 경우 각 위치와 중심점(orientation)을 정확히 제어하는 것보다 보편적인 움직임에 관심이 많다.
  -> 물리적 정확성(실제 현상에서 발생하는 일)이 중요한 것이 아니라 애니메이터가 원하는 모션에 제한사항을 중요시한다.
• 일반적인 유형을 특성화 (프로그래머가 원하는 모습을 만들기)
  -> 적은 계산, 프로그래밍하기 쉬움 / 유연성 부족
• 실제 물리적인 현상을 적용
  -> 많은 계산, 유연함, 더 큰 범위의 특성 표현 가능
• 물리적 모델을 사용할때의 장점 : motion의 low-level specification을 줄이고 motion의 high-level한 관계나 특성을 지정하는 것만 필요하다는 점이다.

7.1 Basic Physics - A Review

• $f = ma$
• $v' = v + a\Delta t$
• $p' = p + \frac{1}{2}(v + v')\Delta t$
• $f=\frac{Gm1,m2}{d^2}$
• 스프링 정지 길이($L_r$), 스프링 현재 길이($L_c$), 비례상수($k_s$)
  -> Spring : $f_d = k_s(L_c-L-_r)$
• 감쇠력 ($f_d$), 스프링 길이의 속도 ($v_s$)
  -> Damper : $f_d = -k_dv_s$
• 점성의 힘($f_v$), 속도($v$)
  -> viscosity : $f_v = -k_vv$
• 운동량
  -> $\sum m_iv_i = c$
• 토크
  -> $\tau = I\omega$

7.1.1 Sumulating a Spring-mass-damper System

• $f=k_s(L_c-L_r)+k_dv_s$

7.2 Spring Meshes

7.2.1 Flexible Objects

• Flexibility는 mass-spring-damper 시스템에 의해 모델링 된다.
• Spring-Mass-Damper Modeling of Flexible Objects
  -> 객체의 모든 점을 point mass로 객체의 개별 선분을 spring으로 보는 것
  -> 한 정점에 가해진 힘은 스프링 힘을 유도하고 인접한 정점에 힘을 가하게 되어 움직임이 반복된다.
  -> 단점: 객체를 모델링 하기 위해서는 vertex가 필요하고, 힘에 대한 객체의 반응을 모델링하기 위해서는 edge가 필요하다.
  -> spring-mass modeling의 경우 값의 인위적인 수정이 필요(값이 발산 하기 때문)하기에 시뮬레이션의 결과가 원하지 않는 결과가 나오게 된다.
  해결하기 위해서는 damper를 사용하여 스프링의 길이가 변하는 속도를 제한한다.
• Damper
  -> 스프링의 길이가 빠르게 변화하기 시작할 때, damper는 시뮬레이션이 발산하지 않는 범위 내로 제어한다.
  -> spring damper는 객체의 형태를 안정적으로 만드는데 도움을 준다.
  ex) 인접한 면 사이에 특정각이 필요한 경우
  스프링 : rest angle 사이에 있는 면의 탈선을 방지, rest angle을 복원시키기 위해 edge를 따라 토크를 분리시킨다.
  damper : 움직임을 제한
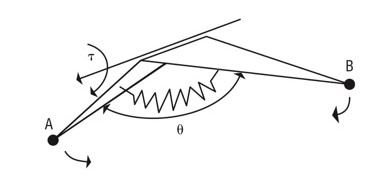  [토크를 복원시키는 스프링]

  $\tau = k_s(\theta(t)-\theta_r)-k_d\dot{\theta}(t)$

7.2.2 Virtual Spring

• 물리적 요소에서 직접 모델링 되지 않는 힘을 시스템에 도입하는 것이다.
  -> 객체의 움직임을 제어하는데 사용된다.
• rest length 가 0인 가상 스프링 : 한 객체가 다른 객체의 위에 놓여있는 제한이 있을 때 사용할 수 있다.
• PDC (Proportional derivative controllers) : 제어 변수와 그 미분치가 목표하는 값의 근방으로 유지되도록 하는 가상 스프링
  -> $\tau = k_s(\theta(t)-\theta_d)-k_d(\dot{\theta}(t)- \dot{\theta_d})$

7.3 Particle System

• 파티클 시스템의 공통적인 가정사항
  1) 파티클은 다른 파티클과 충돌하지 않음
  2) 집합적인 경우를 제외하고 파티클은 그림자를 만들지 않음
  3) 파티클은 서로 그림자를 만들지 않고, 환경(파티클이 없는)에만 그림자를 만듦
  4) 파티클은 조명을 반영하지 않음-파티클은 point light의 형태로 모델링 됨
• 파티클은 유한한 기간을 가진 것으로 모델링된다. (난수화를 통해 규칙성을 없앤다)
  1) 해당 프레임에서 임의의 새로운 파티클 생성
  2) 새로운 파티클에 속성 부여
  3) 자신에 할당된 생명 기간을 초과한 파티클은 종료
  4) 파티클 랜더링
  
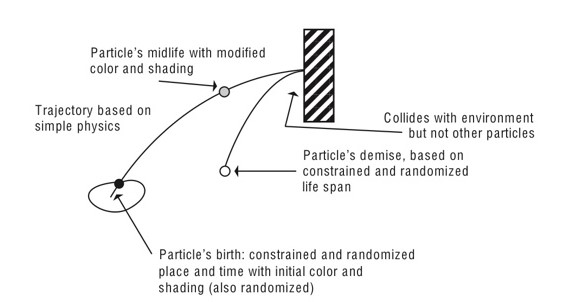
  [파티클 시스템의 생명 기간]

7.3.1 Particle Generation

• 파티클은 각 프레임 당 사용자가 원하는 파티클의 개수를 중심으로 사용자가 원하는 분포(균일, 가우스 등)를 사용하여 생성된다.
  -> #of particles $= n +Rand()*r$
  ($r$ : 원하는 범위로 scale)
  -> #of particles = $n(A) + Rand()*r$
  ($A$ : fuzzy object를 모델링 하는 경우 물체가 차지하는 화면의 영역)

7.3.2 Particle Attributes

• 파티클의 속성 : Position, Velocity, Shape Parameters, Color, Transparency, Lifetime
  -> 파티클의 속성은 파티클 시스템 내에서 동작상태, 외형, 수명 등을 결정한다.
  -> 각 속성은 파티클이 만들어 질때 초기화되며, 획일성을 피하기 위해 난수화한다.
  -> 위치와 속도 : 파티클의 동작에 따라 갱신
  -> 형태 보조변수, 색, 투명도 : 파티클의 외형 제어
  -> 수명 : 파티클이 몇 프레임동안 존재하는지 확인

7.3.3 Particle Termination

• 파티클은 새로운 프레임 마다 수명 속성이 하나씩 감소되고, 0이되면 종료(제거)된다.

7.3.4 Particle Animation

• 공간상에서 파티클의 위치를 움직이게 하기 위해서, 사용자는 힘을 고려하고 합성된 파티클의 가속도를 계산한다.
• 파티클의 속도는 가속도로 갱신되며, 해당 시점의 평균속도가 계산되어 파티클의 위치를 갱신한다. (중력, global force fields, local force fields, 충돌 등의 영향을 받음)
• 파티클의 색과 투명도는 파티클의 수명, 높이, 전역 시간등에 대한 함수로 표현할 수 있다.
• 파티클의 모양은 속도 함수가 될 수 있다.

7.3.5 Particle Rendering

• 랜더링을 단순화 하기 위해 파티클을 덮고 있는 픽셀에 색을 추가하여 point light 형태로 모델링 한다.

7.3.6 Particle System Representation

• 파티클은 튜플[x, v, f, m] 으로 표현된다.(위치, 속도, 힘, 질량)

typedef particle_struct struct
{
	vector3D 	p; 		//position
    vector3D 	v; 		//velocity
    vector3D 	f; 		//force accumulator
    float    	mass; 	//mass(질량을 가지는 튜플)
}particle

• 파티클의 상태 [x, v] 는 상미분방정식을 통해 [v, f/m] 로 갱신된다.
• 파티클 시스템은 시간 변수를 가진 파티클의 배열이다 [*p, n, t]

typedef particelSystem_struct struct
{
	particle 	*p; //각 파티클에 대한 상태 정보 배열
    int			n;  //파티클 수
    float 		t;  //파티클 시스템의 현재 시간(life)
}particleSystem

• 파티클 시스템의 갱신
  1) 모든 파티클에 대해 힘 벡터를 0으로 지정
  2) 모든 파티클에 대해 모든 힘의 합을 결정
  3) 배열로 모든 파티클의 상태를 가져옴
  4) 모든 파티클에 대한 갱신값 배열을 가져옴
  5) 상태 배열에 갱신된 배열 저장
  6) 새로운 상태 배열 저장
  7) 시간 변수 갱신

7.3.7 Forces on Particles

• unary Force : 중력, 점성의 drag
• Particle fair forces : 스프링과 댐퍼
  -> 파티클에 가능한 쌍에 대하여 힘을 계산하는 것은 비용이 많이 들기 때문에 '버킷정렬' 등을 통해 계산을 줄이는 것이 필요하다.
• envirnoment force : 파티클에 미치는 중력, 바람, 공기 점도 및 충돌과 같은 환경

7.3.8 Particle Life Span

• 파티클 자료구조는 파티클 시스템이 시뮬레이션을 하는데 필요한 수만큼 재사용된다.
  -> 초기값은 사용자가 제어하는 정도로 생성되지만, 유일성을 피하기 위해 난수 값을 사용한다.

7.4 Rigid Body Simulation

• 강체 시뮬레이션 갱신 사이클
  1) 객체 특성(위치,선형속도,각속도,운동량..)
  2) 힘을 계산(중력, 점성..)
  3) 객체의 질량으로부터 가속도 계산
  4) 객체의 위치, 속도, 운동량의 변화 계산
  다시 1) 로 돌아감
• 강체 시뮬레이션의 문제점 : 연속적인 처리의 모델링을 이산적인 시간 간격을 통해 모델링 해야한다는 점
• 표준 물리학 : 객체가 의미있는(땅에 부딪히는 등) 이벤트가 발생한 특정한 시간의 움직임을 분석
• 컴퓨터 애니메이션 : 중요 이벤트와 그 이벤트와 함께 이산적인 시간에서 객체의 움직임을 모델링 하는 것

7.4.1 Bodies in Free Fall

• 이산적인 시간 간격에서 시작 위치, 속도, 가속도의 관점에서 갱신된 위치
  (시간간격 주기 $\Delta t$ 일때 점의 위치 $x(t)$, 속도 $v(t)$, 가속도 $a(t)$)
  -> $x(t+\Delta t)=x(t)+v(t)*\Delta t+\frac{1}{2}*a(t)*\Delta t^2$

• 가속도가 Delta 시간 간격동안 상수 값으로 남아있다는 가정은 강체 시뮬레이션에 있어서 정확하지 않다.
  -> $\Delta t$에 의한 시간 단계의 시작시에 $\Delta t$를 곱하여 이를 가속도와 다음 속도를 곱함(오일러 적분 방식)
  -> 시간 단계를 작게 만들면 이상적인 경로와 유사해 질 수 있지만, 계산 비용이 증가하게 된다.
  
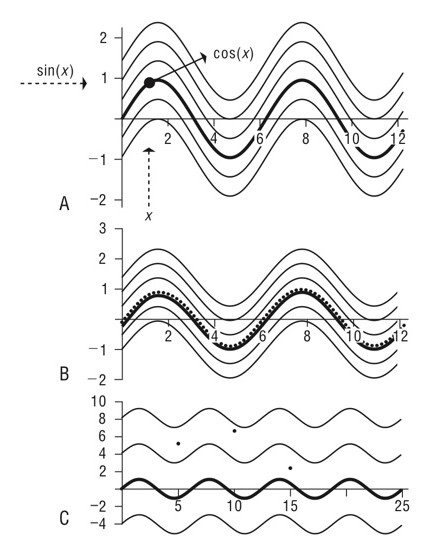
  [A는 이상적인 결과 값 / B는 $\Delta x=0.2$인 경우(이상적인 값과 유사) /C는 $\Delta x=5$인 경우(이상적인 값과 차이가 생김)]
  -> 적분을 이용한 이차Runge-Kutta 방식과 중간점 방식은 큰 시간 단계를 이용하더라도 정확한 결과가 나온다.
  
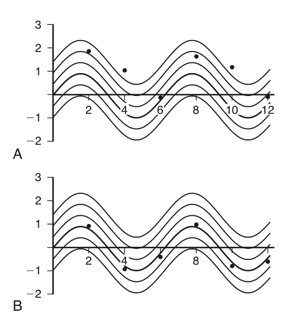
  [단계 크기가 2일때 A는 오일러 방법, B는 중간점 방법 -> B가 더 정확한 결과]

• 강체를 위한 움직임 수식
  -> 힘이 객체의 질량중심에 직접 작용하지 않을 경우 선형힘, 토크를 고려해야 한다.
  -> 객체에 작용함으로써 초래되는 움직임을 유일하게 구하기 위해서 선운동량과 각운동량이 보존되어야 한다.
  -> 최종적인 각운동량을 구하기 위해서 공간상에서의 객체 질량 분포나 interia tensor에 의해 특징지어진다.

• 방위와 회전 운동량
  -> 위치, 속도, 가속도의 선형 속성과 유사하게 3차원 객체는 방위, 각속도, 시간에 대한 함수 형태인 각 가속도의 회전 속성을 가지고 있다. (파티클-공간상의 개별적인 점 모델링-의 경우 회전 정보 무시)
  -> 각 가속도 벡터의 크기 = 회전 속도 / 각속도 벡터의 크기 = 단위 시간당 회전 속도
  
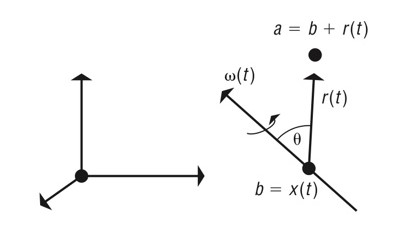
  [축에 대한 점 a의 회전]
  -> $\dot{r}(t)=\omega(t)\times r(t)$ ($\omega(t)$ : 각속도)
  -> $\left\vert \dot{r}(t) \right\vert=\left\vert \omega(t) \right\vert\left\vert r(t)\right\vert\sin\theta$
  [공간상에서 범위를 가진 객체를 고려]
  -> $\dot{R}(t)=\omega(t)*R(t)$
  [강체 객체에 있는 한점 Q를 고려]
  (객체의 지역 공간에서 위치q, world 좌표계에서 위치 q(t) 공간상에서 body의 위치 x(t), body의 방향 R(t))
  -> $q(t)=R(t)q+x(t)$
  -> $\dot{q}(t)=\omega(t)*R(t)q+v(t)$
  -> $\dot{q}(t)=\omega(t)\times((q(t)-x(t))+v(t)$

• 질량중심
  -> 컴퓨터 그래픽스 분야에서 객체의 질량 분포는 개별적인 점으로 모델링 되며, 대부분 질량 값을 각 객체의 정점에 부여하는 방식으로 구현된다.
  -> 객체 전체 질량 : $M=\sum m_i$ ($m_i$ : 개별질량)
  -> 질량 중심 : $x(t) = \frac{\sum m_iq_i(t)}{M}$ ($x(t)$ : 객체의 질량중심, $q_i(t)$ : world 공간에서의 점)

• 힘
  -> 한 점에 미치는 다양한 힘은 전체 외부의 힘이 합쳐진 형태인 $F(t)$로 표현된다.
  -> $F(t) = \sum f_i(t)$

• 운동량
  -> 객체의 운동량은 선형 요소와 각 요소로 분해된다.
  -> 선형 운동량 : 강체의 작용하는 힘이 운동량의 변화와 동일
  $p=mv$
  $P(t) = \sum m_i\dot{q}_i(t)$ ($P(t)$ : 강체의 전체 선형 운동량)
  $P(t)=Mv(t)$
  $\dot{P}(t)=M\dot{v}(t)=F(t)$
  -> 각 운동량 : 객체를 구성하는 질량점의 합(각운동량이 객체 운동의 선형요소에 직접적 의존 x)
  $L(t)=\sum ((q(t)-x(t))\times m_i(\dot{q}(t)-v(t)))$
  $=\sum(R(t)q\times m_i(\omega(t)\times(q(t)-x(t))))$
  $= \sum(m_i(R(t)q\times(\omega(t)\times R(t)q)))$
  $\dot{L}(t)=\tau(t)$ : 토크는 각 운동량의 변화와 같다
  -> 상수 각운동량을 유지시키기 위해서 질량의 거리가 감소할 때 각 가속도는 증가해야 한다.

• Interia Tensor
  -> 선형 운동량이 선형속도와 연관성이 있는 것과 동일하게 각운동량은 각속도와 연관되어 있다.
  $L(t) = I(t)w(t)$ ($I$ : 초기 관성 텐서)
  -> 관성 텐서는 시간에 의존적이다.

7.4.2 Bodies in Collision

• 충돌 물체

  • 충돌 발생 검출 : 객체의 위치와 방향이 시간에 따라 변하는 모습 - kinemaic
    -> 한 객체의 움직임을 다른 객체에 대해 상대적으로 고려
    -> 두 객체의 교차가 있는지를 검사
  • 충돌에 대한 적절한 계산 : 힘의 충돌을 계산하여 새로운 움직임 만들기 - dynamic
    -> 충돌 반응 : 객체의 기하학적인 크기보다 질량의 분포가 중요
    • 충돌 반응의 방법 1 - Kinematic Response
      -> 빠르고 편리, 파티클과 원구형 물체에 적합
    • 충돌 반응의 방법 2 - Penalty Method
      -> 계산 편리, 강체 움직임을 시뮬레이션하는 계산적 구조로 통합될 수 있음
    • 충돌 반응의 방법 3 - Calculating Impulse Force
      -> 정밀한 방법, 첫 충돌점으로 거슬러 올라가는 방식
    -> 충돌 시간 :
    1) 충돌에 포함된 파티클의 반작용 계산
    2) 다수의 충돌 발생 시 첫 충돌이 발생한 시점으로 돌아감(역추적)

• 파티클-평면 충돌과 운동학적 반응(Kinematic Response)
  
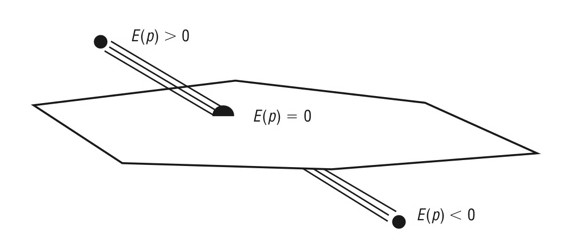
  [파티클이 평면과 충돌하는지에 대한 판별]
  $E(p)=ap_x+bp_y+cp_z+d=0$
  -> $p(t_i)=p(t_{i-1})+v_{ave}(t)\times \Delta t$
  $E(p)>0$ 인 경우 평면의 전면에 존재하고 $E(p)<0$인 경우 평면 후면에 존재한다.
  -> 시간 간격마다 파티클이 평면 정면에 있는지 검사하고, 계속해서 양수라면 충돌이 없는 것이다.
  -> $E(p(t_i))$의 값이 음수가 될때 $t_{i-1}$과 $t_i$ 사이에서 충돌이 발생한 것
  -> 충돌이 일어난 후에 처리(제동 인자 적용)
  $v(t_{i-1})=v(t_i)-v(t_i)N-kv(t_i)N$
  $=v(t_i)-(1-k)v(t_i)N$

• 벌점 방식(The Penalty Method)
  -> 객체 내의 충돌에 대한 반작용을 만드는 기법
  -> 임의의 질량이 점에 부여되고, 임의의 상수가 스프링을 위해 결정되어야 한다.
  -> 다면체 객체의 경우 토크가 발생한다.

• 다면체의 검사(Testing Planer Polyhedra)
  -> bounding box test (최소-최대 검사) : x,y,z,값중 최소 최대를 이용
  -> bounding sphere or bounding slabs test : 객체의 모양이 상자와 맞지 않을 때

  • 대부분의 경우
    1) 한 객체의 모든 정점에서 한 정점이 다른 다면체의 내부에 있는지 검사
    2) 다른 객체의 각 정점이 첫 객체의 내부에 있는지 검사
  • 오목 다면체의 경우
    semi-finite 광선을 통해 검사
    -> 한 점에서 특정한 한 방향으로 광선을 쏘고 해당 광선이 모든 면과의 교차횟수를 측정
    -> 홀수 : 점이 객체 내부에 있는것 / 짝수 : 외부에 있는것
  • 선분-면 검사(예외 체크)
    -> 각 객체의 선분이 다른 객체의 모든 면과 만나는 경우, 혹은 그 반대의 경우를 체크

• 충돌시의 충격력(Impulse Force of Collision)

  • 정밀한 충돌시 반응을 처리하기 위해서, 충격 시점으로 시간을 거슬러 올라가 해당 시간에서 반작용을 계산한다.

  • 밀접한 공간에서 다수의 충돌이 발생했을 때에는 계산비용이 매우 증가한다.

  • 점-평면 충돌시, 각속도를 무시할 수 있어 충격을 간략화 시킬 수 있다.
    ex) 충돌이 $t_{i-1}$과 $t_i$사이에서 발생 - 충돌이 발생한 정확한 시간 t 찾기
    -> 각 시간은 검사 시간 간격의 하한값과 상한값이 된다.
    -> 각 검색 반복 시 점의 위치는 시간 간격의 중간값이 된다.(만약 충돌이 없었다면, 상한값이 중간값으로 대체 반대의 경우는 하한값이 중간값으로 대체)
    -> 목표한 허용치 값을 얻을 때 까지 지속
    => 계산을 단순히 하기 위해 상수 속도 근사화 이용가능
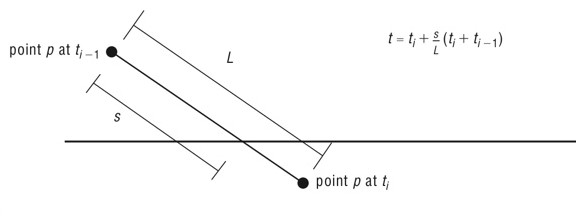    [충격시간 t의 예측-상수 속도 근사화]

  • 충격시 점의 속도의 법선 요소는 충돌에 의한 반응으로 수정될 수 있다.
    충돌시 탄성 정도를 모델링하여 속도를 얻는데 복원력 계수를 적용할 수 있다.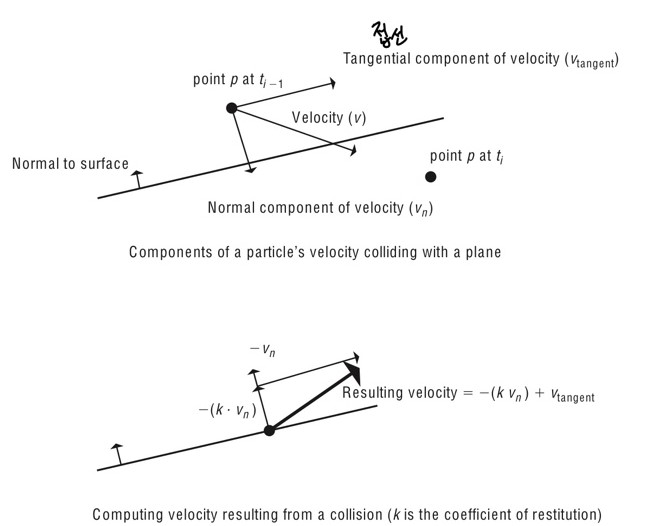
    [평면과 점의 충돌 결과($k$ : 복원력 계수)]

• 충격력의 계산(Computing Impulse Forces)
  -> $J=F\Delta t$ ($J$ : 충격력)
  -> $J=F\Delta t =Ma\Delta t=M\Delta v=\Delta (Mv)=\Delta P$
  -> $v^+_{rel}(t)=-k v^-_{rel}(t)$ ($k$ : 0과 1 사이의 값인 회복력 계수)

  • 두 객체 A,B의 충돌이 시간 t에서 검출되었을 때
    -> 질량중심 $(x_A(t), x_B(t))$, 선형속도$(v_A(t),v_B(t))$, 각속도$(w_A(t),w_B(t))$, 질량 중심에 대한 접촉점에 대한 상대적인 위치 $r_A, r_B$, 충돌점 $P_A,P_B$
    
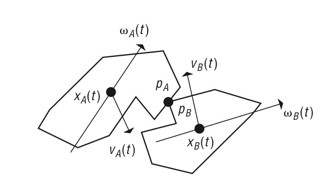
    [충돌하는 객체의 상대적 배치]
    $r_A=P_A-x_A(t)$
    $r_B=P_B-x_B(t)$
    $v_{rel}(t)=((\dot{p}_A(t)-\dot{p}_B(t))\bullet N)N$
    $\dot{P}_A(t)=v_A(t)+\omega_A(t)\times r_A(t)$
    $\dot{P}_B(t)=v_B(t)+\omega_B(t)\times r_B(t)$
  • 충돌 이전 객체의 선속도와 각속도$(v^-,w^-)$ 는 충돌 후 의 선속도와 각속도$(v^+,w^+)$로 갱신되고, 충격력은 접촉면의 법선 방향의 벡터량이다.
    
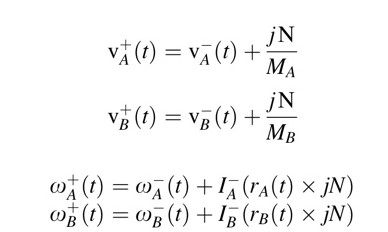
  • 충격력을 얻기 위해서 충격면의 법선 방향에서 충돌 이후 접촉면의 속도차이를 구하고, 이전에 구한 식을 이용하여 j에 대한 식을 구할 수 있다.
    
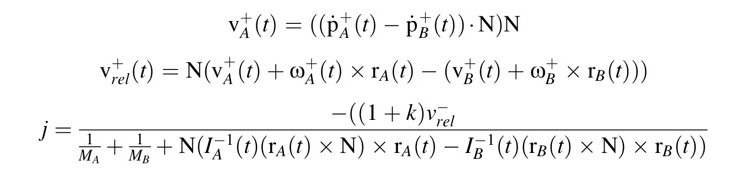
    -> 두 객체 사이의 접촉은 접촉면의 법선 벡터와 접촉면에 포함된 각 객체의 점에 의해 정의된다.
    -> 접촉점은 실제 충돌이 발생하는지 검사를 위해 존재
    -> 충돌이 있을 경우 위에서 구한 j에 대한 식을 이용하여 충격력의 크기를 계산한다. 이후 이 충격력은 접촉면의 법선 크기 변화에 다시 사용되고, 법선은 각 객체의 운동량과 각 운동량을 갱신한다.
    -> 충돌이 발생하지 않을때 까지 반복한다.

• 마찰력

  • 정지하고 있을 때(정지마찰력에 의해 임계힘을 가진다)
    $F_s$ : 정지 마찰력, $F_N$ : normal force, $\mu_s$ : 정지 마찰력 계수
    -> $F_s=\mu_sF_N$
  • 객체가 움직일 때(운동 마찰력 생성)
    ->$F_k=\mu_kF_N$

• Resting Contact
  ???

7.4.3 Dynamics of Linked Hierarchies

• 제한된 역학
  -> Geometric point constraints는 강체 역학 대신 사용할 수 있다.
  ex) 파티클은 거리 제한조건을 연결
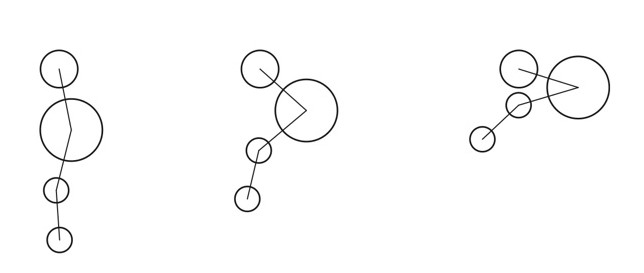  [큰 구에 의해 작은 구는 거리 제한조건을 만족시키기 위해 움직이는 모습]
• 페더소톤 방정식
  -> four hierarchy-traversal loops
  1) 링크 속도를 초기화(루트로부터 바깥 방향으로)
  2) 링크 값을 초기화(루트로부터 바깥 방향으로)
  3) 값을 갱신(끝단부로부터 내부 방향으로)
  4) 가속도 계산(루트로부터 바깥 방향으로)

7.5 Enforcing Soft and Hard Constraints

• 물리기반 애니메이션에서 가장 큰 문제는 객체에 대하여 애니메이터과 원하는 작업과 함께 객체가 주변 환경 속에 존재하는 힘에 대한 반작용을 함께 모델링 하는 일이다.
• 해결책으로 해당 객체의 움직임에 대한 DOF의 제약조건을 두는 것이다
  제약조건은 동일 지점의 점, 객체간의 최소거리 유지, 공간상의 특정한 방위 가지도록 요구 등으로 나타난다.
• hard constraints : 모든 제약조건을 만족시키는 동시에, 시스템 내부의 힘에 반응하는 움직이는 계산을 해야한다. -> 더 많은 조건이 추가될수록 복잡하다.
• soft constraints : 최종적인 움직임에 영향을 주는 추가적인 힘, 시스템 내에 더해지는 값이다.

7.5.1 Energy Minimization

-> 에너지 함수는 점을 공간상에서 보간하기 때문에 객체를 함께 고정시키거나, 객체의 형태를 복구, 스플라인 내의 곡률 최소화 등에 사용된다.
-> 에너지 제약 조건은 모델 보조변수의 임의 함수에 기초하여 힘의 복구를 유도한다. (모델의 현재 상태는 보조변수 값의 집합($\Psi$)으로 표현된다)
-> 음이 아닌 smooth 함수에서 제약조건은 $E(\Psi)$로 표현된다.
-> 초기 보조변수 집합 $\Psi_0$에서 시간 0에서의 매개변수 함수는 $F(0)=\Psi_0$형태로 정의된다.
-> 오일러의 공식에 의해 $F(t_{i+1})=F(t_i)-h\nabla E$ 로 표현되고, 매개변수 함수는 $(d/dt)F(t)=-\nabla E$ 를 만족한다.

• 세가지 유용한 함수
  1) 매개 변수화 된 위치함수 : $P(u,v)$
  2) 곡면 법선 벡터 함수 : $N(u,v)$
  3) 음함수 : $I(x)$
• 유용한 제약조건
  • Point-to-Fixed-Point
    ->점 Q는 고정, 점 P는 모델 곡면위의 특정한 점 두 점이 만날 경우 에너지 함수는 0이 된다.
    -> $E=\left\vert P(u,v)-Q \right\vert^2$
  • Point-to-Point
    -> 곡면위의 두 점 두 점이 만날 경우 에너지 함수는 0이 된다.
    -> $E=\left\vert P^a(u_a,v_a)-P_b(u_b,v_b) \right\vert^2$
  • Point-to-Point Locally Abutting
    -> 두 점이 만나고 해당 점에서 법선 벡터의 내적이 -1과 같을 경우 에너지 함수는 0이 된다(서로 떨어져서 서로를 가리키는 경우)
  • Floating Attachment
    -> 객체 b의 음함수를 사용, 객체 a의 특정 점이 객체 b 곡면위에 놓인다.
    -> $E = (I^b(P^a(u_a,v_a)))^2$
  • Floating Attachment Locally Abutting
    -> Floating Attachment의 조건을 만족하고, 객체 a의 법선 벡터와 점은 반드시 객체 b의 접촉점의 법선 벡터와 방향이 반대이고 동일 선분에 있어야 한다.
  • Energy Constraints Are Not Hard Constraints
    -> 에너지 함수가 쉽게 구현가능하고 효과적으로 사용할 수 있지만, 단점은 모델에 부여된 제약조건이 항상 hard constraints가 아니라는 것이다.

7.5.2 Space-Time Constraints

• 공간-시간 제약조건은 움직임을 공간상에서 시간간격동안 발생하는 제한된 최적화 문제의 해로 간주한다.