동적 계획 (dynamic programming)

• divide and conquer
  • 하향식 해결법
  • 나누어진 부분들이 서로간의 상관관계가 없는 문제를 해결하는데 적합
  • ex) 피보나치 계산의 경우 나누어진 부분들이 상관관계가 있기 때문에 divide and conquer 방식이 적합하지 않다.
• dynamic programming
  • 상향식 해결법 (큰 문제를 작은 문제로 나눠서 해결)
  • 인덱스를 효과적으로 설정하여 작은 문제들의 중복해결을 없앤다.
  • 개발 절차
    1) recursive property 정립
    2) 작은 문제를 해결해서 큰 문제로 나아가는 상향식 방법으로 진행

1. 이항계수 구하기

<divide and conquer 방식>

• $n \choose k$ 를 0<k<n 에서 $n-1 \choose k-1$ + $n-1 \choose k$와 k=0 or k=n에서 1로 나눠서 계산
• pseudo code

int bin(int n, int k)
{
	if(k == 0 || n == k)
    	return 1;
    else
    	return bin(n-1,k-1) + bin(n-1,k);
}

시간복잡도 분석

• 분할정복 알고리즘을 사용한 경우 재귀호출에 있어서 같은 계산이 반복된다.
• $_{n}\mathrm{C}_{k}$ 를 구함에 있어서 계산하게 되는 총 항의 갯수는 $2\times _{n}\mathrm{C}_{k}-1$ 이다.

<dynamic programming 방식>

• recursive property 정립
  $B[i][j] = \begin{cases} B[i-1][j-1]+B[i-1][j], & 0<j<i \\ 1 & j=0 \ or\ j=i \end{cases}$
• B[0][0]를 먼저 구한 후 i와 j를 키워가면서 계산하면 된다. (by 파스칼의 삼각형)
• 동적계획법을 사용한 이상계수 계산 코드 (python)

def bin2(n,k):
    B = [[0 for i in range(k+1)] for j in range(n+1)]
    for i in range(n+1):
        for j in range(min(i,k)+1):
            if(j==0 or j==i):
                B[i][j] = 1
            else:
                B[i][j] = B[i-1][j-1] + B[i-1][j]
    return B[n][k]

동적계획 알고리듬 분석

• $_{n}\mathrm{C}_{k}$를 구하는 동작 예시
  • i : 0,1,2,3, ..., k, k+1, ..., n
  • j루프의 수행횟수 : 1,2,3,4, ..., k+1,k+1, ..., k+1
  • 즉 $_{n}\mathrm{C}_{k}$를 구할 때 k 값보다 큰 것들은 계산할 필요가 없다.
• 총 수행횟수
  • $1+2+3+...+k+(k+1)+...+(k+1)$ 여기서 k+1은 n-k+1 번 더한다.
  • = $\frac{k(k+1)}{2} + (n-k+1)(k+1)$
  • = $\frac{(2n-k+2)(k+1)}{2} \in \Theta(nk)$

2. 그래프

2-1. 최단경로 문제 (All-Pairs shortest paths problem)

• 한 도시에서 다른 도시로 갈 수 있는 가장 짧은 길을 찾는 문제
  

무작정 알고리즘(brute-force algorithm)

• 정점에서 다른 정점으로 가는 가능한 모든 경로들의 길이를 구한 뒤, 최소길이의 경로 찾기
• 주어진 그래프가 n개의 정점을 가지고 모든 정점들 사이에 edge가 있다고 가정
  • 정점 $v_i$에서 $v_j$로 간다고 했을 때 모든 정점을 거치는 경우 거쳐갈 수 있는 정점의 수를 생각해 보자
  • $v_i$에서 출발하여 다음에 도달할 수 있는 정점의 가지 수는 $n-2$ (출발, 도착 빼기)
  • 다음 정점을 선택하면 다음의 가지수는 $n-3$ 그다음은 $n-4$ 이렇게 계속 작아진다.
  • 결론적으로 총 경로의 수는 $(n-2)!$
  • 이 경우는 모든 정점을 거치는 경우로 모든 정점을 거치지 않는 경우까지 계산하면 계산이 매우 많아진다. -> 비효율적이다.

동적 계획식 설계

• 그래프의 인접행렬식 표현: $W$
  $W[i][j]= \begin{cases} edge\ 의\ 가중치 & v_i에서\ v_j로\ 가는\ edge가\ 있는\ 경우 \\ \inf & v_i에서\ v_j로\ 가는\ edge가\ 없는\ 경우 \\ 0 & i=j\ 인\ 경우 \end{cases}$
• 그래프에서 최단경로의 길이 표현
  $D^{(k)}[i][j]$ : 집합 $\left\{ v_1,v_2,v_3,..v_k \right\}$의 정점들 만을 이용해서 $v_i$에서 $v_j$로 가는 최단경로의 길이
• ex1) $D^{(0)}[i][j] = \varnothing$
• ex2) $D^{(1)}[i][j]$ = $\left\{ v_1 \right\}$

동적 계획식 설계절차

• recursive property 정립
  $D^{(k)}[i][j] = minimum \left\{D^{(k-1)}[i][j],\ D^{(k-1)}[i][k]+D^{(k-1)}[k][j] \right\}$
• 경우1) $D^{(k-1)}[i][j]$
  • $\left\{ v_1,v_2,v_3,..v_k \right\}$ 의 정점들 만을 통해서 $v_i$ 에서 $v_j$ 로 가는 최단경로가 $v_k$ 거치지 않는 경우
• 경우2) $D^{(k-1)}[i][k]+D^{(k-1)}[k][j]$
  • $\left\{ v_1,v_2,v_3,..v_k \right\}$ 의 정점들 만을 통해서 $v_i$ 에서 $v_j$ 로 가는 최단경로가 $v_k$ 거치는 경우
• 상향식으로 $D^{(0)}$에서 $D^{(n)}$ 까지 계산

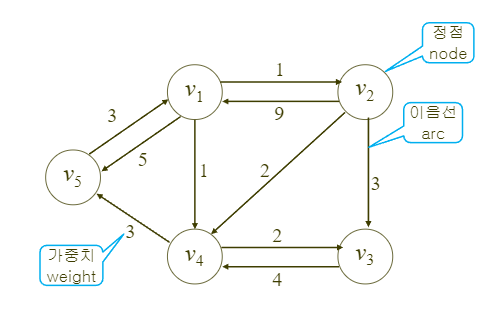
예시(위의 그림 사용)

• $D^{(1)}[2][4]$ : $min(D^{(0)}[2][4],\ D^{(0)}[2][1]+D^{(0)}[1][4]) = min(2,9+1) = 2$
• $D^{(1)}[5][2]$ : $min(D^{(0)}[5][2], D^{(0)}[5][1]+ D^{(0)}[1][2]]) = min(\inf, 3+1) = 4$
• ...생략...
• $D^{(1)}$을 모두 계산한 후 $D^{(2)}$ 를 계산한다. 이후 순차적으로 $k$를 늘려가며 계산

Floyd의 알고리즘 I

• Pseudo Code

void floyd(int n, const number W[][], number D[][])
{
	int i, j, k;
    D = W;
    for(k = 1; k <= n; k++)
    	for(i = 1; i <= n; i++)
        	for(j = 1; j <=n; j++)
            	D[i][j] = mininum(D[i][j], D[i][k] + D[k][j]);
}

• 가능한 모든 경우를 분석
  $T(n) = n*n*n = n^3 \in \Theta(n^3)$

Floyd의 알고리즘 II

• 추가공간 필요없이 D만을 이용하여 데이터 저장
• k번째 행과 k번째 열에 있는 값들이 루프의 k번째 반복을 수행하는 동안 변하지 않기 때문
  -> D[i][k] = min(D[i][k], D[i][j] + D[k][k]);
  -> D[k][j] = min(D[k][j], D[k][k] + D[k][j]);
  에서 D[k][k] = 0 이므로 D[i][k] = D[k][j] 이게 된다.
• Pseudo Code

void floyd2(int n, const number W[][], number D[][], index P[][])
{
	index i, j, k;
    for(i=1; i<=n; i++)
    	for(j=1; j<=n; j++)
        	P[i][j] = 0;
    D = W;
    for(k=1; k<=n; k++)
    	for(i=1; i<=n; i++)
        	for(j=1; j<=n; j++)
            	if(D[i][k] + D[k][j] < D[i][j])
                {
                	P[i][j] = k;
                    D[i][j] = D[i][k] + D[k][j];
                }
    
}

2-2. 최적의 원칙

• 어떤 문제 사례에 대한 최적의 해가 그 사례의 부분사례에 대한 최적의 해를 항상 포함하고 있으면, 최적의 원칙이 적용된다라고 한다.
• 최적의 원칙이 적용되어야 동적 계획법을 사용할 수 있다.
• 쉽게 말해서 전체가 최적이면, 부분도 최적이다.
• 그러나 모든 문제가 최적의 원칙을 따르는 것은 아니다.

2-3. 연쇄 행렬 곱셈

• 기본적으로 i x j 행렬과 j x k 행렬을 곱하기 위해서는 i x j x k 번 곱셈이 필요하다.
• 그러나 연쇄적으로 행렬을 곱할 때, 곱하는 행렬의 순서에 따라 총 곱셈 횟수가 달라진다.
  -> 횟수가 가장 적게되는 최적의 순서 결정하기!

연쇄 행렬 곱셈 무작정 알고리즘

• 가능한 모든 순서를 고려하고, 가장 최소인 것을 택하기
• 예를들어 n개의 행렬이 있고, 곱할 수 있는 모든 순서의 가지수가 $t_n$ 일 때
  $A_1$이 마지막으로 곱하는 행렬일 경우 나머지 행렬을 곱하는 것에는 $t_{n-1}$가지수가 존재한다. 반대로 $A_n$을 마지막으로 곱할 때도 $t_{n-1}$가지수가 존재한다.
  -> 이것을 통해 $t_n \ge t_{n-1} + t_{n-1} = 2t_{n-1}$이고 $t_2=1$이다.
  -> $t_n\ge 2t_{n-1}\ge 2t_{n-1}^2 \ge 2t_{n-1}^3 \ge ...\ge 2_{t_2}^{n-2} = 2^{n-2}∈Θ(2^n)$
• 무작정 알고리즘의 모든 가능한 가지수 $P(n)$
• $P(n) = C(n-1)$
  $C_n=\frac{1}{n+1}$$2n \choose n$
  • ex1) 4개의 행렬을 곱하는 경우의 수
    $P(4) = C(3) = \frac{1}{3}$$6 \choose 3$ = $\frac{1}{4} \times 20=5$
    cf) 이진트리 : 노드 3개로 구성
  • ex2) 5개의 행렬을 곱하는 경우의 수 : 앞에서 계산한 것을 이용하게 된다.
    -> 최적의 원칙

연쇄 행렬 곱셈 동적계획식 설계전략

• $M[i][j]$ : $i\le j$일때 $A_i$에서 $A_j$ 까지의 행렬을 곱하는데 필요한 곱셈 횟수
  $A_k$의 크기는 $d_{k-1}\times d_k$ (각각 행, 열 의 수)
  $M[i][j] = \begin{cases} min_{i\le k\le j-1}(M[i][k] + M[k+1][j] + d_{i-1}d_kd_j) & if\ i<j \\ M[i][i] = 0 \end{cases}$
  $M[i][k]$ : $A_iA_{i+1}...A_{k}$
  $M[k+1][j]$ : $A_{k+1}...A_{j}$

최소 곱셈 알고리즘 (동적 계획식 설계전략)

• n개의 행렬을 곱하는데 필요한 기본적인 곱셈의 횟수의 최소치를 결정하고, 최소치를 구하는 순서 결정하는 문제
• Pseudo Code

int minmult(int n, const int d[], index P[][])
{
	index i, j, k, diagonal;
    int M[1...n][1...n];
    
    for(i=1; i<=n; i++)
    	M[i][j]=0;
    for(diagonal=1; diagonal<=n-1; diagonal++)
    	for(i=1; i<=n-diagonal; i++)
        	j = i + diagonal;
            M[i][j] = min(M[i][k] + M[k+1][j] + d[i-1]*d[k]*d[j]; //k는 i에서 j-1까지
            P[i][j] = 최소값이 되는 k값
    return M[1][n];
}

최소곱셈 알고리즘의 모든 경우분석

• 분석
  $j=i+diagonal$이므로
  -> $k$ 루프 횟수 : $(j-1)-i+1=i+diagonal-1-i+1=diagonal$
  $for-i$ 루프 횟수 : $n-diagonal$
  따라서
  $\sum_{diagonal=1}^{n-1}[(n-diagonal)\times diagonal]=\frac{n(n-1)(n+1)}{6} \in \Theta(n^3)$

2-4. 최적 이진검색 트리

• 이진검색트리에 데이터를 빠르게 찾을 수 있도록 구성하는 방법 찾기
• Optimal binary search tree : 키를 찾는데 걸리는 평균시간이 최소가 되도록 구축된 트리
• notation
  $p_i$ : $Key_i$가 검색키일 확률
  $c_i$ : 주어진 트리에서 $Key_i$를 찾는데 필요한 비교횟수
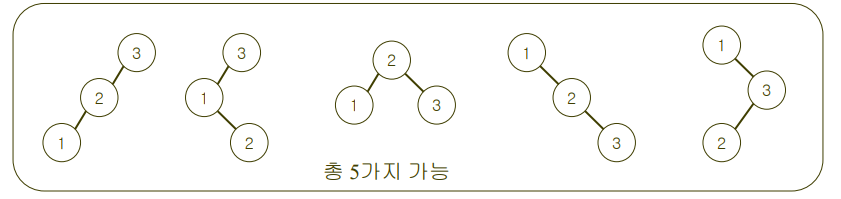
  평균검색시간 : $\sum_{i=1}^nc_ip_i$
• n=3 키가 1,2,3 인 경우 가능한 이진검색 트리의 종류
  
• n개의 키가 있는 경우 가능한 이진검색트리의 종류
  $C_n=\frac{1}{n+1}$$2n \choose n$ -> 너무 많은 계산을 해야함 -> 동적 계획법 사용!

동적계획법을 통한 최적 이진검색 트리 구성

• 목표
  $\sum_{m=1}^jc_mp_m$ 을 최소화하기
  검색시간의 최적값을 A[i][j] 로 표현 (A[i][j] = $p_i$)
• 중요 내용
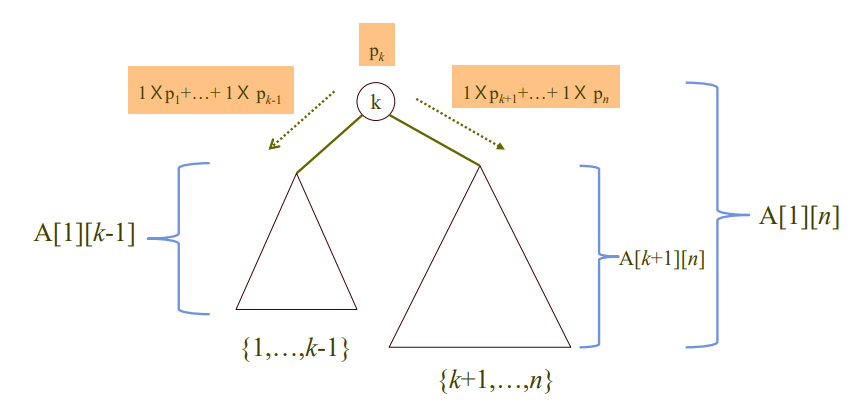
  • 트리 $k$ : n개의 키가 있을 때 이 중 $k$번째 키가 루트가 되는 트리
  • 트리 $k$의 검색시간 A[1][n]
    = $A[1][k-1] \\ +p_1+...+p_{k-1}\\ +p_k\\ +A[k+1][n]\\ +p_{k+1}+...+p_n\\ =A[1][k-1]+a[k+1][n]+\sum_{m=1}^np_m$
  • 맨 위에서부터
    • 왼쪽 부분트리에서 평균시간
    • 뿌리에서 비교하는데 드는 추가시간 (왼쪽으로 내려가는 시간)
    • 뿌리를 검색하는 평균시간
    • 오른쪽 부분트리에서 평균시간
    • 뿌리에서 비교하는데 드는 추가시간 (오른쪽으로 내려가는 시간)
  • 결론 : 최적의 이진검색트리 평균검색시간은
    $A[i][j] = min_{1\le k\le n}(A[i][k-1]+A[k+1][j])+\sum_{m=1}^np_m$
  • 그림으로 나타내면
    
• Pseudo Code (최소곱 코드와 유사함)

void optsearchtree(int n, const float p[], float& minavg, index R[][])
{
	index i, j, k, diagonal;
    float A[1..n+1][0..n];
    
    for(i=1; i<=n; i++)
    {
    	A[i][i-1] = 0;
        A[i][i] = p[i];
        R[i][i] = i;
        R[i][i-1] = 0;
    }
    A[n+1][n] = 0;
    R[n+1][n] = 0;
    for(diagonal=1; diagonal<=n-1; diagonal++) //#1
    {
    	for(i=1; i<=n-diagonal; i++) //#2
        {
        	j = i+diagonal; 
            A[i][j] = min(A[i][k-1]+A[k+1][j]+p) //k와 p는 i에서 j까지 반복 #3
            R[i][j] = 최소가 되는 k
        }
    }
    minavg = A[1][n];
}

시간복잡도 분석

$\sum_{diagonal=1}^{n-1}[(n-diagonal)\times(diagnoal+1)]=\frac{n(n-1)(n+4)}{6}\in \Theta(n^3)$
-> sum 동작은 의사코드의 #1, $n-diagonal$은 #2, $j-i+1=i+diagonal-i+1=diagonal+1$ 은 #3 의미

3. DNA 서열맞춤

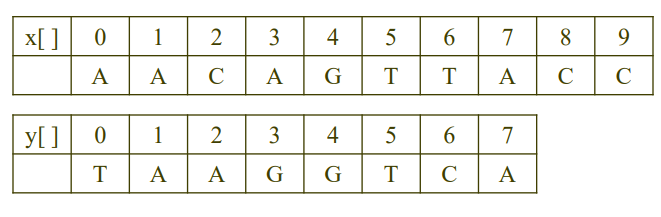
• 두개의 DNA 서열이 있을때 틈(2의 손해)과 불일치(1의 손해)에 대한 손해값을 정의하고, 비용을 계산하기
  
• opt(i,j) : 부분서열 x[i,...,9]와 y[j,...7]의 최적 맞춤 비용
  -> 결과적으로 구하려는 것은 opt(0,0)

최적의 원칙 이용

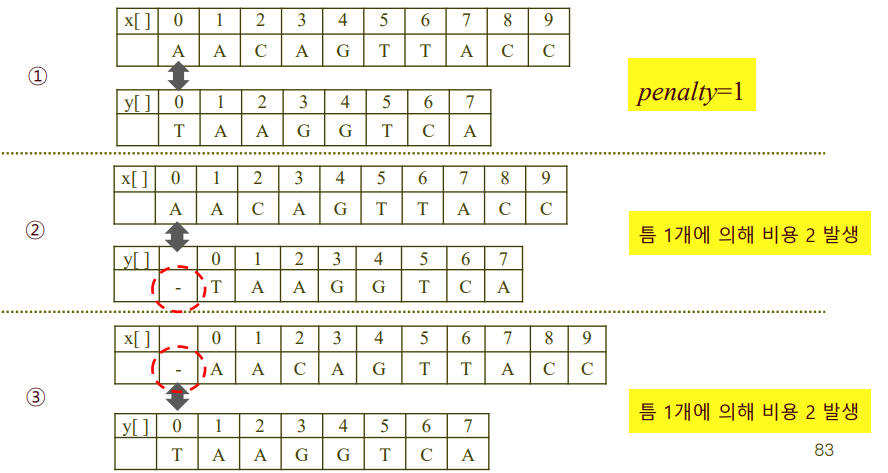
• 예시
  opt(0,0) = min(opt(1,1) + penalty, opt(1,0)+2, opt(0,1)+2), penalty는 불일치 할때 1, 일치하면 0
  opt(1,1) + penalty => (1)
  opt(1,0)+2 => (2)
  opt(0,1)+2 => (3)
  
• 일반식
  opt(i,j) = min(opt(i+1,j+1)+penalty, opt(i+1,j)+2, opt(i,j+1)+2)