탐욕적인 방법(Greedy Algorithm)
1. Intro
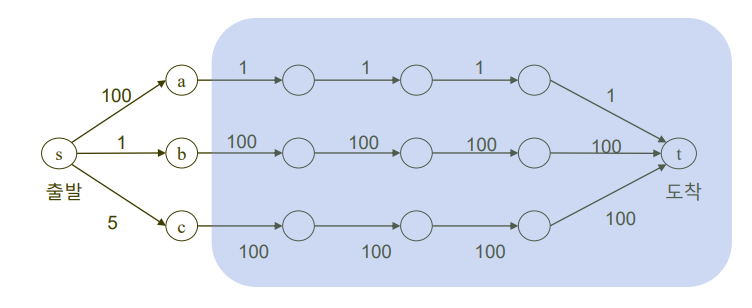
- 출발 지점에서 도착지점까지의 최단 경로를 찾기
- 파란 부분은 모른다고 했을 때, 현재 상태에서 가장 좋은 선택은 b를 선택하는 것이다.
- 그러나 결론적으로 최단 경로가 아니다!
-> Greedy Algorithm 으로 풀 수 있는 문제가 아니다.
2. Greedy Algorithm
탐욕적인 알고리즘이란
- 결정을 해야할 때마다 그 순간에 가장 좋다고 생각되는 것을 선택함으로써 최종적인 해답에 도달하기
- 그 순간의 선택은 local 최적이다. 이 선택을 모아만든 global 해답이 최적은 아닐 수 있기 때문에, 최적의 해답을 주는지 검증하는 과정이 필요하다.
- 현재 상태에서 최고를 고른 후 다음 단계로 가서 최고를 고르는 것을 반복하는 과정 (다시 돌아오는 일이 없어야 한다)
탐욕적인 알고리즘 설계 절차
- 선정과정 (selection procedure)
- 적정성점검 (feasibility check)
- 해답점검 (solution check)
2-1. 거스름돈 문제
- 동전의 개수가 최소가 되도록 거스름돈을 주는 문제
- 탐욕적인 알고리즘으로 풀기
- 거스름돈이 x일 때 가치가 가장 높은 동전부터 x를 초과하지 않도록 내준다
-> 우리나라의 동전으로 할 경우 최적의 해가 나온다.
- if) 12원 짜리 동전을 새로 발행한 경우 최적의 해가 아니다.
ex) 16원
-> 12∗1+1∗4=16 => 5개
-> 10∗1+5∗1+1∗1=16 => 4개
2-2. 그래프
그래프 intro
- 비 방향성 그래프 : G=(V,E)
- V는 정점, E는 이음선
- () 괄호를 쓰는 이유는 순서가 중요하기 때문이다.
2-3. 신장 트리 (spanning tree)
- 정의
- 연결된, 비방향성 그래프에서 순환 경로를 제거하면서 연결된 부분그래프가 되도록 이음선을 제거한 그래프
- 그래프 상에서 모든 노드가 사이클 없이 연결된 그래프 (트리)
- 신장트리의 개수
- t(G) : connected graph의 spanning tree개수
- 완전 그래프 (complete graph) : 모든 노드간에 에지가 존재하는 그래프
- 노드가 n개인 완전그래프의 edge개수는 nC2
- G가 완전그래프인 경우 t(G)=nn−2 (Cayley's formula)
- compelete biparite graph
- compelete biparite graph Kp,q인 경우 t(G)=pq−1qp−1
- biparite graph는 그룹간에는 edge가 존재하지만, 그룹 내에는 edge가 존재하지 않는 그래프
2-4. 최소비용 신장 트리 (minimum spanning tree)
- 신장트리가 되는 G의 부분그래프 중에서 가중치가 최소가 되는 부분그래프
무작정 알고리즘
- 모든 신장트리를 다 고려해보고, 최소 비용이 드는 것을 고르기
- 앞에서 말한 Cayley's formula에 의해 지수보다도 나쁜 알고리즘이 될 수 있다.
탐욕적인 알고리즘1 - Prim 알고리즘
- G=(V,E) 가 주어졌을 때 F⊆E를 만족하면서 (V,F)가 G의 MST가 되는 F 찾기
- 순서
- F=∅
- Y=v1
- while(사례 미해결)
3-1. 선정절차/적정성 점검 : V-Y에 속한 정점들 중에서 Y에 가장 가까운 정점 선정
3-2. 선정한 정점을 Y에 추가
3-3. Y로 이어지는 edge를 F에 추가
if(Y==V)
3-4. 해답 점검 : Y=V가 되면, T=(V,F)가 MST
- 쉽게 말하면..
- 처음에 한 노드를 선택하고 해당 노드를 제외한 다른 노드로 갈 수 있는 edge중에서 가중치가 가장 적은것 선택하기
- 선택한 다음 연결된 노드를 Y 집합에 넣고, V-Y (선택한 노드를 제외한 노드들)에서 처음에 실행한 방식을 반복해서 실행
- 모든 노드가 연결된 경우 끝
- feasibility test는 안한다. -> V-Y를 하는 과정에서 cycle가 생기는 것을 방지함
- pseudo code
W[i][j]=⎩⎪⎪⎨⎪⎪⎧edge 의 가중치inf0vi에서 vj로 가는 edge가 있는 경우vi에서 vj로 가는 edge가 없는 경우i=j 인 경우 - nearest[i] : Y에 속한 정점 중에서 vi에서 가장 가까운 정점의 인덱스
- distance[i] : vi와 nearest[i]를 잇는 이음선의 가중치
void prim(int n, const number W[][],set_of_edges& F)
{
index i, vnear; number min; edge e; index nearest[2..n]; number distance[2..n];
F = ϕ;
for(i=2; i <= n; i++)
{
nearest[i] = 1; // vi에서 가장 가까운 정점을 v1으로 초기화
distance[i] = W[1][i]; // vi과 v1을 잇는 edge의 가중치로 초기화
}
repeat(n-1 times)
{
min = ∞;
for(i=2; i <= n; i++)
if (0 <= distance[i] < min)
{
min = distance[i];
vnear = i;.
}
e = vnear와 nearest[vnear]를 잇는 edge;
e를 F에 추가;
distance[vnear] = -1;
for(i=2; i <= n; i++)
if (W[i][vnear] < distance[i]) // Y에 없는 노드들만 검색
{
distance[i] = W[i][vnear];
nearest[i]=vnear;
}
}
}
reapeat(n-1 times)if (W[i][vnear] < distance[i])
- 분석
- 위의 코드에서 repeat안에 for문이 따로 두 개 존재
T(n)=2(n−1)(n−1)∈Θ(n2)
탐욕적인 알고리즘2 - Kruskal 알고리즘
- F=∅
- 서로소가 되는 V의 부분집합들을 만드는데, 각 부분집합마다 하나의 정점만 가짐
- E (edge들의 set)안에 있는 edge들의 가중치를 비내림차순으로 정렬
- while(사례 미해결)
4-1. 선정절차 : 최소가중치를 갖고 있는 다음 edge를 선정
4-2. 적정성 점검 : 만약 선정된 edge가 두개의 서로소인 정점을 잇는다면, 먼저 그 부분집합을 하나의 집합으로 합치고, 다음에 edge를 F에 추가한다.
4-3. 해답점검 : 만약 모든 부분집합이 하나의 집합으로 합해지면 그 때 T=(V,F) 가 MST
- 쉽게 말하면...
- edge들을 가중치가 작은 순서대로 sorting 하여 가지고 있음
- 처음에는 모든 정점들이 각자 다른 set에 한 개씩 들어있음
- 전에 만든 sorting된 가중치를 작은 순서대로 시작해서 연결
- 연결된 두개의 정점은 하나의 set으로 통합
- 위의 과정을 반복 (이때 sorting된 가중치들을 선택할 때, 다른 set에 들어있는 정점의 연결인 경우만 연결시킨다.)
- Pseudo code
void kruskal(int n, int m, set_of_edges E, set_of_edges& F)
{
index i, j;
set_pointer p, q;
edge e;
E에 속한 m개의 이음선을 가중치의 비내림차순으로 정렬;
F = ϕ;
initial(n);
while (F에 속한 이음선의 개수가 n-1보다 작다)
{
e = 아직 점검하지 않은 최소의 가중치를 가진 이음선;
(i, j) = e를 이루는 양쪽 정점의 인덱스;
p = find(i);
q = find(j);
if (!equal(p,q))
{
merge(p,q);
e를 F에 추가;
}
}
}
while (F에 속한 이음선의 개수가 n-1보다 작다) !equal(p,q)
서로소 집합 추상 데이터타입
Ackermann 함수
- F(0)=1 F(i)=2F(i−1), for i>0
Kruskal 알고리즘의 분석
- n개의 vertex, m개의 edge
- edge 정렬 -> Θ(mlg m)
- initial(n) -> Θ(n)
- while문 -> 최대 m번 수행 Θ(mlg n)
=> 결론적으로 Θ(mlg m) 이 지배한다.
- 최악의 경우 모든 vertex가 연결된 그래프인 경우 m=nC2에 의하여 m=2n(n−1)∈Θ(n2)
=> 결론 : W(m,n)∈Θ(mlg m)=Θ(n2lg n)
prim 과 kruskal의 알고리즘 비교
- prim : 모든 경우에 Θ(n2)
- Kruskal
- W(m,n)에서 Θ(n2lg n)
- sparse 한 경우 Θ(nlg n)
- dense 한 경우 Θ(n2lg n)
- 결론 : sparse한 그래프인 경우 Kruskal 이 효과적이고, dense한 경우 Prim 알고리즘이 더 효과적이다.

