Algorithm : Divide and Conquer

분할 정복(Divide and Conquer)

• 분할: 해결하기 쉽도록 문제를 여러 개의 작은 부분으로 나누는 것
• 정복: 나눈 작은 문제를 각각 해결한다.
• 통합: (필요한 경우에는) 해결된 해답을 모은다.

1. 이분 검색 (Binary Search)

재귀적 방식

• 찾으려는 데이터(data)가 배열의 중간의 항목과 같으면 찾음, 그렇지 않은 경우 아래의 과정 수행
• 분할: 배열을 반으로 나누어서 data가 중앙에 위치한 항목보다 작으면 왼 중앙을 기준으로 왼쪽의 배열 반쪽을 선택, 그렇지 않으면 중앙을 기준으로 오른쪽 배열 반쪽을 선택
• 정복: 반쪽 배열에서 data를 검색
• 통합: 필요하지 않음

재귀로 구현된 이분 검색 코드(python)

s = [1,2,4,6,7,9,10]
data = 10

def binarySearchRecursion(low,high):
    if low > high:
        return -1
    else:
        mid = (high+low)//2
        if(data == s[mid]):
            return mid
        elif(data < s[mid]):
            high = mid -1
        else:
            low = mid+1
    return binarySearchRecursion(low,high)

참고) 재귀 알고리즘

• 재귀호출이 알고리즘의 마지막에 이루어 질 때를 tail recursion이라고 한다.
• 이러한 tail recursion은 iterative algorithm 으로 변환하기가 수월하다.
• 사실상 재귀라는 것은 사람이 편하기 위해서 만든 것이며, 모든 재귀는 반복문으로 변환할 수 있다.
• 재귀는 데이터를 stack에 저장해놓기 때문에 때에 따라 반복문보다 매우 느리게 동작할 수도 있다.

재귀를 쓰지 않은 이분 검색 코드(python)

s = [1,2,4,6,7,9,10]
data = 10

def binarySearchNonRecursion(low, high):
    while(low <= high):
        mid = (low + high)//2
        if(data == s[mid]):
            return mid
        elif(data > s[mid]):
            low = mid+1  
        else:
            high = mid-1
    return -1

최악의 경우 시간 복잡도 분석

• 경우 1) 반쪽 배열의 크기가 n/2일때
  $W(n) = W(n/2)+1$
  $n>1$이고, $n=2^k$ $(k\ge1), W(1) =1$
  반복 대입법을 통해
  $W(n) = W(n/2) + 1$
  $=(W(n/2^2)+1)+1$
  $=W(n/2^2)+2$
  ...
  $=W(n/2^k)+ k$
  $=1+k$
  $=log_2(n)+1$

• 경우 2) 일반적인 경우 - 반쪽 배열의 크기는 $\lfloor n/2 \rfloor$개
  (아래에서 $lg$는 밑이 2인 로그)
  $W(n) = 1+W(\lfloor n/2 \rfloor)$
  위에서 구한 결과를 바탕으로 $W(n) = \lfloor logn \rfloor +1$ 임을 수학적 귀납법으로 증명
  귀납 출발 : $n=1$이면 $W(1)=\lfloor log1 \rfloor+1 = 0+1=1$
  귀납 가정 : $n>1$이고, $1<k<n$인 모든 $k$에 대해서 , $W(k) =\lfloor logk \rfloor +1$이 성립한다고 가정
  귀납 단계
  1) n이 짝수이면
  $W(n) = 1+W(\lfloor n/2\rfloor)$
  $=1+ \lfloor lg\lfloor n/2\rfloor \rfloor+1$ -> 귀납가정에 의해서
  $=2+\lfloor lg\lfloor n/2\rfloor \rfloor$
  $=2+\lfloor lg(n/2) \rfloor$ -> n이 짝수이므로
  $=2+\lfloor lgn-1 \rfloor$
  $=1+\lfloor lgn \rfloor$
  2) n이 홀수이면 $\lfloor n/2 \rfloor = (n-1)/2$ 로 증명
  3) 따라서 $W(n) = \lfloor lgn \rfloor +1∈Θ(lgn)$

2. 합병 정렬 (Merge Sort)

• 분할 : 배열을 반으로 나눈다.
• 정복 : 나눠진 배열을 정렬한다.
• 통합 : 정렬된 배열들을 하나의 배열로 다시 통합한다.

재귀를 사용한 합병 정렬 코드(python) - 공간복잡도 O(2n)

def merge_sort(n, s):
    if n == 1:
        return
    
    h = n // 2
    m = n - h
    u = s[:h]
    v = s[h:]

    merge_sort(h, u)
    merge_sort(m, v)
    merge(h, m, u, v, s)

def merge(h, m, u, v, s):
    i = j = k = 0

    while i < h and j < m:
        if u[i] < v[j]:
            s[k] = u[i]
            i += 1
        else:
            s[k] = v[j]
            j += 1
        k += 1

    if i == h:
        while j < m:
            s[k] = v[j]
            j += 1
            k += 1
    else:
        while i < h:
            s[k] = u[i]
            i += 1
            k += 1

재귀를 사용하지 않은 합병 정렬 코드(python)

최악의 경우 시간 복잡도 분석

• 시간 복잡도 분석
  $W(h,m) = W(h)+W(m)+h+m-1$
  $W(h)$는 $V$를 정렬하는데 걸리는 시간 $W(m)$은 $U$를 정렬하는데 걸리는 시간, $h+m-1$은 합병하는데 걸리는 시간
  재현식은 $W(n) = 2W(n/2)+n-1$ 이고 조건은 $n>1, n=2^k(k\ge1), W(1)=1$ 이다.
  도사정리 2번을 적용하면 $W(n)∈Θ(nlgn)$

• 증명
  $W(n) = 2W(n/2)+n-1$ for $n\ge2$ with $W(1)=0, n=2^k$
  $W(n) = 2W(n/2)+n-1$
  $=2(2W(n/2^2)+n/2-1)+(n-1) = 2^2W(n/2^2)+(n-2)+(n-1)$
  $=2^2(2W(n/2^3)+n/2^2-1)+(n-2)+(n-1) = 2^3W(n/2^3)+(n-2^2)+(n-2)+(n-1)$
  $=2^kW(n/2^k)+(n-2^{k-1})+(n-2^{k-2}+...+(n-2)+(n-1)$
  $=kn-(1+2+2^2+...+2^{k-2}+2^{k-1})$
  ...
  $=nlgn-(n-1)$

공간복잡도 분석

• 제자리 정렬 알고리즘(in-place-sort): 추가적인 저장장소를 사용하지 않고 정렬하는 알고리즘
• 합병 정렬은 제자리 정렬 알고리즘이 될 수 없다.
• 위에서 언급한 재귀를 사용한 합병정렬 코드는 공간 복잡도가 O(2n)인 알고리즘이다.
  
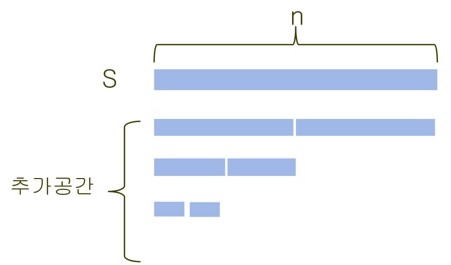
  • 위의 코드에서 mergeSort() 함수를 수행함에 따라 새로운 추가공간인 U 와V를 할당하게 된다.
  • 처음 배열의 크기가 n이라면, 첫 재귀 호출에서 n개 다음호출에서 n/2, n/4 ... 이므로 등차수열의 합을 통해 2n임을 구할 수 있다. ($2n∈Θ(n)$)
  • 해당 방식을 개선하여 mergeSort()함수에서 복사하는 내용을 없애면, O(n)인 알고리즘으로 만들 수 있다.

공간복잡도 개선된 합병 정렬 코드 - 공간 복잡도 O(n)

• 해당 코드에서는 U라는 합병할 때 사용하는 하나의 배열을 만들고 시작하기 때문에 U의 크기인 n만큼의 공간만 차지하면 하위 합병 과정에서는 U를 사용하여 공간 복잡도가 O(n)이 된다.

def mergeSort2(s, low, high): #데이터를 copy 하는 과정이 없다.
    mid = 0
    if(low < high):
        mid = (low+high)//2
        mergeSort2(s,low,mid)
        mergeSort2(s,mid+1, high)
        merge2(s,low,mid,high)

def merge2(s, low, mid, high):
    i = low
    j = mid + 1
    k = 0
    U = s[low:high+1] #합병시 사용하는 하나의 배열만 존재

    while i <= mid and j <= high:
        if s[i] < s[j]:
            U[k] = s[i]
            i += 1
        else:
            U[k] = s[j]
            j += 1
        k += 1
    while i <= mid:
        U[k] = s[i]
        k += 1
        i += 1
    while j <= high:
        U[k] = s[j]
        k += 1
        j += 1

    idx = 0
    while low <= high:
        s[low] = U[idx]
        low += 1
        idx += 1

3. 빠른 정렬 (Quick Sort)

특징

• not stable : 데이터가 동일한 key 인 경우에 정렬하고 나서 원래 순서가 달라지는 경우
• 실제로 절대적으로 빨라서 빠른 정렬 알고리즘은 아니다. 분할교환정렬(partition exchange sort)이 더 맞는 용어

빠른 정렬 코드 (python)

def quickSort(s,low,high):
    if(high>low):
        pivotPoint = partition(s,low,high)
        quickSort(s,low,pivotPoint-1)
        quickSort(s,pivotPoint+1,high)

def partition(s,low,high):
    pivotItem = s[low]
    j=low
    for i in range(low+1, high+1):
        if(s[i] < pivotItem):
            j+=1
            temp = s[j]
            s[j] = s[i]
            s[i] = temp
    pivotPoint = j
    temp = s[pivotPoint]
    s[pivotPoint] = s[low]
    s[low] = temp

    return pivotPoint

s=[3,5,2,9,10,14,4,8]
quickSort(s,0,7)
print(s)

최악의 경우 시간 복잡도 분석

• 입력이 비내림차순으로 정렬되어있는 경우
• partition 알고리즘에서 첫번째 항목만 제외하고 모든 항목을 비교하기 때문에 $T(n) = n-1$
• 재현식은 : $T(n) = T(n-1) + n-1, n> 0, T(0) = 0$
• 재현식을 풀면
  $T(n) = T(n-1) + n-1$
  $T(n-1) = T(n-2) + n-2$ -> $T(n) = T(n-2) +n-2 + n-1$
  -> $T(n) = 1+2+ ... +(n-1)$
  -> $T(n) = n(n-1)/2 ∈Θ(n^2)$

평균의 경우를 고려한 시간 복잡도 분석

• A(n)이 n개의 데이터를 정렬하는데 걸리는 평균 시간
• pivot item이 p번째 데이터가 될 확률 1/n, 기준점이 p일때 두 부분배열을 정렬하는데 걸리는 평균시간은 [A(p-1) + A(n-p)], 분할하는데 걸리는 시간은 n-1
• 평균적인 시간 복잡도는 $A(n) = \textstyle\sum_{p=1}^{n}{1/n[A(p-1) + A(n-p)]+n-1}$
• = $1/n[(A(0) + A(n-1)) +(A(1)+A(n-2))+...+(A(n-1)+A(0)] + n-1$
• = $2/n\sum_{p=1}^{n}A(p-1) + n-1$
• 양변에 n을 곱하고 n 대신 n-1 대입
• 정리하면 $A(n)/n+1 = A(n-1)/n + 2(n-1)/n(n+1)$
• $a_n = A(n)/n+1$
• 결과적으로 $a_n = \sum_{i=1}^{n} \frac{2(i-1)}{i(i+1)}$
• = $2(\sum_{i=1}^{n}\frac{1}{i+1}-\sum_{i=1}^{n}\frac{1}{i(i+1)})$
• 위의 식에서 우변은 매우 작으므로 무시
• 좌변을 근사하면 ln$(n)$ => $a_n =$ 2ln$(n)$
• 결론적으로 $A(n) = (n+1) a_n$ = $(n+1)2ln(n)$ = $(n+1)2(ln2)(lg(n)) ∈Θ(nlgn)$
• quick sort는 평균적으로 $O(nlgn)$의 알고리즘

4. 행렬 곱셈

단순한 행렬곱셈 알고리즘

• 시간복잡도를 계산하면 : n x n 행렬의 곱셈 -> $T(n) = n*n*n = n^3 ∈Θ(n^3)$
• 총 8번의 곱셈과 4번의 덧셈 필요 -> $T(n) = 8T(\frac{n}{2}), T(1) =1$

쉬트라센 방법

• n x n 행렬에서(n은 짝수) 각 행렬을 4개의 부분행렬로 나누고 계산하는 방식
• 곱셈과 덧셈을 나눠서 $m_1,m_2,...m_7$ 까지 나타냄
• 7번의 곱셈과 18번의 덧셈/뺄셈 필요
• 행렬의 크기가 커질수록 효율적인 방법
• $T(n) = 7T(\frac{n}{2}), T(1) = 1$
• 위의 식을 전개하면 $T(n)∈Θ(n^{2.81})$

5. 큰 정수 계산법

단순 곱셈

• 단순곱셈의 경우 $n^2$시간 걸림, 덧셈은 1차 시간에 완료 가능

방법 1

• n이 큰 정수의 숫자의 개수, $m = \lfloor n/2 \rfloor$
• ex) $9,423,723 = 9432 * 10^3 + 723 -> u = x*10^m + y$
  $u = x*10^m + y, v = w*10^m+z$ 라고 하면, $u*v = xw * 10^{2m} + (xz+ wy) * 10^m + yz$
• 결과적으로 $\frac{n}{2}$ 자리곱셈 4번(xw, xz, wy, yz) 으로 바뀜

방법 1의 최악의 경우 시간복잡도 분석

• $W(n) = 4W(\frac{n}{2})+cn, n>s$이고 n이 2의 거듭제곱 형태
• 재현식을 풀면 $W(n)∈Θ(n^{lg4})=Θ(n^{2})$
• 결론적으로 단순 곱셈 보다 빨라지지 않음

방법 2 (방법 1의 개선된 형태)

• 이전의 방법 1 에서는 $xw, xz+yw, yz$의 계산이 필요
• $r$ 이라는 계산을 추가
• $r = (x+y) * (w+z) = xw + (xz+yw)+yz$ -> 곱셈 한번
• $xz + yw = r-xw-yz$ -> 곱셈 두번
• 결론적으로 곱셈의 수를 한번 줄일 수 있음

큰 정수 계산법 방법 2 코드(python)

import math

def prod2(u,v):
    n = max(len(str(u)), len(str(v)))
    if(u == 0 or v == 0):
        return 0
    elif (n <= 4):
        return u*v
    else:
        m = math.floor(n/2)
        x = u // 10**m
        y = u % 10**m
        w = v // 10**m
        z = v % 10**m
        r = prod2(x+y, w+z)
        p = prod2(x,w)
        q = prod2(y,z)
        return p*10**(2*m) + (r-p-q)*(10**m) + q

방법 2의 최악의 경우 시간복잡도 분석

• prod2(x+y, w+Z), prod2(x,w), prod2(y,z)
• 위의 세 번의 연산을 해야하기 때문에 $3W(\frac{n}{2}) + cn \le W(n) \le 3W(\frac{n}{2} + 1) + cn , W(s)=0$
• $W(n)∈Θ(n^{lg3})∈Θ(n^{1.58})$

6. 임계값 결정

• divide and conquer 방법에서 큰 문제를 어느 크기의 문제가 될 때까지 분할할 것인가
• 합병정렬과 교환정렬 중 어떤 임계값에서 어떤 정렬을 선택해야 하는가..
• merge sort2의 경우
  • 분할하고 재합병하는데 걸리는 시간 $32n \mu s$ 으로 가정
  • $W(n) = W(\lfloor(\frac{n}{2})\rfloor +W(\lceil(\frac{n}{2})\rceil) + 32n\mu s, W(1) = 0\mu s$
  • 단순화 시키면, $W(n) = 2W(\frac{n}{2}) + 32n\mu s$, n>1, n은 2의 거듭제곱
  • => $W(n) = 32nlgn \mu s$
• 교환정렬의 경우
  • $\frac{n(n-1)}{2} \mu s$
• 그렇다면 어느 지점에서 합병정렬에서 교환정렬로 바꿔 계산하는 것이 빠른가
  • $\frac{n(n-1)}{2} \mu s < 32nlgn \mu s$ 를 만족하는 n ?
  • n < 591의 결과가 나온다. 그러나 이 경우, $32nlgn$은 문제 크기가 1이 될 때 까지 분할한 경우의 복잡도 이므로 틀린 분석
• 정확한 분석
  • 합병정렬에서 교환정렬로 넘어가는 그 지점을 찾아야 한다!
  • $W(n)= \begin{cases} \frac{n(n-1)}{2} \mu s, & {n\le t} \\ W(\lfloor(\frac{n}{2})\rfloor +W(\lceil(\frac{n}{2})\rceil) + 32n\mu s, & n>t \end{cases}$
  • $\frac{t(t-1)}{2} = W(\lfloor(\frac{t}{2})\rfloor +W(\lceil(\frac{t}{2})\rceil) + 32t$ 를 풀면 t가 짝수인 경우 t=128, 홀수인 경우 t = 128.008 이 정확한 threshold 이다.

7. 분할 정복을 사용하지 말아야 하는 경우

• 크기가 n인 입력이 2개 이상의 조각으로 분해되며, 분할된 부분의 크기가 거의 n에 가깝게 되는 경우 -> 시간 복잡도가 지수 시간인 경우
  • ex) $T(n) = 2T(n-1) + n$
• 크기가 n인 입력이 거의 n개 이상의 조각으로 분해되며, 분할된 부분의 크기가 n/c인 경우(c는 상수) -> 시간 복잡도 $Θ(n^{lgn})$
  • ex) $T(n) = nT(n/2) + n$

8. 도사 정리

공식

• $T(n) = aT(\frac{n}{b}) + cn^k$, (n>1이고, n이 b의 거듭제곱)
• $T(1) = d$
• $T(n) ∈ \begin{cases} Θ(n^{k}), & {if (a<b^k)} \\ Θ(n^{k}lgn), &{if (a=b^k)} \\ Θ(n^{log_ba}), &{if (a>b^k)} \end{cases}$

예시

$T(n) = T(\frac{n}{2}) + 1$ 인 경우
-> $a = 1, b = 2, c = 1, k = 0$
-> 공식 2번째 case에 해당한다
-> 결론 : $Θ(lgn)$