Neural Collaborative Filtering

ETER2·2023년 2월 13일

Collaborative Filtering Deep Learning Implicit feedback Matrix Factorization Neural Networks

ABSTRACT

해당 연구에서는 추천 시스템의 가장 큰 문제인 collaborative filtering을 해결하려고 하였다. collaborative filtering은 유저와 항목 기능 간 상호작용을 모델링할 때, 행렬 분해(matrix fatorization)에 의존하고 유저와 항목의 잠재 기능에 내적을 적용한다. 이 내적을 데이터에서 임의의 함수를 학습할 수 있는 뉴럴 구조로 대체한, NCF(Neural network based Collaborative Filtering)라는 프레임워크를 제시하였다. NCF는 포괄적이고, 일반적인 행렬 분해를 표현할 수 있다고 하였다.

INTRODUCTION

개인화 된 추천 시스템의 핵심은 과거 상호작용을 기반으로 항목에 대한 사용자의 선호도를 모델링하는 것이다(collabrative filtering). 다양한 collabrative filtering 기술 중 유저와 항목을 잠재적 특징의 벡터를 사용하여 공유 잠재 공간에 투영하여 유저나 항목을 표현하는 matrix factorization(MF)가 가장 인기있다. 이후 유저의 상호작용은 잠재 벡터의 내적으로 모델링된다. MF를 향상시키기 위한 후속 연구와 MF의 효과에도 불구하고, 상호작용 함수인 내적으로 인해 성능이 저해된다는 것은 잘 알려져 있다. 이 논문에서는 데이터에서 interaction function을 학습하기 위해 deep neural network(DNN)의 사용을 탐구한다. MF 방법에 DNN을 적용한 연구는 상대적으로 적다. DNN을 추천 시스템에 적용하더라도 여전히 MF에 의존하며, 내적을 사용해 유저와 항목의 잠재 기능을 결합한다.
본 연구는 신경망 모델링 접근법을 공식화하여 문제를 해결한다. 사용자의 행동을 통해 간접적으로 사용자의 선호도를 반영하는 implicit feedback에 중점을 둔다. implicit feedback은 사용자 만족도가 관찰되지 않고, 부정적 피드백이 부족하기 때문에 활용하기가 어렵다. 본 논문에서는 DNN을 활용해 노이즈가 많은 implicit feedback 신호를 모델링하는 방법을 탐구한다.

contribution

사용자와 항목의 잠재적 특징을 모델링하기 위한 신경망 구조를 제시하고, 신경망을 기반으로 collaborative filtering을 위한 NCF를 고안한다.
MF는 NCF의 한 종류가 될 수 있고, 다층 퍼셉트론을 활용하여 높은 수준의 비선형성을 부여할 수 있음을 보여준다.
NCF의 효과와 collaborative filtering을 위한 딥 러닝의 가능성을 입증한다.

PRELIMINARIES

Learning from Implicit Data

y_{ui}= \begin{cases} 1,\;if\;interaction\;(user\;u,\;item\;i)\;is\;observed;\\ 0,\;otherwise. \end{cases}

user u와 item i의 상호작용이 있을 경우 1, 없을 경우 0. $y_{ui}$ 가 1이라는 것은 상호작용이 존재한다는 것이지 사용자가 해당 항목을 선호한다는 것이 아니다. 동일하게 $y_{ui}$ 가 0이라는 것은 상호작용이 존재하지 않는다는 것이지 사용자가 해당 항목을 비선호한다는 의미가 아니다. 사용자가 항목을 인식하지 못하는 경우도 포함된다. 따라서 관찰되지 않은 항목을 추정하는 문제가 된다.

\hat{y}_{ui} = f(u,i|\Theta)

$\hat{y}_{ui}$ 는 상호작용의 예측 점수 $\Theta$ 는 모델 파라미터를, $f$ 는 모델 매개변수를 예측 점수에 매핑하는 함수이다. $\Theta$ 를 추정하기 위해 일반적으로 목적 함수를 최적화하는 기계 학습 패러다임을 따른다. 두 가지 유형의 목적 함수가 있는데 pointwise loss와 pairwise loss이다. pointwise의 경우 $\hat{y}_{ui}$ 과 $y_{ui}$ 의 차이(squared loss)를 최소화하며 regression 문제에 주로 사용된다. 관찰되지 않은 항목을 부정적인 피드백으로 처리하거나, 샘플링하였다. pairwise learning은 관찰된 항목의 순위가 관찰되지 않은 항목보다 높아야 한다는 아이디어를 기반으로 하였다. 예측값과 실제값의 손실을 최소화하는 대신 관측값과 관츨되지 않은 값의 margin을 최대화 한다. NCF는 신경망을 사용하여 상호작용 함수를 매개 변수화하기 때문에 pointwise와 pairwise learning을 전부 사용한다.

Matrix Factorization

MF는 사용자와 항목을 잠재적 특징의 실제 벡터와 연결한다. $p_u$ 와 $q_i$ 를 user u와 item i의 잠재 벡터라고 할 때, MF는 $y_{ui}$ 의 추정을 $p_u$ 와 $q_i$ 의 내적으로 한다.

\hat{y}_{ui} = f(u,i|p_u, q_i) = p_u^Tq_i = \sum_{k=1}^K{p_{uk}q_{ik}}

K는 잠재 공간의 차원을 나타낸다. MF는 사용자와 항목의 양방향 상호작용을 모델링한다. 잠재 공간의 각 차원이 독립적이고 동일한 가중치로 선형 결합한다고 가정한다. 따라서 MF는 잠재 요인의 선형 모델로 간주된다.

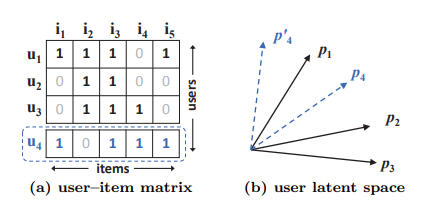
내적 함수와 MF의 한계를 나타낸 그림이다. 자카드 계수를 사용하여 유사도를 측정한 결과 (a)에서는 $s_{23}(0.66) > s_{12}(0.5) > s_{13}(0.4)$ 의 결과가 나오고 따라서 (b)와 같이 $p_1, p_2, p_3$ 의 기하학적 관계가 표현된다. 새로운 유저 $u_4$ 를 고려한다고 할 때, 해당 유저의 입력은 (a)의 점선으로 제공된다. 따라서 $s_{41}(0.6) > s_{43}(0.4) > s_{42}(0.2)$ 의 결과를 얻을 수 있다. 이는 $u_4$ 가 $u_1$ 과 가장 유사하고 $u_3$ , $u_2$ 순서임을 의미한다. MF 모델이 (b)에서 $p_4$ 를 $p_1$ 과 가장 가깝게 배치 할 경우, 두 가지 옵션 중 어떤 위치에 배치하더라도 $p_2$ 가 $p_3$ 보다 가깝다.

저차원 잠재 공간에서 사용자와 항목 간 복잡한 상호작용을 추정하는 데 단순하고 고정된 내적을 사용하면서 발생한 문제이고 MF의 한계를 보여준다. 이 문제를 해결하기 위해 잠재적 요소 K를 사용할 수 있지만 (축을 하나 더 추가), 모델의 일반화에 악영향을 미칠 수 있다. 따라서 본 연구에서는 DNN을 사용하여 데이터 사이의 상호작용을 학습시켜 한계를 해결한다.

NEURAL COLLABORATIVE FILTERING

General Framework

collaborative filtering에서 full neural treatment를 허용하기 위해 multi-layer representation을 채택하여 사용자-항목 상호작용 $y_{ui}$ 를 모델링한다. 출력 레이어는 다음 레이어의 입력 역할을 한다. 하단 입력 레이어는 user u와 item i를 설명하는 두가지 특징 벡터 $V_u^U$ 와 $V_i^I$ 로 구성된다.

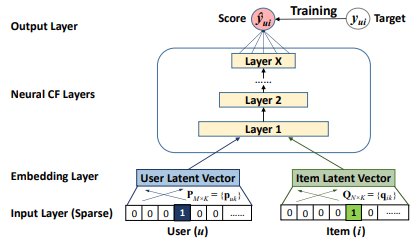
이 연구에서는 pure collaborative filtering 설정에 초점을 맞추고 있기 때문에 사용자와 항목의 one-hot encoding 벡터로 변환해 input으로 사용한다. input layer 위에는 embedding layer가 있는데 fully-connected layer를 사용해 sparse representation을 dense vector로 바꿔준다. 얻어진 사용자, 항목 임베딩은 잠재 벡터로 볼 수 있다. 이 임베딩은 multi-layer neural architecture (neural collaborative filtering layer)에 공급되어 잠재 벡터를 예측 점수로 매핑한다. neural CF layer의 각 layer는 사용자-항목 상호작용의 잠재 구조를 발견하도록 커스텀될 수 있다. 마지막 hidden layer X의 차원 따라 모델의 능력이 결정된다. Output layer는 예측 점수 $y_{ui}$ 이며, 예측값 $\hat{y}_{ui}$ 와 목표값 $y_{ui}$ 사이의 pointwise loss를 최소화하여 훈련을 수행한다.

\hat{y}_{ui} = f(P^Tv_u^U,Q^Tv_i^I|P,Q,\Theta_f)

NCF의 예측 모델을 위 식으로 공식화 할 수 있다. $P \in \mathbb{R}^{M \times K}$ 이고, $Q \in \mathbb{R}^{M \times K}$ (각 user latent factor matrix, item latent factor matrix)이다. $\Theta_f$ 는 상호작용 함수 $f$ 의 모델 파라미터이다. $f$ 를 multi-layer neural network로 정의했기 때문에 다음과 같이 표현할 수 있다.

f(P^Tv_u^U,Q^Tv_i^I)= \phi_{out}(\phi_X(...\phi_2(\phi_1(P^TV_u^U,Q^TV_i^I))...))

Learning NCF

pointwise 방법은 squared loss 함수를 주로 사용한다.

L_{sqr} = \sum_{(u,i) \in \mathcal{Y}\cup\mathcal{Y}^-}w_{ui}(y_{ui}-\hat{y}_{ui})^2

$\mathcal{Y}$ 는 $Y$ 의 관측된 상호작용의 집합이며 $\mathcal{Y}^-$ 는 negative instances, 관측되지 않은 상호작용의 집합이다. $w_{ui}$ 는 가중치를 나타내는 hyper parameter이다. 이 loss function은 데이터들이 가우시안 분포에서 왔다는 가정 하에 설정하는 squared loss이다. NCF는 사용자가 항목과 상호작용 했는지 여부를 binary 형태로 표현한 implicit data를 사용하기 때문에 잘 일치하지 않을 수 있다. 따라서 예측 점수 $\hat{y}_{ui}$ i가 u와 관련 있을 가능성을 나타낸다. 0과 1 범위의 확률을 부여하기 위해 output layer $\phi_{out}$ 의 활성화 함수로 probabilistic function을 사용한다. 따라서 다음과 같은 likelihood function을 사용한다.

p(\mathcal{Y},\mathcal{Y}^-|P, Q,\Theta_f)= \prod_{(u,i)\in\mathcal{Y}}\hat{y}_{ui}\prod_{(u,j)\in\mathcal{Y}}(1-\hat{y}_{uj})

negative logarithm likelihood는 다음과 같다. (loss function이 binary cross entropy loss와 동일)

L= -\sum_{(u,i) \in \mathcal{Y}}log\;\hat{y}_{ui}-\sum_{(u,j) \in \mathcal{Y}}log\;(1-\hat{y}_{uj})

이는 NCF 방법을 최소화하기 위한 목적 함수이며, SGD를 사용하여 최적화한다.

Generalized Matrix Factorization (GMF)

input layer에서 user와 item의 원 핫 인코딩을 진행하여 얻어진 임베딩 벡터를 latent vector로 볼 수 있다. 사용자 잠재 벡터 $P_u$ 를 $P^Tv_u^U$ 로, 항목 잠재 벡터 $q_i$ 를 $Q^Tv_i^I$ 로 볼 때, 첫 번째 neural CF layer의 매핑 함수를 다음과 같이 정의할 수 있다.

\phi_1(p_u,q_i)= p_u\odot q_i

$\odot$ 은 element-wise product of vector (성분곱)이다. 이 식을 output layer로 project하면 다음과 같은 식을 얻을 수 있다.

\hat{y}_{ui} = a_{out}(h^T(p_u \odot q_i))

$a_{out}$ 은 활성 함수, $h$ 는 output layer의 가중치를 나타낸다. $a_{out}$ 으로 identity function을 사용하고, $h$ 가 1로 이루어진 uniform vector라면 MF와 동일한 형태가 된다.

sigmoid function인 $\sigma = 1/(1+e^{(-x)})$ 을 $a_{out}$ 함수로 사용하고 $h$ 를 log loss가 있는 data (uniform 하지 않은 vector)를 사용한 일반화 된 버전의 MF를 사용하는데, 이를 Generalized Matrix Factorization(GMF)라고 하였다.

Multi-Layer Perceptron (MLP)

NCF는 사용자와 항목 간 두 pathway를 채택하기 때문에 특징을 결합하는 것이 직관적이다. 그러나 단순한 벡터 연결만으로 collaborative filtering effect를 모델링하기 충분하지 않다. 표준 MLP를 사용하여 사용자와 항목, 잠재 기능 간 상호작용을 학습하여 연결 벡터에 hidden layer를 추가할 것을 제안한다. 이를 통해 flexibility와 non-linearity를 부여할 수 있다. MLP는 다음과 같이 정의된다.

z_1 = \phi_1(p_u,q_i)= \begin{bmatrix} p_u\\ q_i \end{bmatrix} \\ \phi_2(z_1)=a_2(W_2^Tz_1 + b_2),\\ ......\\ \phi_L(z_{L-1})=a_L(W_L^Tz_1+b_L),\\ \hat{y}_{ui}=\sigma(h^T\phi_L(z_{L-1})),

x번째 layer 퍼셉트론의 $W_x$ 는 가중치 행렬, $b_x$ 는 편향 벡터, $a_x$ 는 활성화 함수이다. MLP 레이어의 활성함수는 sigmod, tanh, ReLU를 자유롭게 선택할 수 있다.

Fusion of GMF and MLP

GMF와 MLP가 같은 임베딩 레이어를 공유하면 가장 쉽게 결합할 수 있지만, 동일한 사이즈를 가질 때만 사용할 수 있기 때문에 성능이 제한될 수 있다.

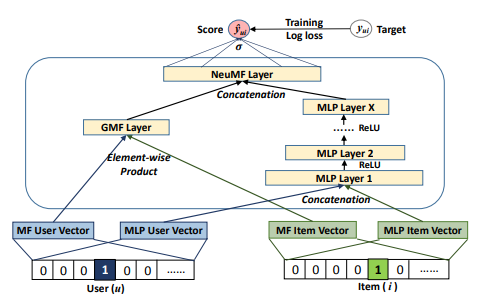
따라서 flexibility한 결합 모델을 제공하기 위해, 임베딩을 분리하고 마지막 hidden layer에서 두 모델을 결합한다.

\phi^{GMF}=p_u^G \odot q_i^G,\\ \phi^{MLP}=a_L(W_L^T(a_{L-1}(...a_2(W_2^T \begin{bmatrix} p_u^M\\ q_i^M \end{bmatrix} + b_2)...)) + b_L,\\ \hat{y}_{ui} = \sigma(h^T \begin{bmatrix} \phi^{GMF}\\ \phi^{MLP} \end{bmatrix})

이 모델을 Neural Matrix Factorization, 즉 NeuMF로 한다.

Pre-training

Pre-train 된 GMF와 MLP로 NeuMF를 초기화하는 것을 제안한다. GMF와 MLP를 수렴할 때까지 무작위로 초기화를 진행하고, NeuMF 매개 변수를 해당 모델의 파라미터를 사용 해 초기화한다. $\alpha$ 값을 이용해 두 모델의 가중치를 연결한다.

ETER2

이전 포스트

[TIL] C++ 기본 문법 (2)

다음 포스트