[논문] MotionDiffuse: Text-Driven Human Motion Generation with Diffusion Model
Motion Generation 논문 리뷰
지금은 LLM과 Diffusion Model이 모션 생성(Motion Generation) 분야에서 활발히 활용되고 있습니다. 이러한 연구들은 초기 모델들과 많이 비교되거나, 기존 모델을 기반으로 더 고도화된(advanced) 버전을 제시하는 경우가 많습니다.
또한, 새로운 연구에서는 이전 연구의 일부 내용을 생략하는 경우도 많죠. MotionDiffuse도 마찬가지입니다. Diffusion Model을 최초로 모션 생성에 적용한 모델이며, 이후 많은 연구에서 비교 기준이자 기반 기술로 활용되고 있습니다.
앞으로의 연구들을 더 잘 따라가고 이해하려면, 이렇게 기본이 되는 핵심 논문들을 확실히 짚고 넘어가는 것이 중요하겠죠? 😊
https://mingyuan-zhang.github.io/projects/MotionDiffuse.html
https://arxiv.org/abs/2208.15001
https://github.com/mingyuan-zhang/MotionDiffuse
Introduction
앞서 연구된 TEMOS와 MotionCLIP는 각각 스타일화를 하지 못하는 점과, 스타일화는 되어도 입력 텍스트의 길이가 한정되어 유저의 사용성에 있어 크게 제한되었다. 앞서 언급된 문제를 해결하기 위해, 저자들은 MotionDiffuse를 제안하였습니다. 구체적으로, DDPM과 달리 Cross-Modality Linear Transformer를 적용하여 생성되는 모션 길이 제한을 해결하였고, 더불어 모션의 다양성도 크게 증가되었다고 합니다. 또한, 신체 부위(상체와 하체)를 독립적으로 생성할 수 있도록 noise interpolation 기법을 제안했습니다. 더아가, auto-regressive방식이 긴 모션 시퀀스에 대한 학습을 필요로 하는 것과 달리, 새로운 샘플링 방식으로 추가학습 없이 동박간의 상관관계를 모델링 할 수 있도록 하였습니다.
- Main Contribution
- Probablistic Mapping: DDPM을 활용한 확률적 방식의 모션 생성
- Realistic Synthesis: 두가지 조건부 모션 생성에서 SOTA
- Multi-Level Manipulation: 전체적인 신체 동작을 제어하고, 시간에 따라 변화는 동작도 가능
Methodology
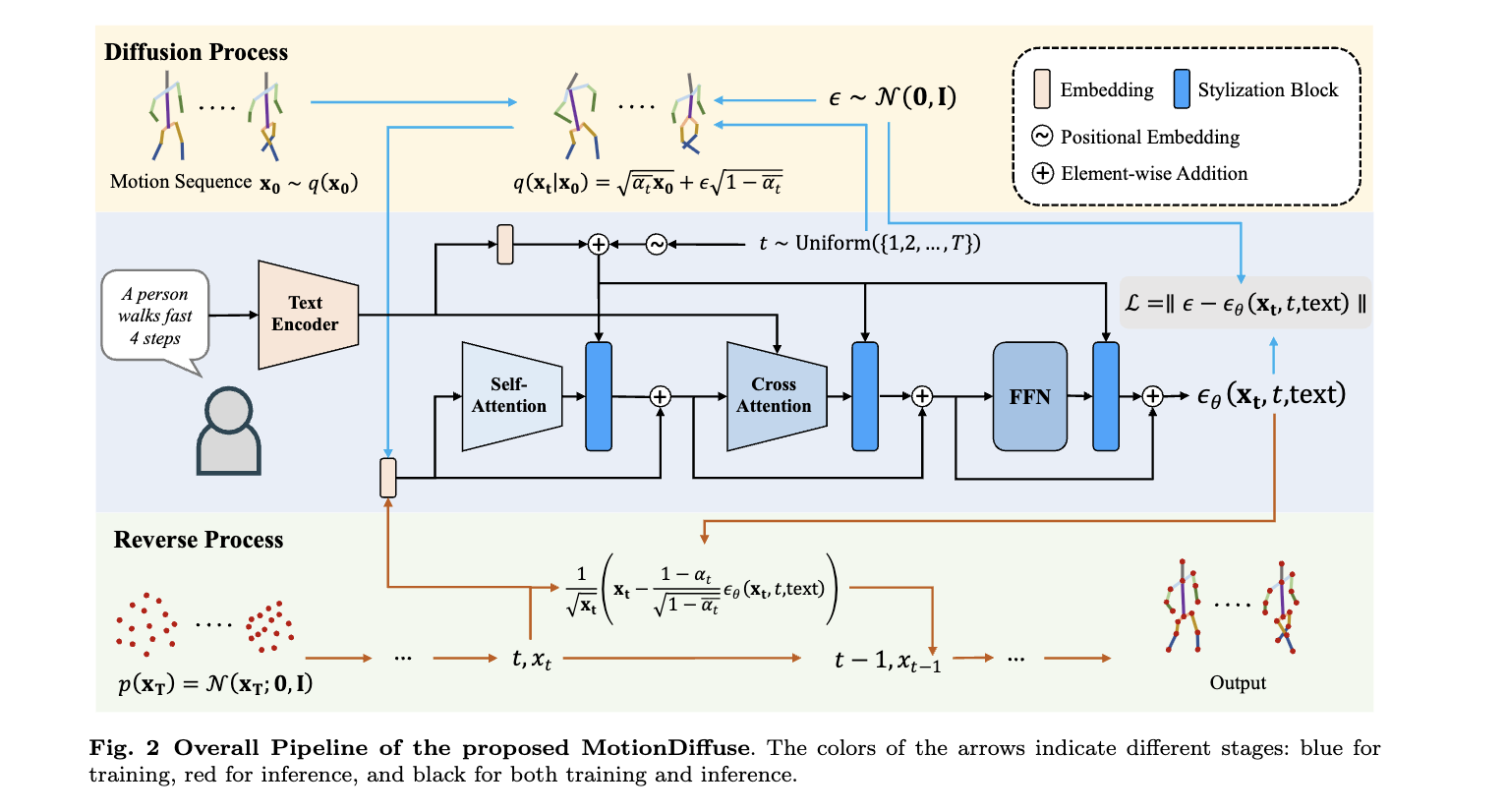
Pipeline Overview
- DDPM(Denoising Diffusion Probabilistic Model)을 사용한 text-conditioned motion generation
- denoising 과정에 Cross-Modality Linear Transformer 제안
- part-aware text controlling과 time-varied controlling
Diffusion Model for Motion Generation
- 가우시안 노이즈를 점진적으로 제거하며 모션을 생성하는 방식
- 학습 과정에서는 노이즈 을 예측하는 신경망을 훈련
- 샘플링 과정에서는 초기 노이즈에서 시작하여 점진적으로 원래 모션을 복원
- 최종적으로 text 조건으로 다양한 모션을 생성
Cross-Modality Linear Transformer
- 기존 UNet방식의 diffusion model은 convolution기반이라 가변 길이의 모션을 생성할 수 없기 때문에 Cross-Modality Linear Transformer사용.
- text encoder와 motion decoder로 구성
Text Encoder
- classical transformer
- 입력 데이터가 embedding layer를 거쳐 embedding feature를 출출되며 transformer block들에서 추가적으로 처리됨
- transformer blocks: Multi-Head Attention(MHA) 와 Feed-Forward Network(FFN)
- MHA의 입력: embedding feature을 몇개로 나눈
- MHA의 출력: Y = 들의 concatenation
- MHA 모듈의 입출력에는 residual connection 적용
- MHA 이후, 세 개의 linear transformations 과 두 개의 GELU로 구성된 FFN에서 처리
- 일반화 성능 강화를 위해 CLIP 모델의 weight를 사용하여 초기 몇개의 layer 학습. 그 이후 freeze.
Linear Self-attention
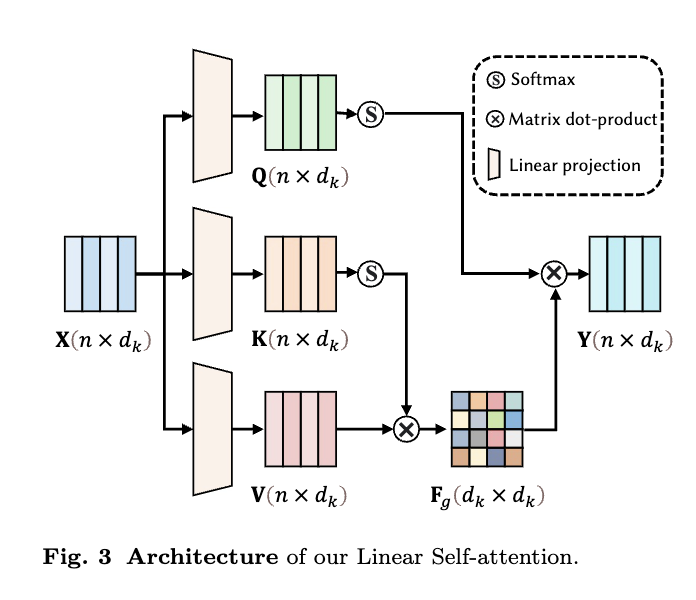
: 서로 다른 프레임간의 상관관계 모델링을 통한 모션 특징 강화
- self attention: 입력 시퀀스를 전체를 고려하며 노이즈를 보다 정확히 예측
- 단점: 시간 복잡도
- efficient attention: 프레임 간 쌍의 어텐션 가중치를 계산하는 대신, global feature map 생성. 는 multi-head의 split
- 장점
- 시간 복잡도:
- 더 global 정보 반영
Linear Cross-attention
- K와 V를 계산할 때, 입력 X대신 text feature사용.
Stylization Block
각 Linear Self-attention block, Linear Cross-attention block, and FFN block뒤에 추가되어 denoising timestamp 정보 반영
- input: , 다른 블록에서 출력된 원본 특징
- output:
- :Hadamard product, 요소별 곱
- : non-linear transformation
- : linear projections
- : Positional Embedding사용, : linear transformation 사용
Fine-grained Controlling
: DDPM으로 생성된 모션 시퀀스는 lantent space에 압축된 형태가 아닌, 명시적인 형식으로 존재하기 때문에 다양한 조작이 가능
Body Part-independent Controlling
: 텍스트 설명이 부족하기 때문에, 텍스트 설명만으로 신체 부위별 정확한 모션 제어 불가능합니다. 상하체의 움직임이 분리된 프롬포트(‘a person is running and waving left hand’)는 모델에게 어려운 문제이죠. 그렇다고 단순히 둘을 나눠서 ‘a person is running’을 하체에게, ‘a person is waving left hand’을 상체에게 따로 배분하는 것도 결코 쉽지 않습니다.
이 문제를 직관적으로 해결하려면 두개의 모션 시퀀스를 개별적으로 생성한 후 결합하는방법입니다. 하지만 이 둘을 단순히 다시 합치는 것은 모션이 굉장히 부자연스러워질 수 있기 때문에, Noise Interpolation을 활용한 개선 방법을 제안하였습니다.
- 기존 노이즈 제거 과정에서 노이즈
- : 프레임 개수, : 관절의 회전과 이동에 관한 정보 차원 크기
- 신체 부위별 노이즈를 분할: : 신체 부분 개수
- 각 신체 부위에 따른 노이즈를 예측 후 binary mask를 사용하여 어떤 부위를 강조할지 선택 후 결합
- 하지만, 여전히 신체 부위 간의 부드러운 전환 부족
- Smooth interpolation: 보간을 부드럽게 만드는 corrextion term 추가
-
- : gradient calculation, : hyperparameter for smoothness.
-
Time-varied Controlling
- 주어진 입력 배열 : 동작 구간.
- 각 구간에 대한 노이즈 항:
- 목표 전체 시퀀스 길이
- 각 노이즈 항을 zero padding하여 로 확장
- 그 후, 노이즈 보간
- 효과: 연속적인 방식으로 다양한 동작을 포함하는 장기 모션을 생성 가능
Experiments
- Dataset: KIT-ML, HuamnML3D
- Metircs: FID, R-Precision, Diversity, MMdality, MM-Dist
- Implementation Details: 100K iter for HumanAct12 dataset and 500K iterations for the UESTC dataset, both with a 0.0001 learning rate.
Results
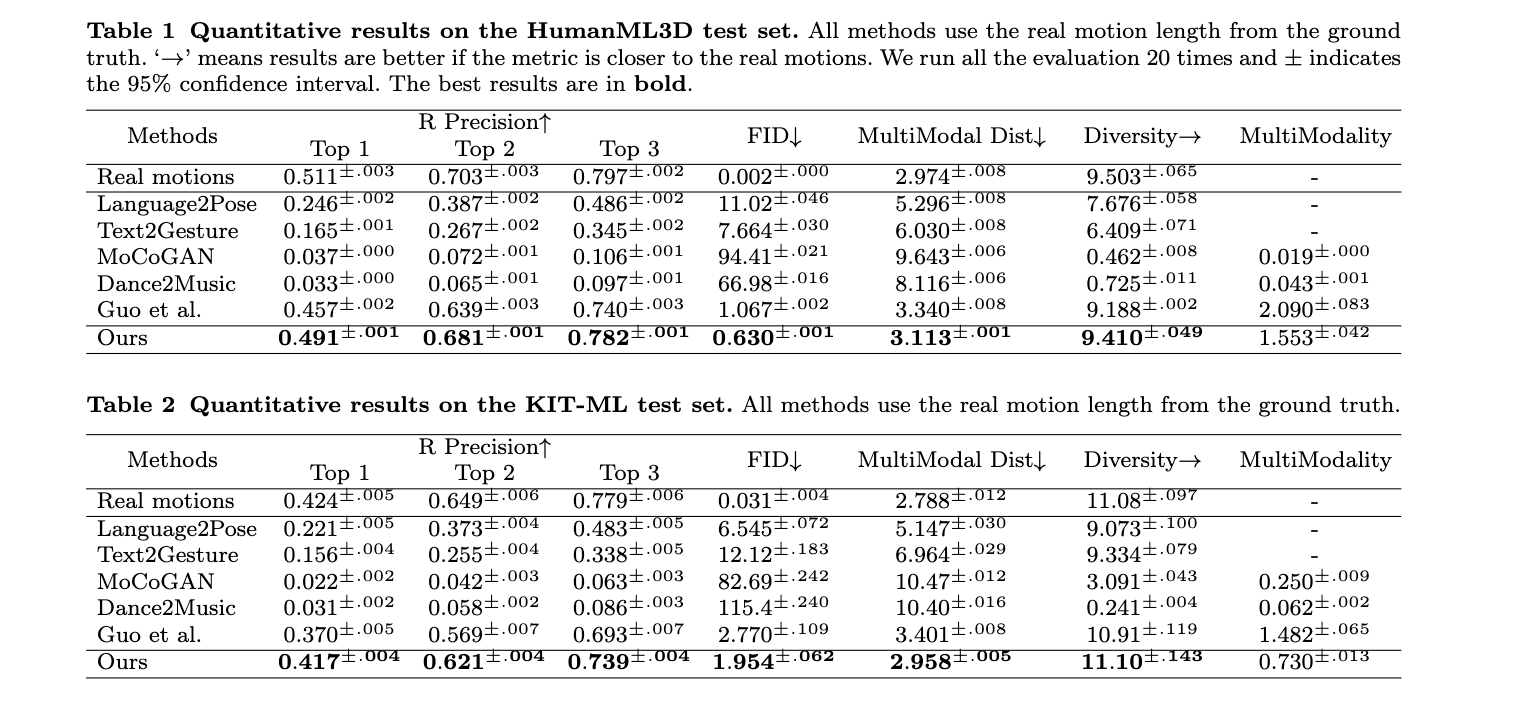
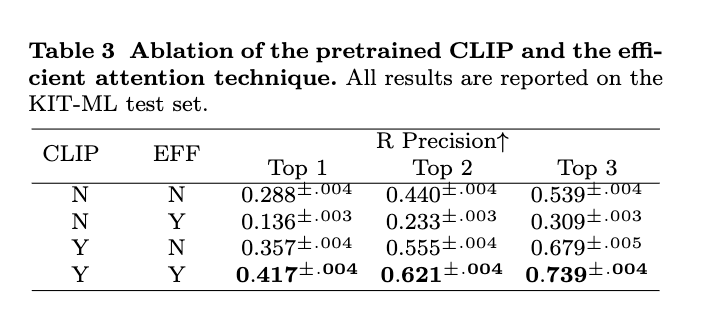
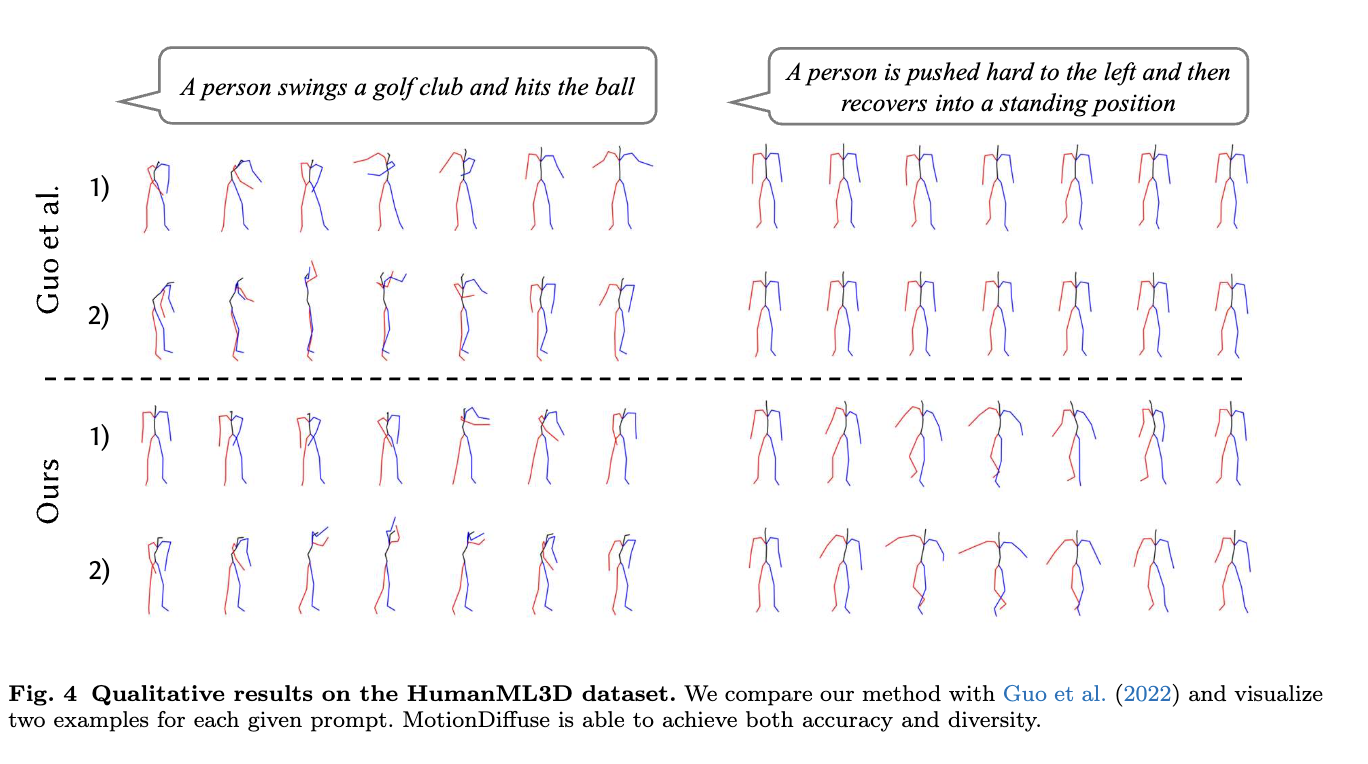
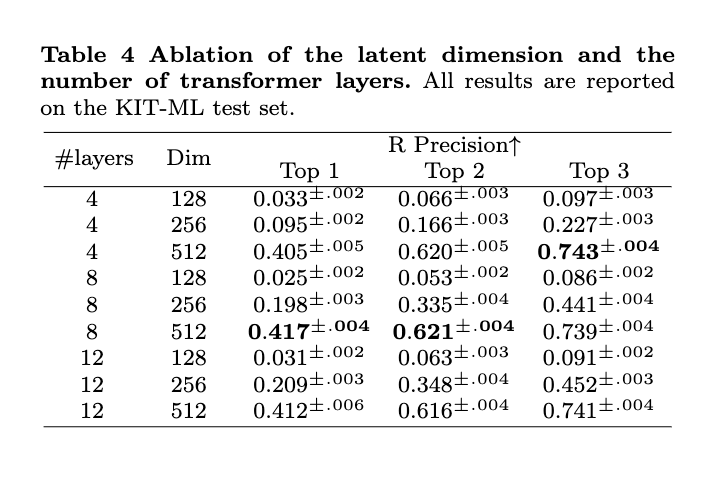
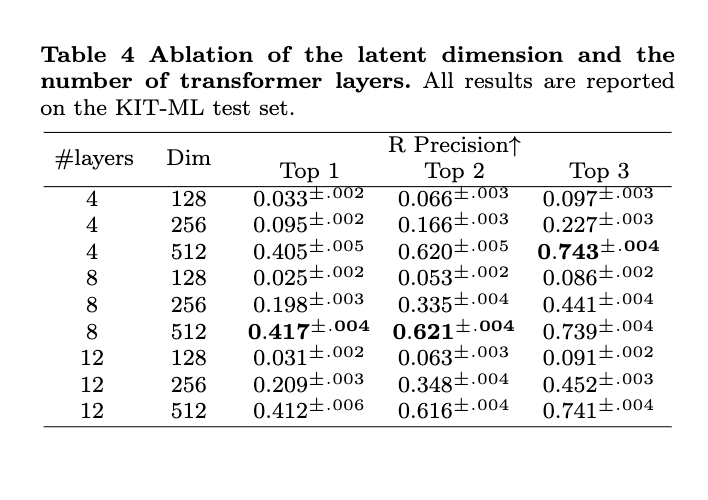
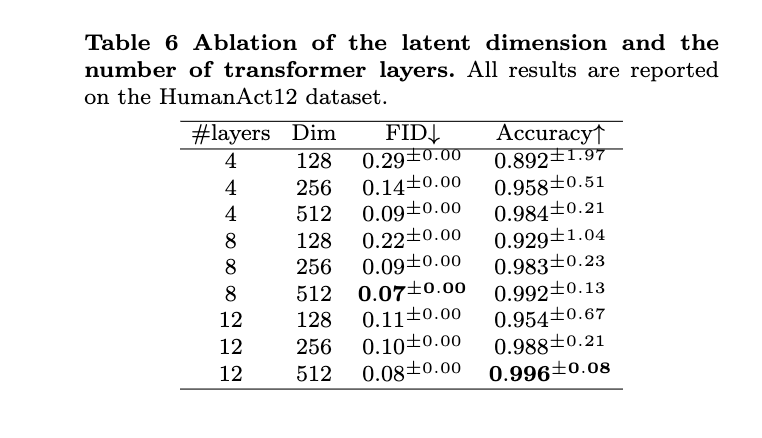
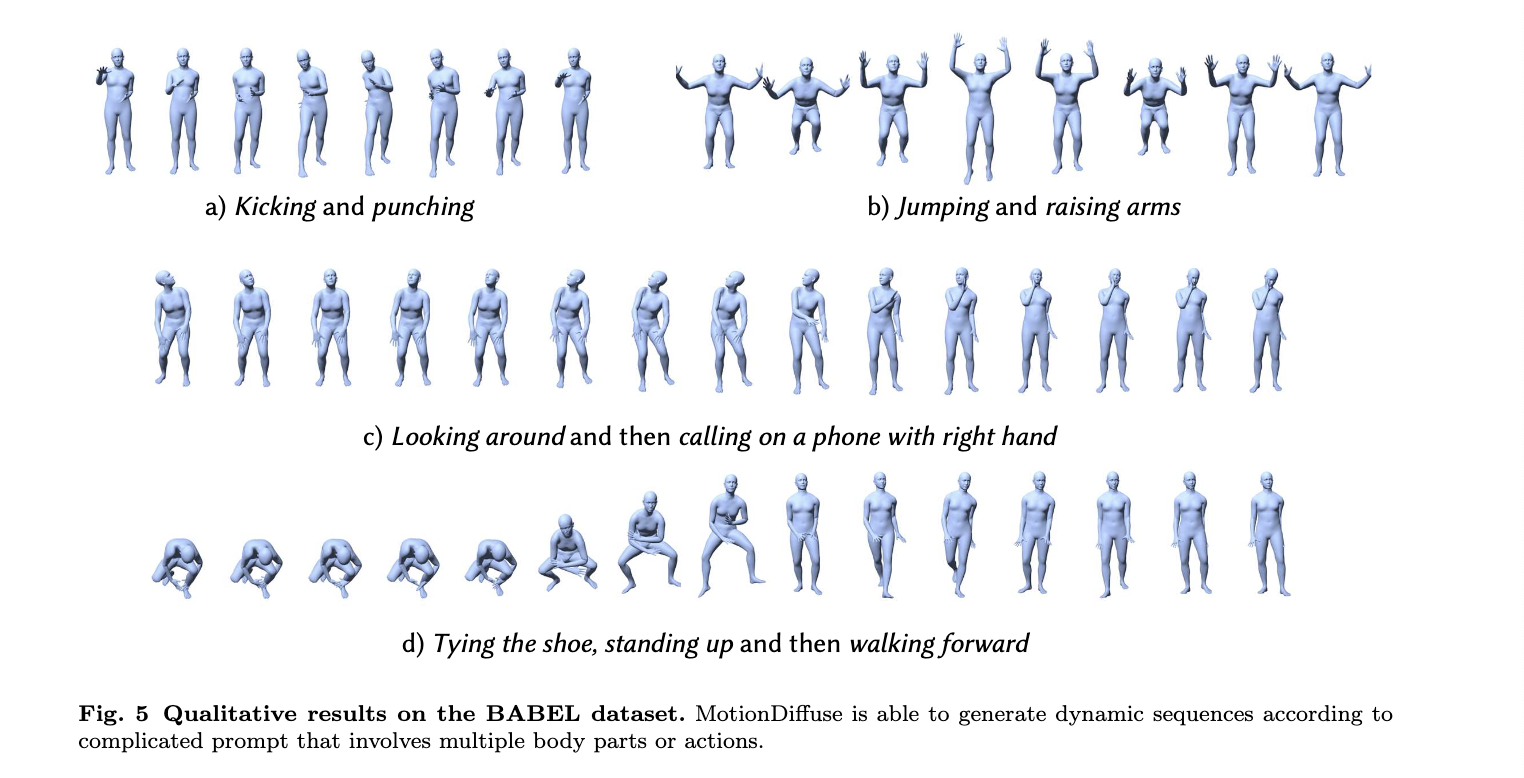
Conclusion, Limitations and Future Work
- 최초로 dissusion model을 이용한 Text-to-Motion
- 한계: 실시간 동작 불가능, 다양한 모션 표현 방식에 대한 일반화 문제
