BFS 문제 예제

BFS문제

연습문제1

문제소개

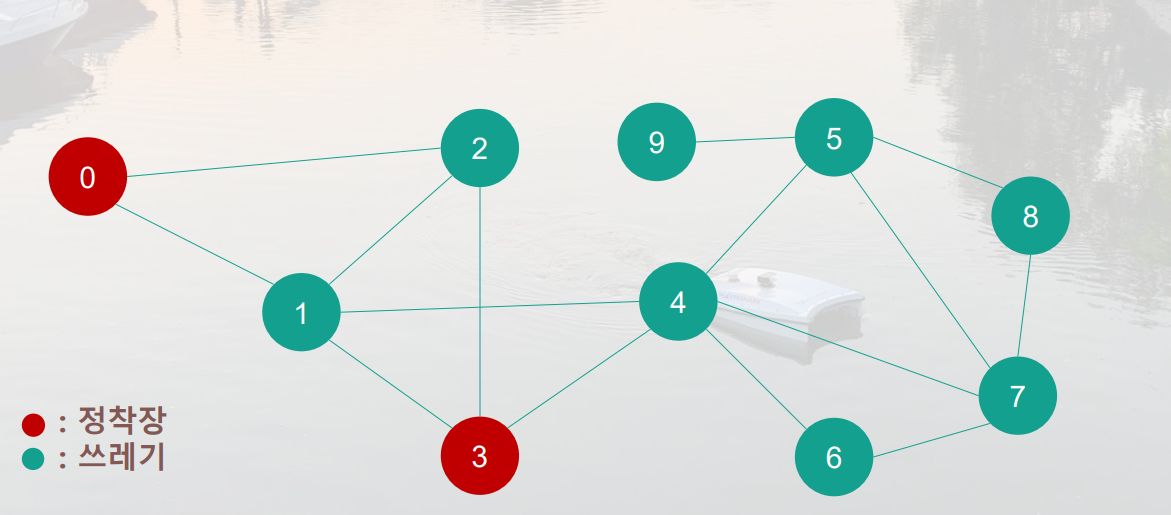
수거 로봇을 이용해 쓰레기를 수거한다.
쓰레기 로봇이 충전할 수 있는 정착장이 있다.
쓰레기와 쓰레기, 정착장과 쓰레기 거리는 모두 1KM로 동일하다.
각 쓰레기가 정착장과 얼마나 떨어져 있는지 구하여라

문제풀이

해당 문제의 그래프를 간단하게
v={0,1,2,3,4,5,6,7,8,9}
E={{0,1},{0,2},{1,2},{1,3},{1,4},{2,3},{3,4},{4,5},{4,6},{4,7},{5,7},{5,8},{5,9},{6,7},{7,8}}
로 나타낼 수 있다.
시작점을 기준으로 다른 각 노드들과의 거리를 구하는 문제이다. BFS 방법을 이용해서 문제를 해결할 수 있다.

• 시작점의 인근에 위치하는 노드들을 먼저 탐색한 후 해당 거리에 거리를 추가로 더하면서 쉽게 풀 수 있다.
• 정점간의 떨어진 거리를 나타내는 코드를 추가한다.

vector<int> dist;

• 각 정점간의 떨어진 거리는 모두 1KM로 동일하다.

dist[*iter] = dist[_s] + 1; 

• 출력코드를 추가해 준다.

for (int i = 0; i < n_vertices; ++i) {		
			cout << i << " : " << dist[i] << endl;
		}

위의 코드들을 BFS알고리즘에 추가하여 문제를 풀어보자!

문제코드

#include <iostream>
#include <queue>
#include <vector>
#include <list>
using namespace std;

class CGraph {
	int n_vertices;
	bool* visited;
	vector<list<int>> adj; 
	vector<int> dist; //정점간 얼마나 떨어져 있는지

public:
	CGraph(int _n) {
		this->n_vertices = _n;
		visited = new bool[_n];
		for (int i = 0; i < _n; ++i){
			visited[i] = false;
		}
		adj.resize(_n);
		dist.resize(_n);
	}
	~CGraph() {
		delete visited;
	}

	//방향이 없을 때
	void addUndirectedEdge(int _s, int _d) {
		adj[_s].push_back(_d);
		adj[_d].push_back(_s);
	}
	//방향을 넣어주고 싶을때
	void addEDirectedEdge(int _s, int _d) {
		adj[_s].push_back(_d);
	}

	//BFS 알고리즘
	void BFS(int _s) {
		visited[_s] = true;		// 시작점이니 _s는 당연히 방문했습니다. 
		queue<int> Q;			// 큐를 만들어 정점을 탐색하기 위한 준비를 합니다. 
		Q.push(_s);				// 우선 시작점 _s를 큐에 넣어줍니다. 
		
		int _s = 0;
		while (!Q.empty()) {
			_s = Q.front(); //stl에서는 pop사용 불가해서
			Q.pop(); //보는 얘랑 삭제하는 애랑 따로 구현
			list<int>::iterator iter; //저장된 값을 본다.
			for (iter = adj[_s].begin(); iter != adj[_s].end(); ++iter)//이터레이터 사용, 모든 원소를 본다.
				if (!visited[*iter]) //포인터로 표현해주어야 한다.
					Q.push(*iter);
			visited[*iter] = true;
			dist[*iter] = dist[_s] + 1; //거리 +1 적용추가
		}
        for (int i = 0; i < n_vertices; ++i) {		
			cout << i << " : " << dist[i] << endl;
		}
	}
};

int main() {
	CGraph OGraph(10);
	OGraph.addUndirectedEdge(0, 1);
	OGraph.addUndirectedEdge(0, 2);
	OGraph.addUndirectedEdge(1, 2);
	OGraph.addUndirectedEdge(1, 3);
	OGraph.addUndirectedEdge(1, 4);
	OGraph.addUndirectedEdge(2, 3);
	OGraph.addUndirectedEdge(3, 4);
	OGraph.addUndirectedEdge(4, 5);
	OGraph.addUndirectedEdge(4, 6);
	OGraph.addUndirectedEdge(4, 7);
	OGraph.addUndirectedEdge(5, 7);
	OGraph.addUndirectedEdge(5, 8);
	OGraph.addUndirectedEdge(5, 9);
	OGraph.addUndirectedEdge(6, 7);
	OGraph.addUndirectedEdge(7, 8);

	OGraph.BFS(3); //시작점 3

	return 0;
}

연습문제2

문제소개

수거 로봇을 이용해 쓰레기를 수거한다.
쓰레기 로봇이 충전할 수 있는 정착장이 2개 이상 존재한다.
쓰레기와 쓰레기, 정착장과 쓰레기 거리는 모두 1KM로 동일하다.
각 쓰레기가 가장 가까운 정착장과 얼마나 떨어져 있는지 구하여라

문제풀이

해당 문제의 그래프를 간단하게
v={0,1,2,3,4,5,6,7,8,9}
E={{0,1},{0,2},{1,2},{1,3},{1,4},{2,3},{3,4},{4,5},{4,6},{4,7},{5,7},{5,8},{5,9},{6,7},{7,8}}
로 나타낼 수 있다.
시작점을 기준으로 다른 각 노드들과의 거리를 구하는 문제이다. BFS 방법을 이용해서 문제를 해결할 수 있다. 연습문제1에서 사용한 정점간의 떨어진 거리를 이용하는 코드를 그대로 유지하며, 추가로 시작노드를 2개 이상이 되도록 코드를 추가 또는 수정한다.

• 시작점을 2개 이상 받아야 하기 때문에 파라미터를 동적으로 나타낼 수 있는 vector를 사용한다. 노드들은 정수로 표현되어 있어 int형으로 가져온다.

vector<int> _docks

• vector는 동적이기 때문에 시작점의 개수를 변수에 넣어 확인해주는 과정이 필요하다.

int n_docks = _docks.size();

• 모든 정점을 방문한 뒤에 시작점을 큐에 넣어주면 큐의 성질을 이용해서 2개 이상의 시작점을 표현할 수 있다.

for (int i = 0; i < n_docks; ++i) {
			visited[_docks[i]] = true;
			Q.push(_docks[i]); 
		}

위의 코드들을 BFS알고리즘에 추가하여 문제를 풀어보자!

문제코드

#include <iostream>
#include <queue>
#include <vector>
#include <list>
using namespace std;

class CGraph {
	int n_vertices;
	bool* visited;
	vector<list<int>> adj; 
	vector<int> dist; 

public:
	CGraph(int _n) {
		this->n_vertices = _n;
		visited = new bool[_n];
		for (int i = 0; i < _n; ++i){
			visited[i] = false;
		}
		adj.resize(_n);
		dist.resize(_n);
	}
	~CGraph() {
		delete visited;
	}

	//방향이 없을 때
	void addUndirectedEdge(int _s, int _d) {
		adj[_s].push_back(_d);
		adj[_d].push_back(_s);
	}
	//방향을 넣어주고 싶을때
	void addEDirectedEdge(int _s, int _d) {
		adj[_s].push_back(_d);
	}

	//BFS 알고리즘
	void BFS(vector<int> _docks) {
		int n_docks = _docks.size();	
		queue<int> Q;
		for (int i = 0; i < n_docks; ++i) {
			visited[_docks[i]] = true;	
			Q.push(_docks[i]);			
		}
		int _s = 0;
		while (!Q.empty()) {			
			_s = Q.front();
			Q.pop();
			list<int>::iterator iter;
			for (iter = adj[_s].begin(); iter != adj[_s].end(); ++iter) {
				if (!visited[*iter]) {
					visited[*iter] = true;
					Q.push(*iter);
					dist[*iter] = dist[_s] + 1;
				}
			}
		}
		for (int i = 0; i < n_vertices; ++i) {		
			cout << i << " : " << dist[i] << endl;
		}
	}
};

int main() {
	CGraph OGraph(10);
	OGraph.addUndirectedEdge(0, 1);
	OGraph.addUndirectedEdge(0, 2);
	OGraph.addUndirectedEdge(1, 2);
	OGraph.addUndirectedEdge(1, 3);
	OGraph.addUndirectedEdge(1, 4);
	OGraph.addUndirectedEdge(2, 3);
	OGraph.addUndirectedEdge(3, 4);
	OGraph.addUndirectedEdge(4, 5);
	OGraph.addUndirectedEdge(4, 6);
	OGraph.addUndirectedEdge(4, 7);
	OGraph.addUndirectedEdge(5, 7);
	OGraph.addUndirectedEdge(5, 8);
	OGraph.addUndirectedEdge(5, 9);
	OGraph.addUndirectedEdge(6, 7);
	OGraph.addUndirectedEdge(7, 8);
	vector docks = { 0, 3 }; //시작점 0, 3
	OGraph.BFS(docks);		
	return 0;

}