-
그래프 표현 방법(코드 중심)으로 설명합니다.
-
다익스트라 알고리즘을 설명하고, 코드를 구현합니다.
-
(옵션) 백준 알고리즘 다음 문제를 풀어봅니다.
-
1753 최단경로
-
1238 파티
-
1504 특정 최단 경로
-
1177 최소비용 구하기
- (옵션) BFS 관련 문제를 풀어 봅니다.
그래프 표현 방법
그래프를 표현하는 방법은 대표적으로 대표적인 인접행렬(adjacency matrix), 인접 리스트(adjacency list)로 나눌 수 있다. 그래프의 표현방법에 따라 그래프에 수행시키려는 연산과 이용하려는 응용의 차이를 가진다.
인접행렬(adjacency matrix)
하나의 정점에서 간선에 의해 직접 연결된 정점을 나타내는 인접 정점(adjacent vertex)을 정점의 개수가 n인 가로 세로 n x n 의 행렬M에 표현한다. 인접 정점 간의 간선이 존재할 때와 존재하지 않은 경우를 행렬M의 값으로 표현한다.
2차원 배열의 형태로 그래프를 표현
- 정점 i와 정점 j의 간선 존재O
M[i][j] = 1- 정점 i와 정점 j의 간선 존재X
M[i][j] = 0- 대각행렬은 모두 0
M[i][i] = 0 , M[j][j] = 0
- 무방향 그래프
인접행렬이 대칭 행렬이 된다. 배열의 상위 삼각이나 하위 삼각만 저장하면 메모리를 절약할 수 있음 - 방향 그래프
방향 그래프의 인접 행렬은 일반적으로 대칭이 아님 - 가중치 그래프
그래프의 간선들이 가중치를 가지고 있다면 행렬의 각 항목의 값이 달라진다. 간선들의 가중치는 반드시 양수이여야 한다.
-- 인접 정점 간의 간선이 존재O
0과 1이 아닌 해당 간선의 가중치의 값을 저장
-- 인접 정점 간의 간선이 존재X
매우 큰 값을 갖도록 하여 가중치로 나타날 수 있는 범위 밖의 값을 할당 -> INF
인접행렬을 이용한 그래프 구현
- 변수
정점의 개수, 정점, 인접 간선
int size; //정점의 개수
char vertices[]; //정점의 값
int adj[][]; //인접행렬의 정보- 메소드
AdjMatGraph() //생성자
bool isEmpty() //인접행렬의 간선 유무
bool isFull()
//정점
char insertVertex() //정점삽입
int deleteVertex()
//간선
int insertEdge( u, v) //간선삽입(무방향 그래프)
int deleteEdge( u, v)
int adjacent( v): int[]
//그래프 정보출력
display()그래프 구현을 위해 위와 같이 변수와 메소드를 구성해준다.
구현코드
#define MAX_VTXS 100
class AdjMatGraph {
protected:
int size;
char vertices[MAX_VTXS];
int adj[MAX_VTXS][MAX_VTXS];
public:
AdjMatGraph( ) { reset(); }
char getVertex(int i) { return vertices[i]; }
int getEdge(int i, int j) { return adj[i][j]; }
void setEdge(int i, int j, int val) { adj[i][j] = val; }
bool isEmpty(){ return size==0; }
bool isFull(){ return size>=MAX_VTXS; }
// 그래프 초기화 ==> 공백 상태의 그래프
void reset() {
size=0;
for(int i=0 ; i<MAX_VTXS ; i++ )
for(int j=0 ; j<MAX_VTXS ; j++ )
setEdge(i,j,0);
}
// 정점 삽입
void insertVertex( char name ) {
if( !isFull() ) vertices[size++] = name;
else printf("Error: 그래프 정점 개수 초과\n");
}
// 간선 삽입: 무방향 그래프의 경우임.
void insertEdge( int u, int v ) {
setEdge(u,v,1);
setEdge(v,u,1); }
// 그래프 정보 출력 (화면이나 파일에 출력)
void display( FILE *fp= stdout) {
fprintf(fp, "%d\n", size);// 정점의 개수 출력
for( int i=0 ; i<size ; i++ ) {// 각 행의 정보 출력
fprintf(fp,"%c ", getVertex(i));// 정점의 이름 출력
for( int j=0 ; j<size ; j++ )// 간선 정보 출력
fprintf(fp, " %3d", getEdge(i,j));
fprintf(fp,"\n");
}
}
};
인접 리스트(adjacency list)
모든 정점을 연결 리스트에 표현한다. 각 정정에 인접한 정점들을 리스트로 구현한다.
- 배열과 동적 가변 크기 배열(ArrayList), 연결리스트(LinkedLIst)를 이용해서 인접리스트를 표현
- 정점의 번호만 알면 번호를 배열의 인덱스로 하여 각 정점의 리스트에 쉽게 접근 가능
- 트리 구조라면 루트노드에서 다른 노드 한번에 접근 가능(사이클도 없고, 트리 구조 이기 때문)
- 그래프라면 루트노드에서 한번에 접근이 불가능 함
인접 리스트를 이용한 그래프 표현
간선을 포인터 변수를 이용해서 나타낸다. Node 클래스와 AdjListGraph 클래스로 구현해 상속을 통해 두 클래스를 사용한다.
Node 클래스
- 변수
id: int //node의 값
link: Node* //다음노드를 가르키는 포인터- 메소드
Node(int id) //생성자
getLink(): Node* //다음 노드의 포인터
setLink(Node* n)
display() AdjListGraph 클래스
- 변수
size: int //정점의 개수
vertices: char[] //정점의 정보
adj: Node*[] //각 정점의 인접리스트- 메소드
AdjListGraph () //생성자
isEmpty(): bool
isFull(): bool
//정점 추가 및 삭제
insertVertex(char v)
deleteVertex(int v)
//간선 추가 및 삭제
insertEdge(int u, int v)
deleteEdge(int u, int v)
adjacent(int v): Node*
display()구현코드
// 인접 리스트를 이용한 그래프: 노드 클래스
#define MAX_VTXS 100
class Node {
protected:
int id; // 정점의 id
Node* link; // 다음 노드의 포인터
public:
Node(int i, Node *l=NULL) : id(i), link(l) { }
~Node() {
if( link != NULL ) delete link;
}
int getId() { return id; }
Node* getLink() { return link; }
void setLink(Node* l) { link = l; }
};
// 연결 리스트를 위한 노드 그래프 클래스 포함
class AdjListGraph {
protected:
int size; // 정점의 개수
char vertices[MAX_VTXS]; // 정점 정보
Node* adj[MAX_VTXS]; // 각 정점의 인접 리스트
public:
AdjListGraph() : size(0) { }
~AdjListGraph(){ reset(); }
void reset(void) {
for( int i=0 ; i<size ; i++ )
if( adj[i] != NULL ) delete adj[i];
size = 0;
}
void insertVertex( char val ) { // 정점 삽입 연산
if( !isFull() ) {
vertices[size] = val;
adj[size++] = NULL;
}
else printf("Error: 그래프 정점 개수 초과\n");
}
void insertEdge( int u, int v) { // 간선 삽입 연산
adj[u] = new Node (v, adj[u]); // 인접 리스트에 추가
adj[v] = new Node (u, adj[v]); // 방향 그래프 ==> 주석 처리함
}
void display( ) {
printf("%d\n", size); // 정점의 개수 출력
for( int i=0 ; i<size ; i++ ) { // 각 행의 정보 출력
printf("%c ", getVertex(i)); // 정점의 이름 출력
for( Node *v=adj[i] ; v != NULL ; v=v->getLink() )
printf(" %c", getVertex(v->getId()) );
printf("\n");
}
}
Node* adjacent(int v) { return adj[v]; }
void insertEdge( int u, int v) { // 간선 삽입 연산
adj[u] = new Node (v, adj[u]); // 인접 리스트에 추가
adj[v] = new Node (u, adj[v]); // 방향 그래프 ==> 주석 처리함
}
void display( ) {
printf("%d\n", size); // 정점의 개수 출력
for( int i=0 ; i<size ; i++ ) { // 각 행의 정보 출력
printf("%c ", getVertex(i)); // 정점의 이름 출력
for( Node *v=adj[i]; v != NULL; v=v->getLink() )
printf(" %c", getVertex(v->getId()) );
printf("\n");
}
}
Node* adjacent(int v) { return adj[v]; }
bool isEmpty() { return size ==0; }
bool isFull() { return size >= MAX_VTXS; }
char getVertex( int i ) {return vertices[i]; }
}; // end of class AdjListGraph
다익스라 알고리즘(Dijkstra)
설명
• 시작 정점 v에서 다른 모든 정점까지의 최단 경로를 찾는 알고리즘
▪ 시작 정점 v
▪ 집합 S : v에서부터의 최단경로를 이미 찾은 정점들의 집합
▪ dist[u] 배열: S에 있는 정점들 만을 거쳐서 가는 v-u 간 경로의 길이
▪ 초기값
- S={v}
- dist[u] = v-u간에 간선이 있으면 weight(v,u) 그렇지 않으면 무한대
▪ 알고리즘 - 매 단계에서 S안에 있지 않은 정점들 중에서 가장 dist 값이 작은 정점을 S에 추가
- S에 포함되지 않은 남은 정점들의 dist 값 갱신
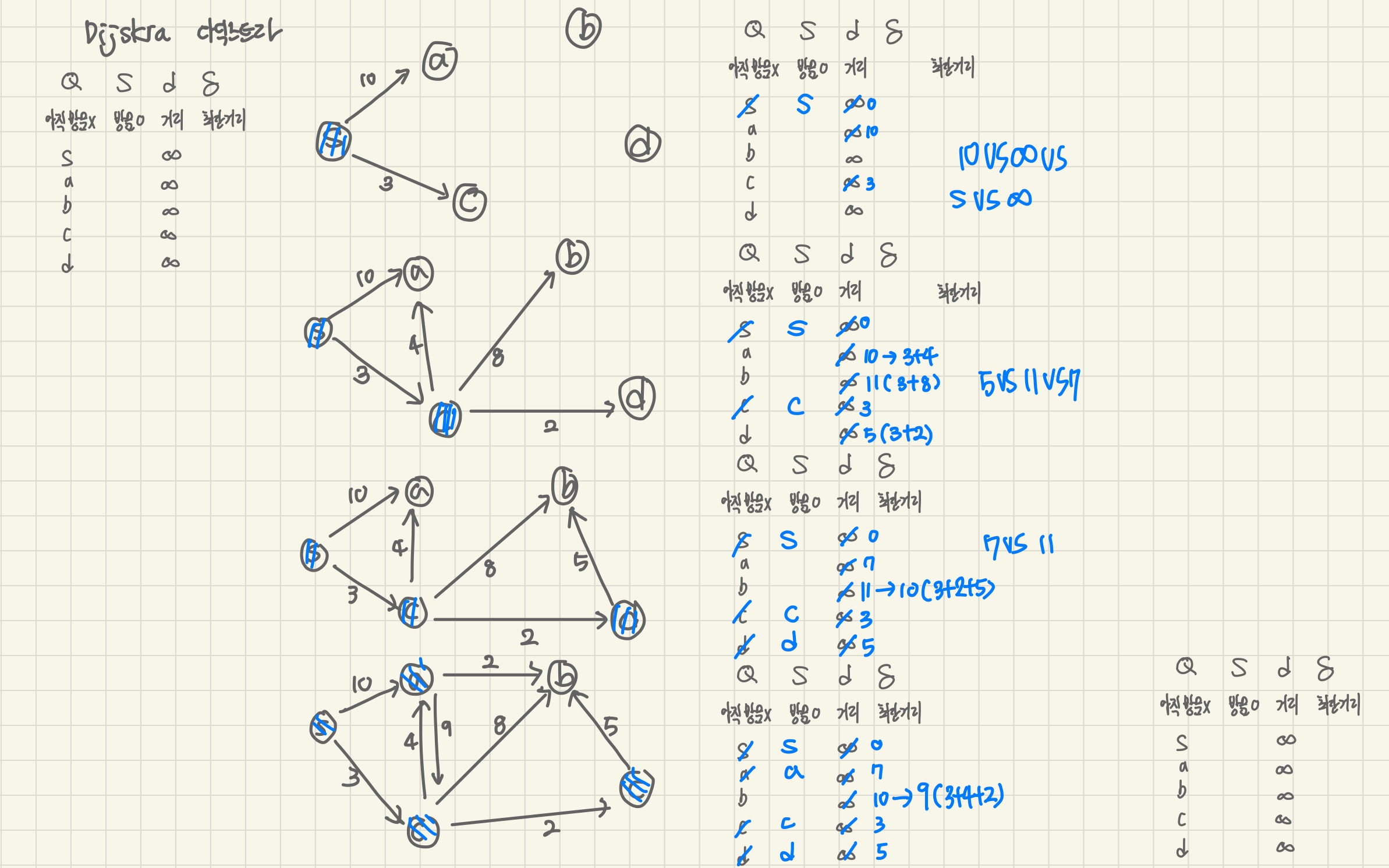
pseudo code
shortest_path_dijkstra(v)
S <- {v}
for 각 정점 w in G do
dist[w] = weight[v][w]
while 모든 정점이 S에 포함되지 않으면 do
u <- 집합 S에 속하지 않는 정점 중에서 최소 dist를 갖는 정점 선택
S <- S union {u}
for u에 인접하고 S에 있지 않은 모든 정점 w do
if ( dist[u] + weight[u][w] < dist[w] )
then dist[w] dist[u] + weight[u][w]코드구현
// Dijkstra알고리즘의 최단 경로 탐색 기능이 추가된 그래프
class WGraphDijkstra : public WGraph {
int dist[MAX_VTXS]; // 시작노드로부터의 최단경로 거리
bool found[MAX_VTXS]; // 방문한 정점 표시 → 집합 S
public:
int chooseVertex() { // 가장 비용 적은 미방문 정점을 반환
int min = INF;
int minpos = -1;
for( int i=0 ; i<size ; i++ )
if( dist[i]< min && !found[i] ){
min = dist[i];
minpos = i;
}
return minpos;
}
void printDistance() { //모든 정점들의 dist[] 값 출력
for( int i=0 ; i<size ; i++)
printf("%5d", dist[i]);
printf("\n");
}
// Dijkstra의 최단 경로 알고리즘: start 정점에서 시작함.
void ShortestPath( int start ) {
for( int i=0 ; i<size ; i++) { //초기화: dist[], found[]
dist[i] = getEdge(start,i); //인접행렬 값 반환(간선 가중치)
found[i] = false; //처음에 S집합은 비어있음.
}
found[start] = true; // S에 포함
dist[start] = 0; // 최초 거리
for( int i=0 ; i<size ; i++ ){
printf("Step%2d:", i+1);
printDistance(); // 모든 dist[] 배열값 출력
int u = chooseVertex(); // S에 속하지 않은 비용 가장 작은 정점 반환
found[u] = true; // 집합 S에 포함
for( int w=0 ; w<size ; w++) {
if( found[w] == false )//S에 속하지 않는 노드 w의 dist값 갱신
if( dist[u] + getEdge(u,w) < dist[w] )
dist[w] = dist[u] + getEdge(u,w);
} // u를 거쳐가는 것이 최단 거리이면 dist[] 갱신
}
}
};문제
1753 최단경로
문제소개

문제풀이
주어진 시작점에서 다른 모든 정점으로의 최단 경로를 구해야 한다. 최단 경로의 경로값, 즉 최소비용을 구하도록 한다. 다익스트라 알고리즘을 이용한다.
(배열만으로 구현하는 방법과 우선순위큐를 이용하는 방법으로 나뉜다.
배열으로만 구현하는 방법은 메모리 초과가 발생한다!(포스팅 참고))
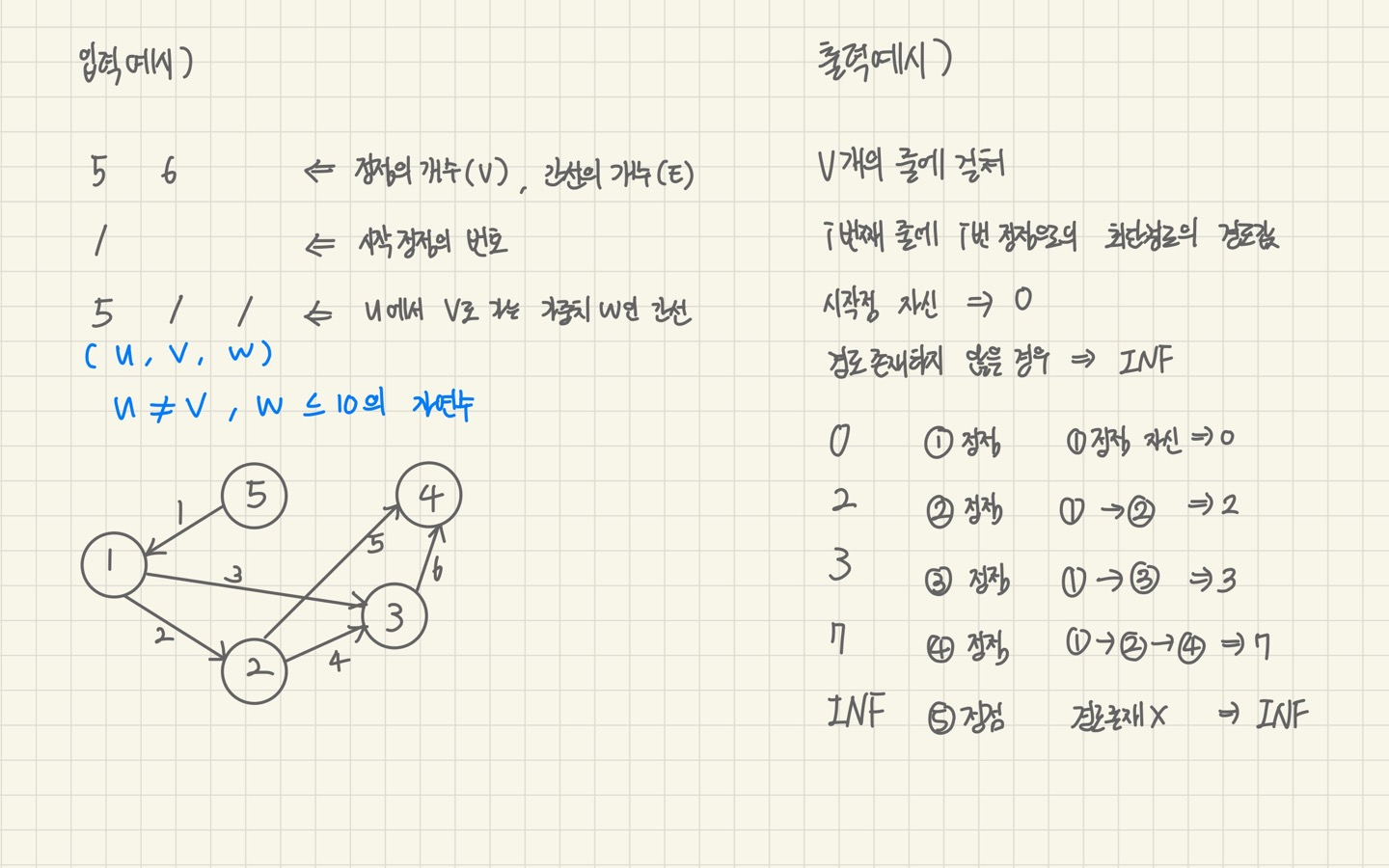
문제코드
int V; //정점의 개수
int E; //간선의 개수
int start; //시작정점의 번호
int dist[MAX]; //가중치
vector<pair<int, int>> vertex[MAX]; //출발정점과 도착정점을 pair로 묶는다.
void input() //입력값 가져오기
{
cin >> V >> E >> Start;
for (int i = 0; i < E; i++)
{
int a, b, c;
cin >> a >> b >> c;
Vertex[a].push_back(make_pair(b, c));
}
for (int i = 1; i <= V; i++) Dist[i] = INF;
}
void Solution() //우선순위큐를 이용한다.
{
priority_queue<pair<int, int>> PQ;
PQ.push(make_pair(0, Start));
Dist[Start] = 0;
while (PQ.empty() == 0)
{
int Cost = -PQ.top().first;
int Cur = PQ.top().second;
PQ.pop();
for (int i = 0; i < Vertex[Cur].size(); i++)
{
int Next = Vertex[Cur][i].first;
int nCost = Vertex[Cur][i].second;
if (Dist[Next] > Cost + nCost)
{
Dist[Next] = Cost + nCost;
PQ.push(make_pair(-Dist[Next], Next));
}
}
}
for (int i = 1; i <= V; i++)
{
if (Dist[i] == INF) cout << "INF" << endl;
else cout << Dist[i] << endl;
}
}
void Solve()
{
Input();
Solution();
}
int main(void)
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
//freopen("Input.txt", "r", stdin);
Solve();
return 0;
}1238 파티
문제소개

문제풀이
단순한 다익스트라 문제와 달리 최단거리로 목적지, 즉 도착정점까지 이동해 다시 출발 지점으로 되돌아오는 최단거리를 구해야 한다.
정점들의 정보를 입력 받을 때 역방향의 간선을 따로 입력 받아 최단거리를 구할 수 있다.
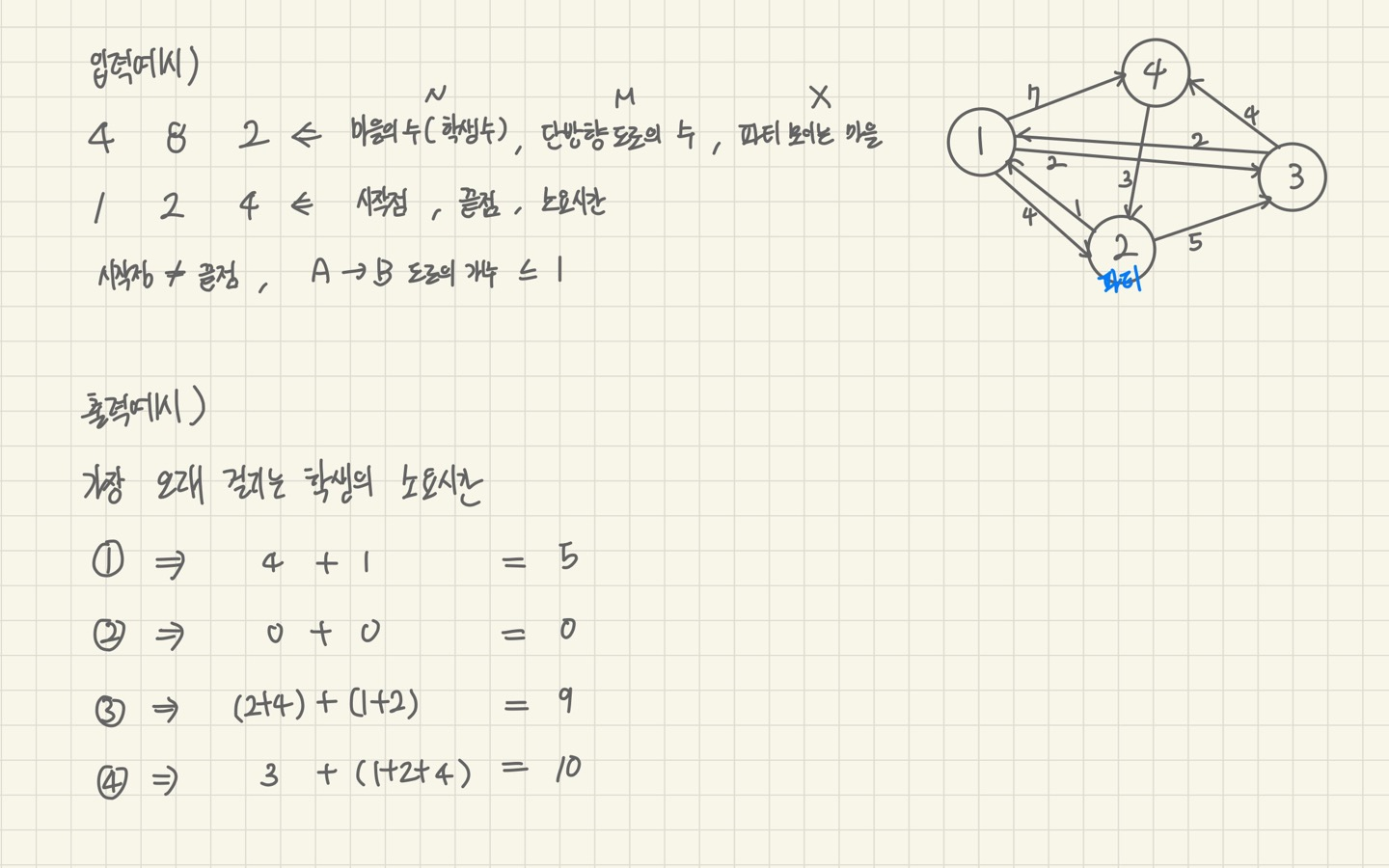
문제코드
#define pii pair<int, int>
int N; //마을의 수(학생의 수)
int M; //단방향 도로의 개수
int X; //파티을 위해 모이는 마을의 번호
const int INF = 1e9+7;
vector<pii> graph[1001]; //pair를 적용한다.
vector<int> dist;
int resdist[1001]; //가중치 반영
void input(){ //입력값 받아오기
int u, v, t; //첫줄 입력값
cin >> N >> M >> X;
for(int i = 0; i < M; i++){
cin >> u >> v >> t;
graph[u].push_back(make_pair(t, v)); //pair적용해서 간선의 출발정점과 도착정점을 표현한다.
}
}
void Dijstra(int S){ //다익스트라 알고리즘
dist.clear(); //가중치 비운다.
dist.resize(N+1, INF);
dist[S] = 0;
priority_queue<pii, vector<pii >, greater<pii > > que;
que.push({0, S});
while(!que.empty()){
int min_cost = que.top().first;
int now = que.top().second;
que.pop();
if(min_cost > dist[now]) continue;
for(int i = 0; i < graph[now].size(); i++){
int next = graph[now][i].second;
int next_cost = min_cost + graph[now][i].first;
if(next_cost < dist[next]){
dist[next] = next_cost;
que.push({next_cost, next});
}
}
}
}
int main(){
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
input();
for(int i = 1; i <= N; i++){
Dijstra(i);
// i가 X로 가는 최단거리 half
resdist[i] = dist[X];
}
Dijstra(X);
int res = 0;
for(int i = 1; i <= N; i++){
resdist[i] += dist[i];
res = max(res, resdist[i]);
}
cout << res;
return 0;
}
1504 특정 최단 경로
문제소개

문제풀이
문제코드
11779 최소비용 구하기
문제소개

문제풀이
문제코드
BFS 적용 문제
해당 링크를 통해서 BFS 적용 문제를 확인할 수 있다.
https://velog.io/@ehekaanldk/BFS-%EB%AC%B8%EC%A0%9C-%EC%98%88%EC%A0%9C
