DeepML. Neural Network - 2

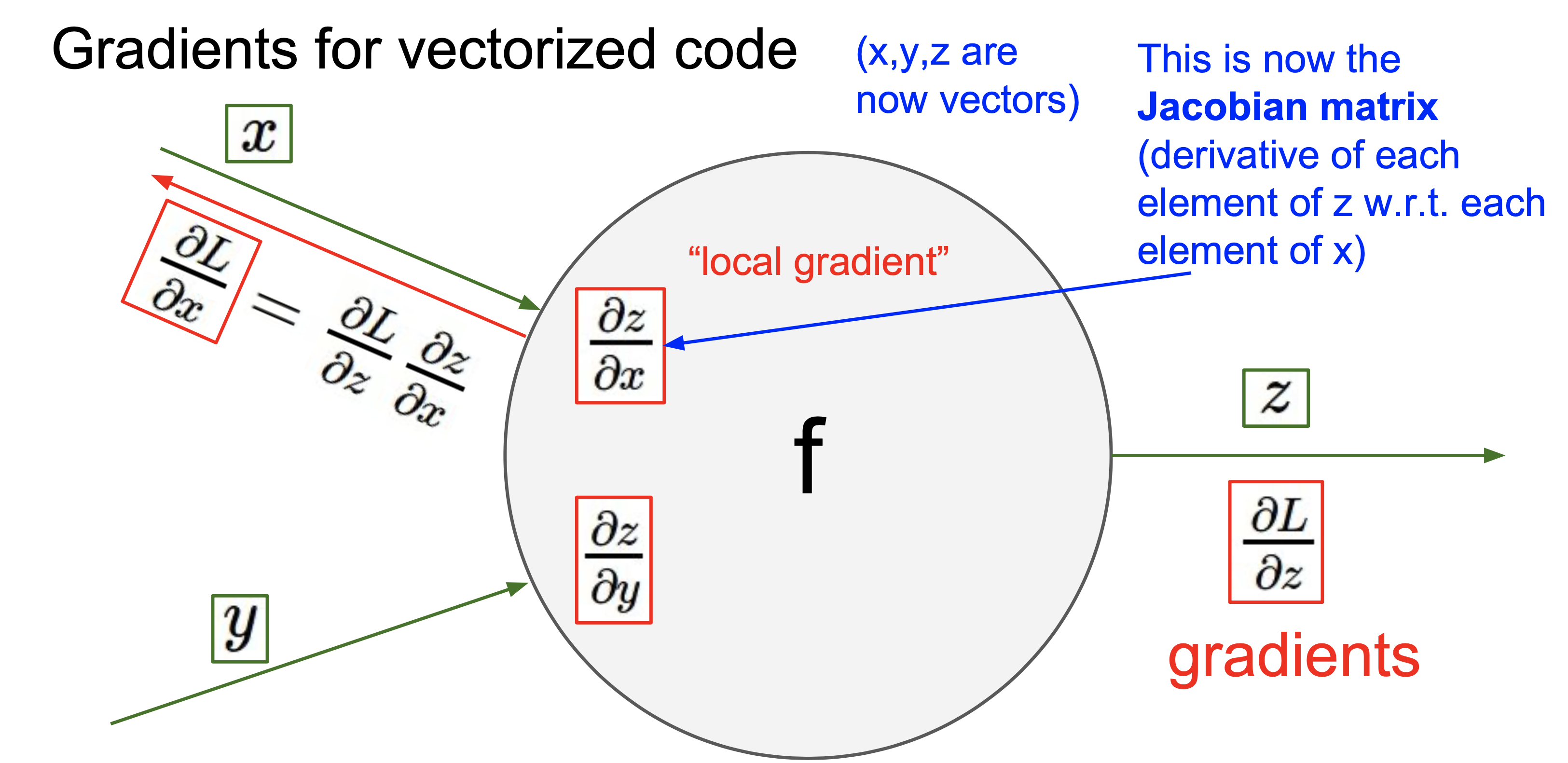
위는 벡터인 경우 연산을 대략적으로 그린 그림이다.

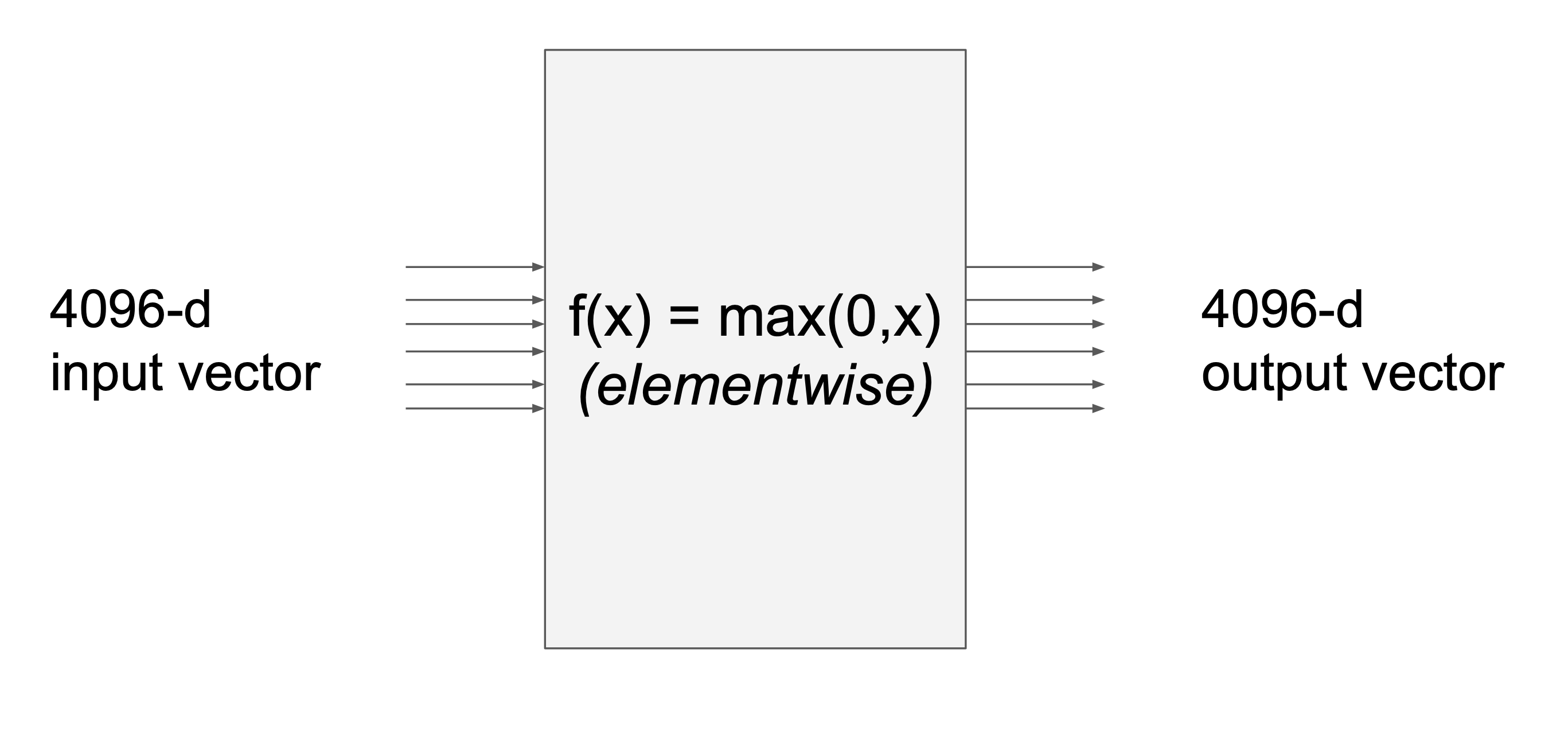
위와 같은 연산이 있다고 생각해보자.
여기서 Jacobian matrix는 $\partial f \over \partial x$이다.

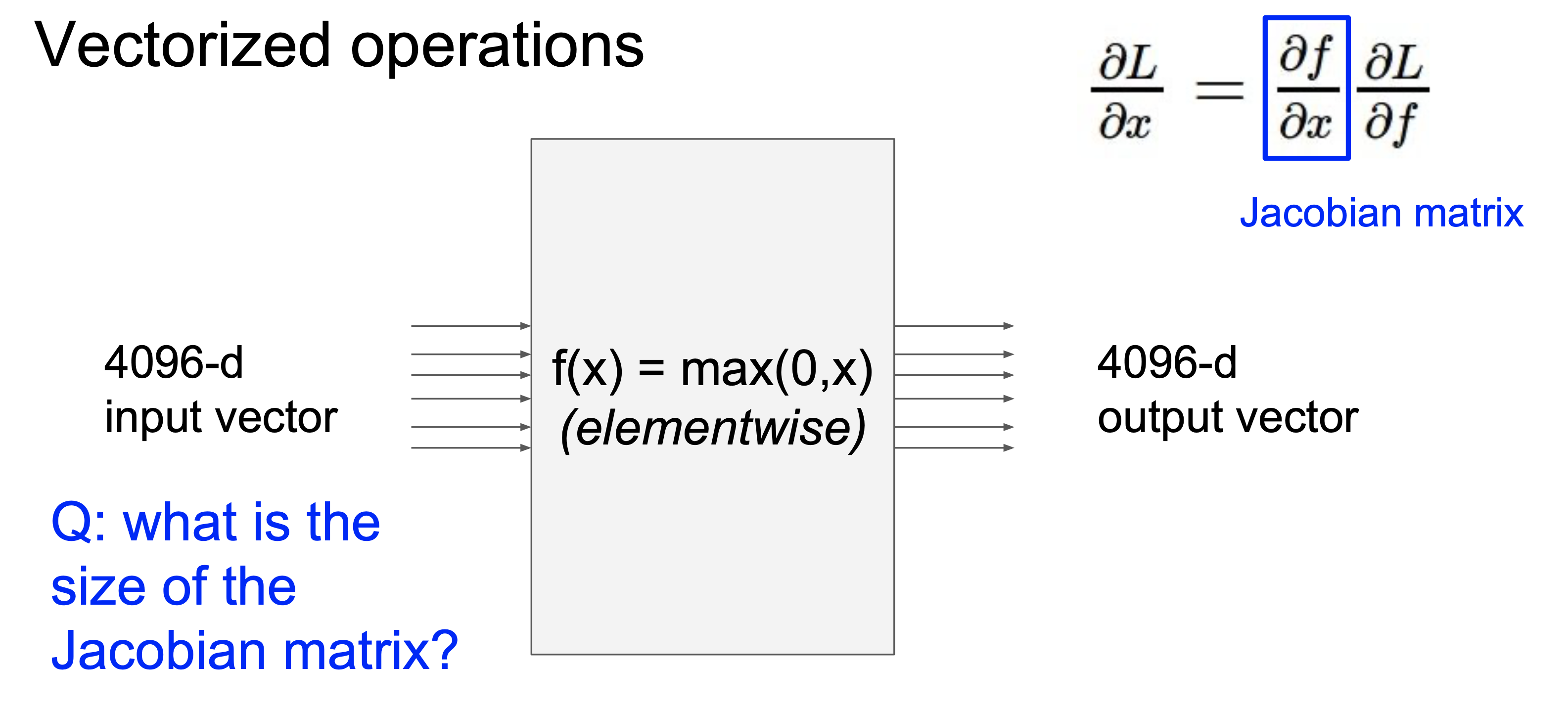
이때 Jacobian matrix의 사이즈는 4096x4096 이다. 이때 Jacobian matrix는 diagonal matrix(대각행렬)의 형태를 띈다.
출력 $x$의 영향에 대해서, 그리고 이값을 사용하는 것에 대해서만 알면된다. 그리고 우리가 계산한 gradient값을 채워넣으면 된다.

또 다른 예제

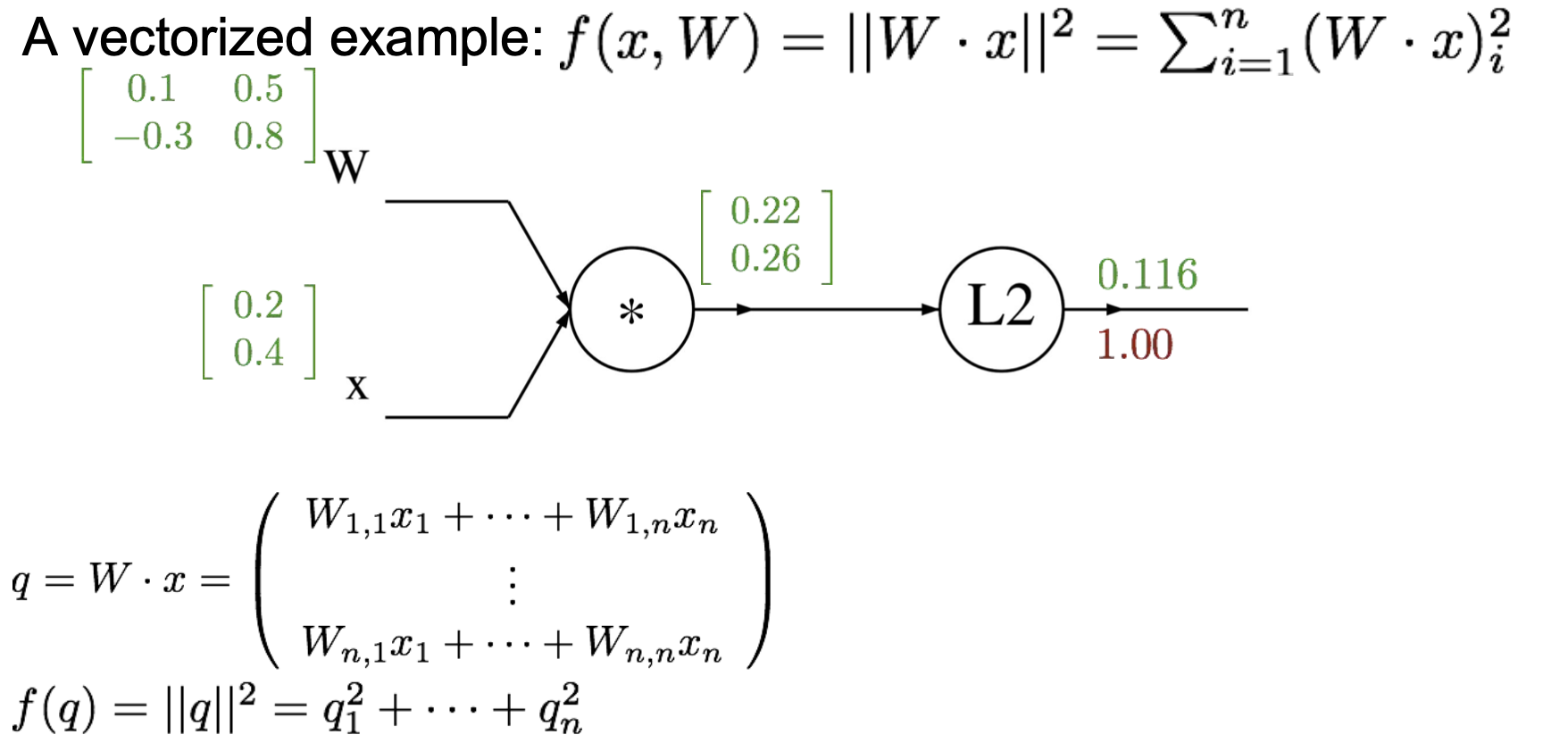
밑에와 같은 $W$, $X$벡터를 가진 예제가 있다.

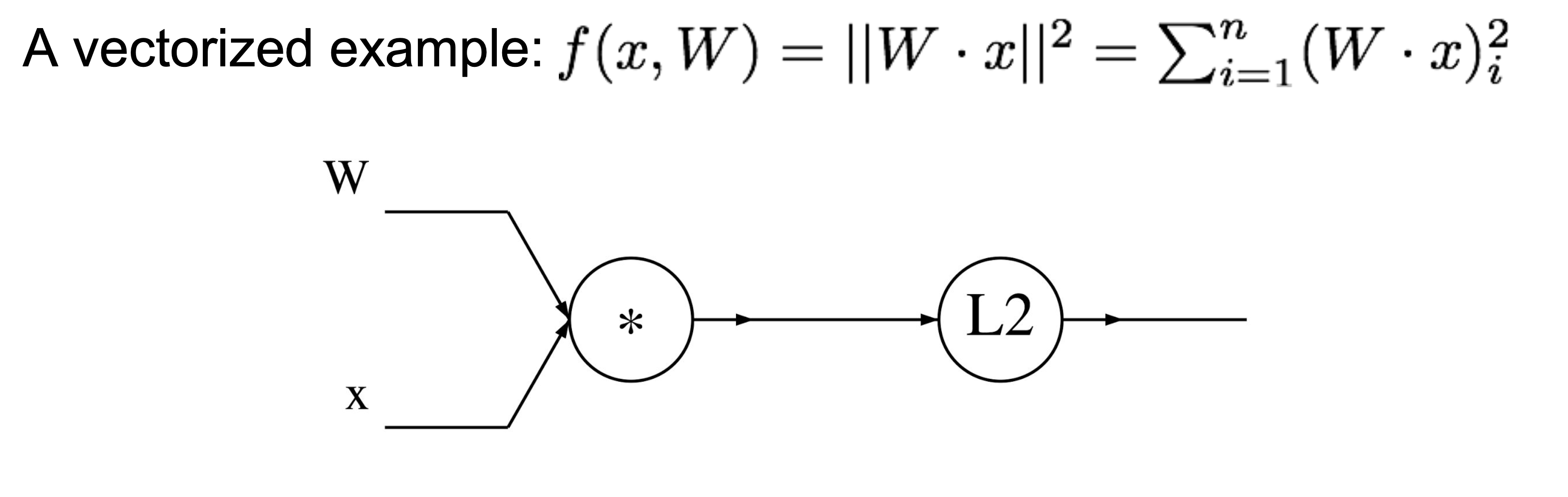
각각 $\partial {f} \over \partial {q_i}$,$\partial {q_k} \over \partial W_{i,j}$, $\partial {q_k} \over \partial x_{i}$과 같은 local gradient값을 간소화해서 나타내면,
$\nabla_q f = 2q$
$\nabla_W f = 2q\cdot x^T$
$\nabla_x f = 2W^T\cdot q$
처럼 나타낼 수 있다. gradient가 무엇인지 계산했으면 이것들이 변수의 모양과 동일한지 확인해야한다. 검사하는데 유용할 것이다.

[forward/backward pass API]
위의 식과 그래프를 바탕으로 코드를 구현해보면 아래와 같다.

각 노드를 local하게 보았고, upstream gradient와 함께 chain rule을 이용해서 local gradient를 계산했다.

• forward pass : 노드의 출력을 계산하는 함수를 구현한다.
• backward pass : gradient를 계산한다. chain rule을 이용.

Summary

• 신경망은 크고 복잡해서 모든 파라미터에 일일히 gradient하는 것은 비효율적이며, 그래서 gradient를 계산하기 위해 backpropagation을 사용한다.
• 이것은 신경망의 핵심 기술이고, 뒤에서 부터 거슬러 올라가며, 입력이나 파라미터 등등 모든 중간 변수들을 구하기 위해, 그리고 각각의 노드에 대한 그래프 구조의 구현이 실제로 얼마나 큰지 이것들을 forward, backward API구현으로 나타내느지에 대해 이야기 했다.
• forward pass에서 연산 결과를 계산 후 저장하며, 이것은 나중에 우리가 gradient를 계산할 때 backward pass에서 chain rule을 사용하기 위함이다.
• upstream gradient와 저장한 값들을 곱해 각 노드의 input에 대한 gradient를 구한다. 그리고 그것들을 연결된 이전 노드로 통과시킨다.

Neural networks

우리 뇌 속에 있는 뉴런을 나타내는 그림이다.

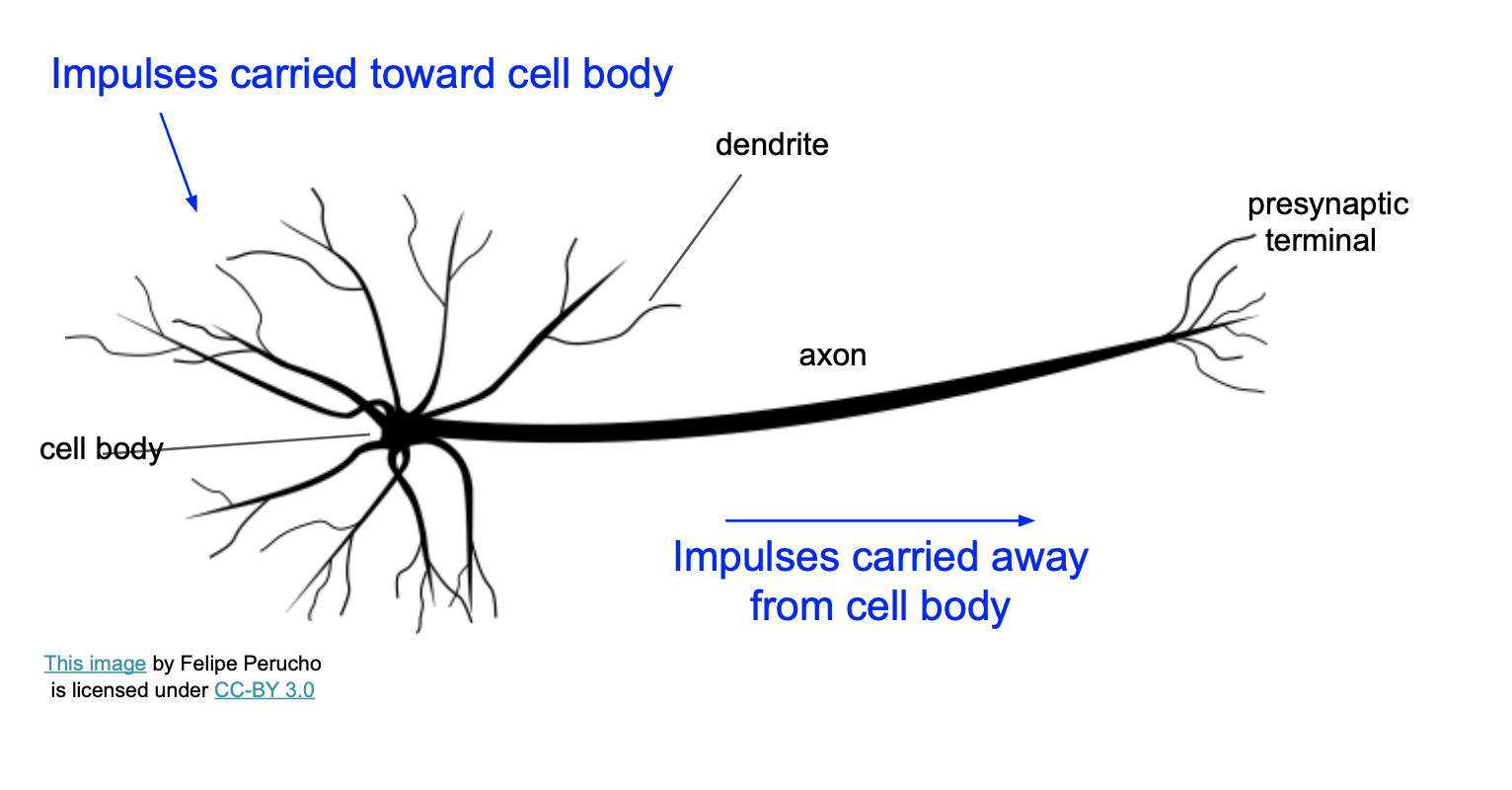
위 뉴런을 computational graph로 나타낸 그림이다.

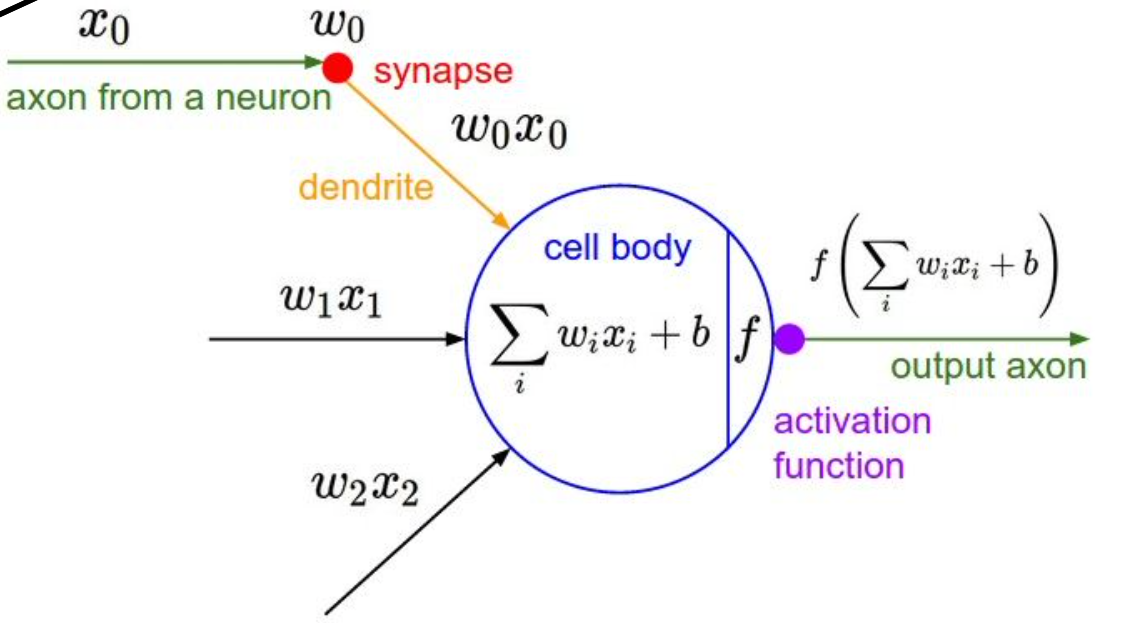
활성화 함수는 sigmoid를 예를 들겠다.

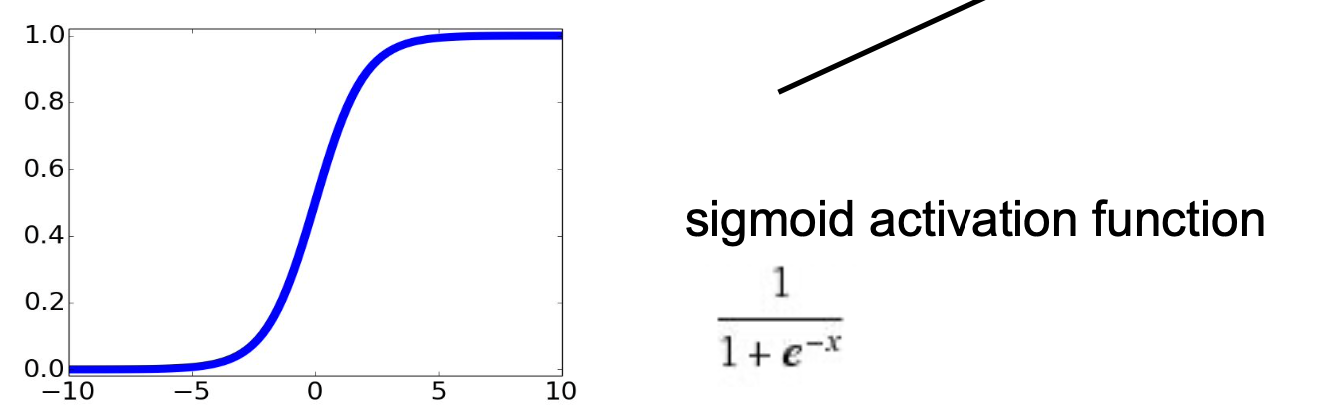
sigmoid를 이용한 신호를 함수로 구현하면 아래와 같다.

물론 sigmoid보단 ReLU를 가장 많이 사용하는 추세이다. 다양한 activation functions이 있다.

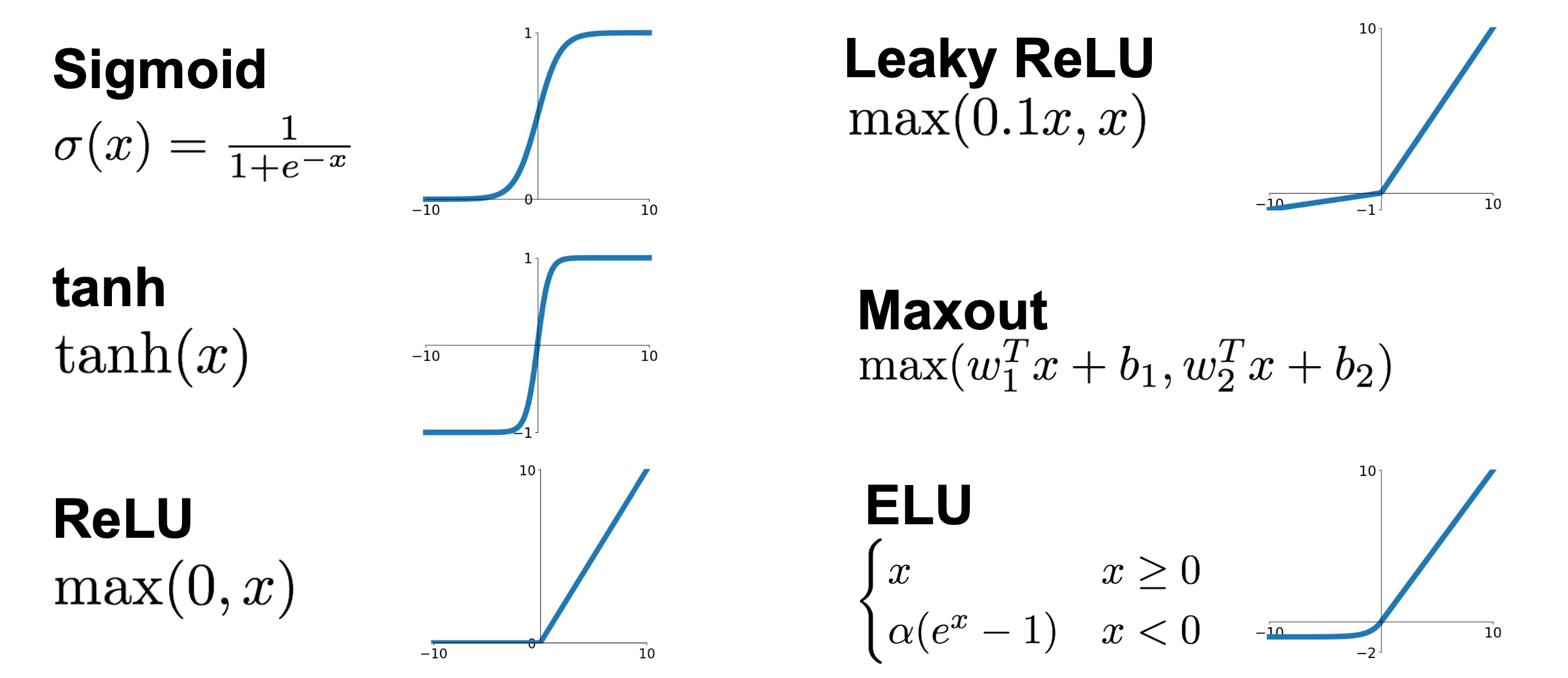
구조(Architectures)를 살펴보자.

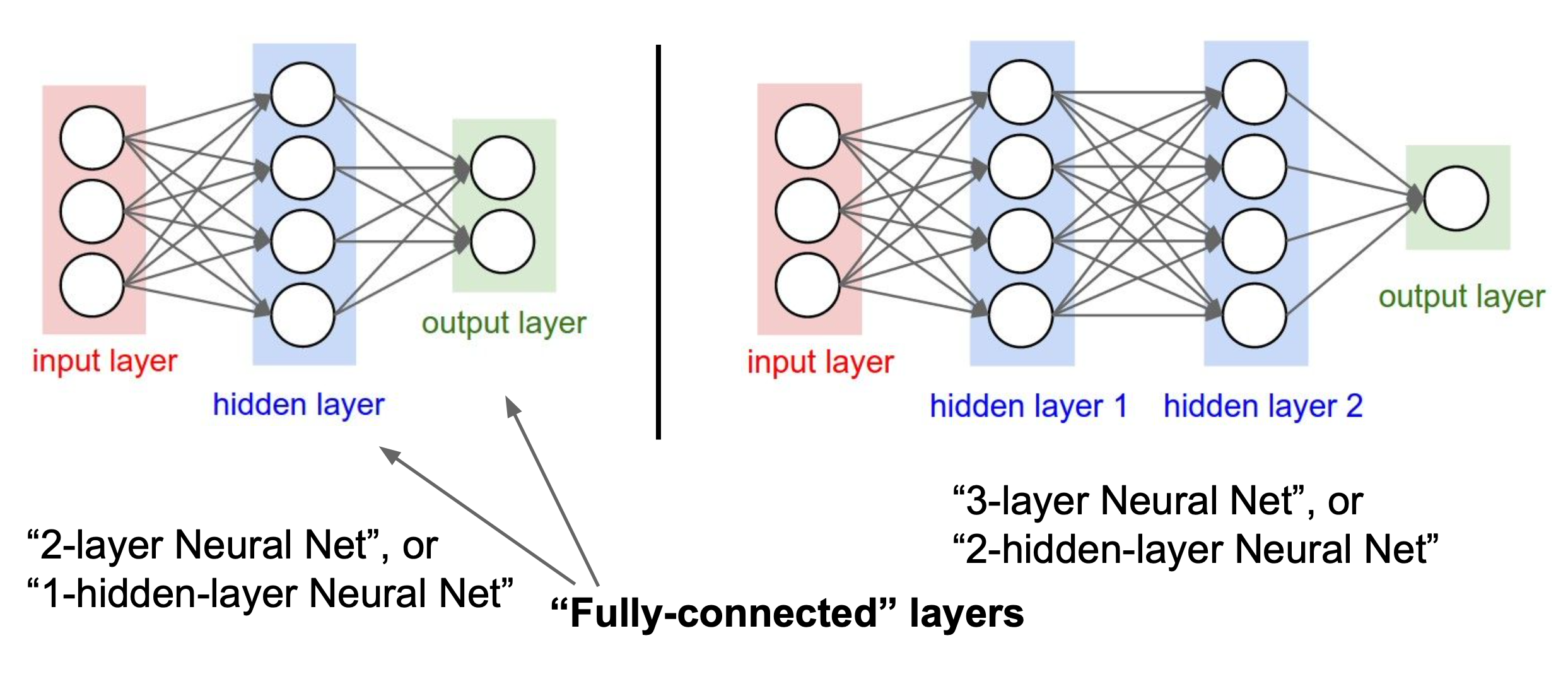
위의 3-layer를 코드로 나타내면 아래와 같다.

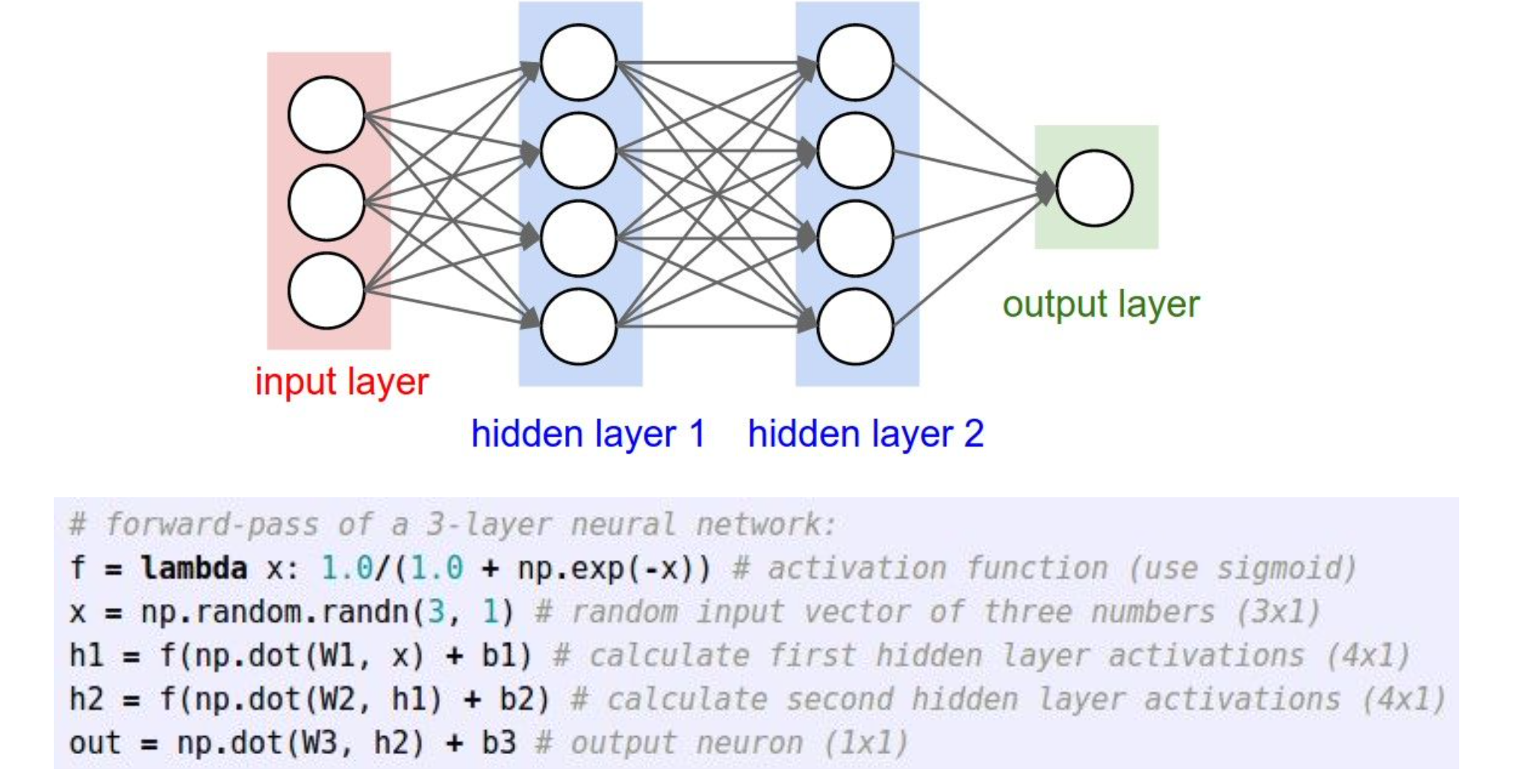
Summary

• we arrange neurons into fully-connected layers.
• Neural networks are not really neural.
• The abstraction of a layer has the nice property that
  it allows us to use efficient vectorized code.