scores function
는 score vector(output)이며 는 input이다.
SVM loss
data loss + regularization
여기서 우리가 원하는 것은
최적의 loss를 갖게하는 파라미터 를 찾는것이다.
Optimization
최적의 를 찾는 것이다.
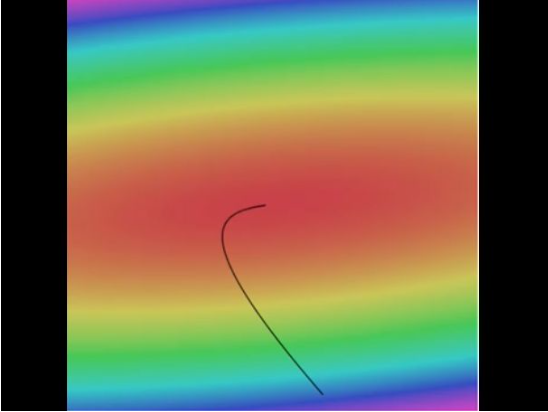
gradient가 음수인 방향, 즉 경사가 하강하는 방향을 반복적으로 구해 아래로 나아갈 수 있고, 가장 낮은 loss를 찾게 될 것이다.
[Vanilla Gradient Descent]
while True:
weights_grad = evaluate_gradient(loss_fun, data, weights)
weights += -step_size * weights_gradGradient descent
- Numerical gradient : slow, approximate, easy to write
- Analytic gradient : fast, exact, error-prone
Computational graphs
임의의 복잡한 함수를 통해 어떻게 analytic gradient를 계산하는지에 대해 이야기 할 것이며, computational graph라는 기법을 사용할 것이다.
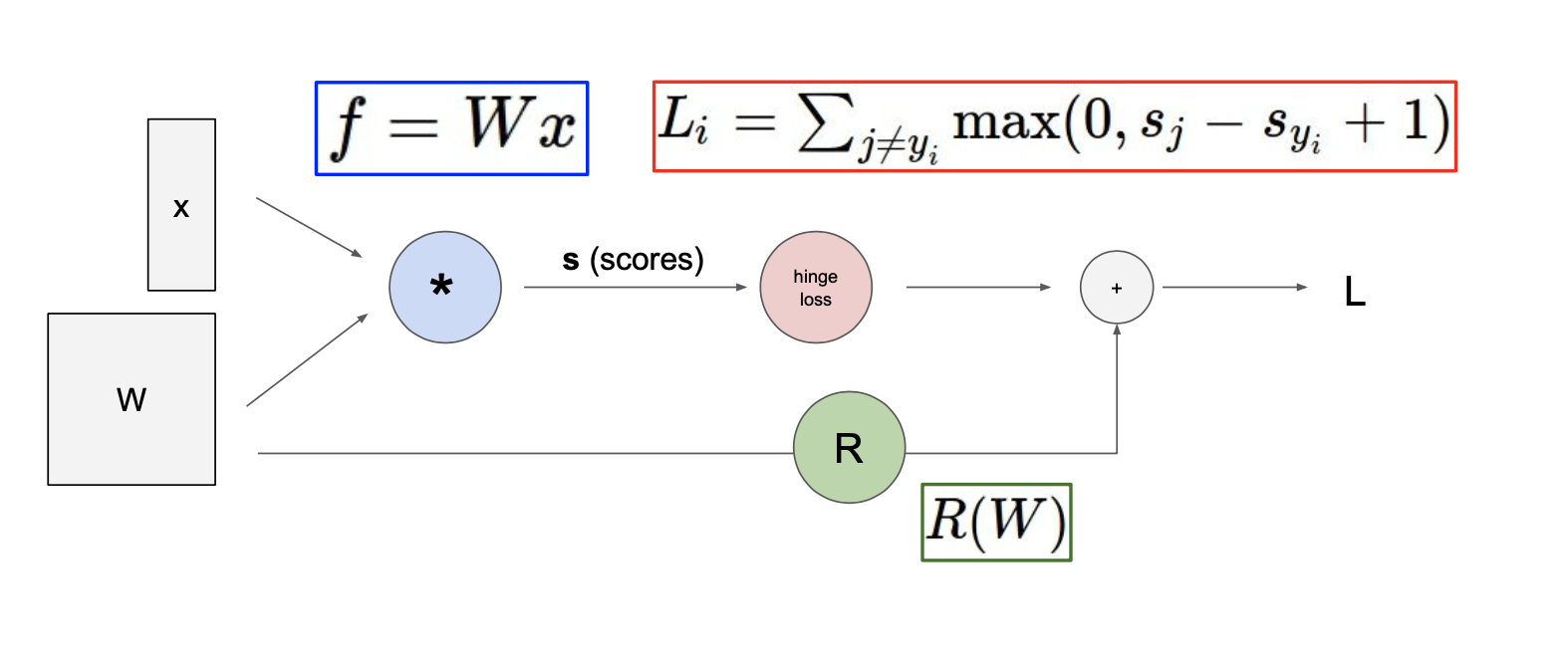
위의 예제는 input이 , 인 linear classifier이다.
Computational graphs를 사용해서 함수를 표현하게 됨으로써 backpropagation이라고 부르는 기술을 사용할 수 있게 되며, backpropagation은 gradient를 얻기위해 computational graph 내부의 모든 변수에 대해 chain rule을 재귀적으로 사용한다.
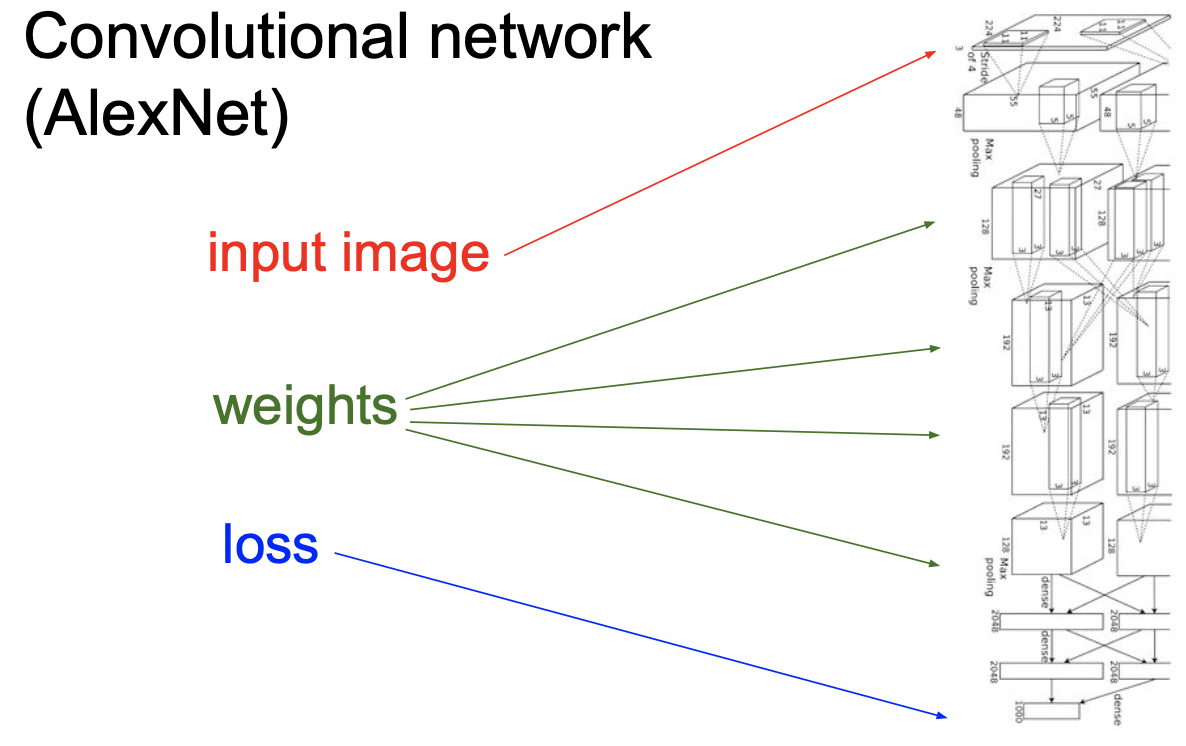
Convolutional Network
[AlexNet]
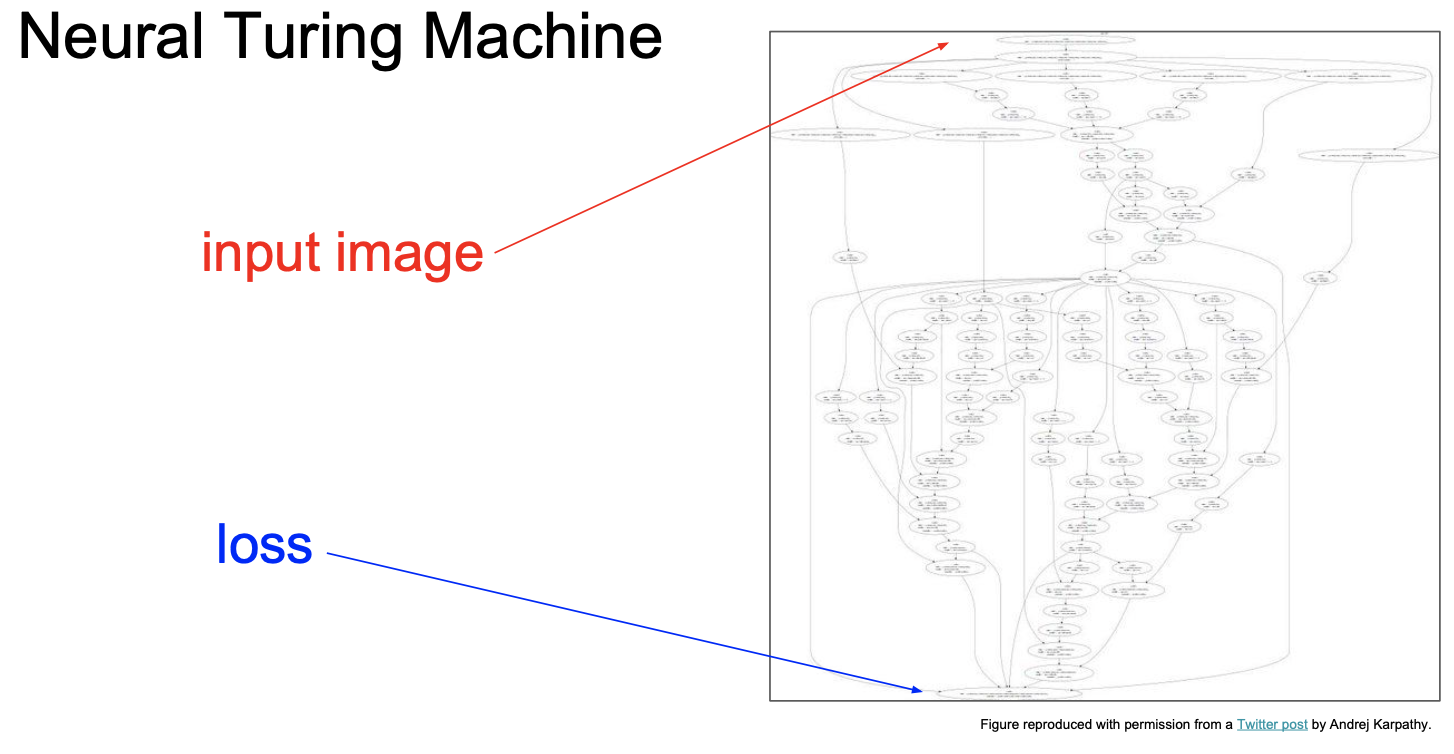
[Neural Turing Machine]
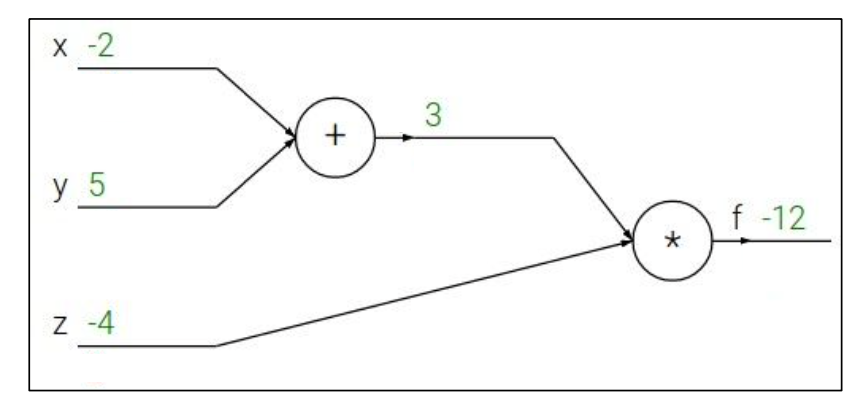
Backpropagation sample example 1
eg. x=-2, y=5, z=-4
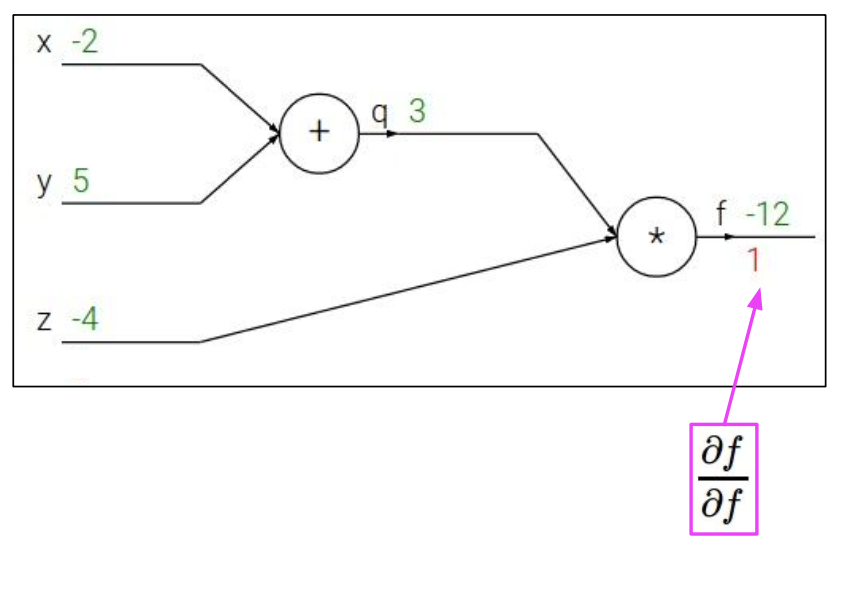
function f의 출력에 대한 어떤 변수의 gradient를 찾길 원한다.
우리는 ,, 을 구하고 싶다.
backpropagation은 chain rule의 재귀적인 응용이므로 뒤에서부터 시작한다.
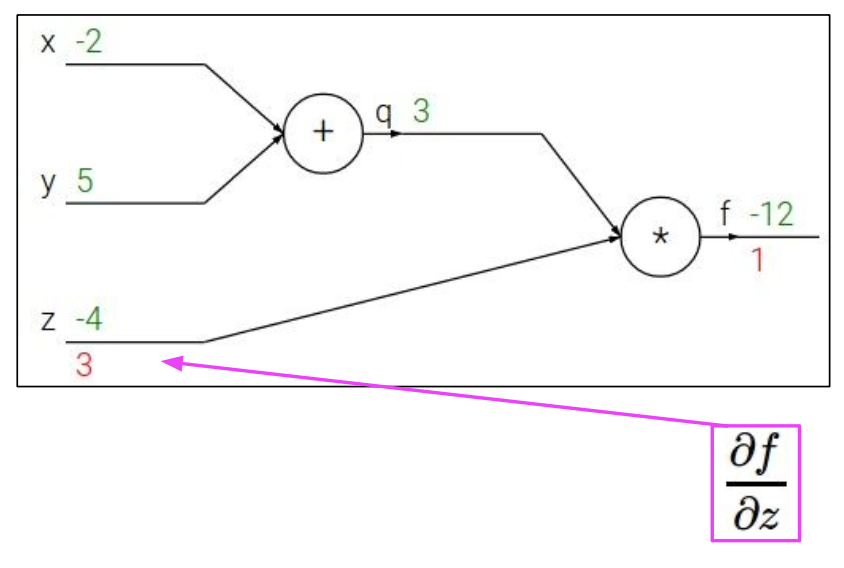
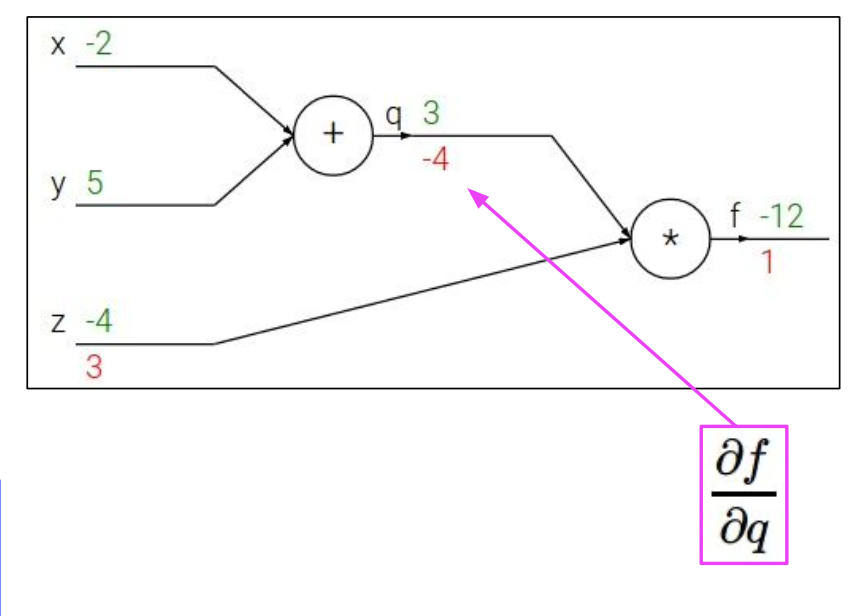
가 에 직접적으로 영향을 미치지 않으므로 미분식을 변경하여 나타냈다.
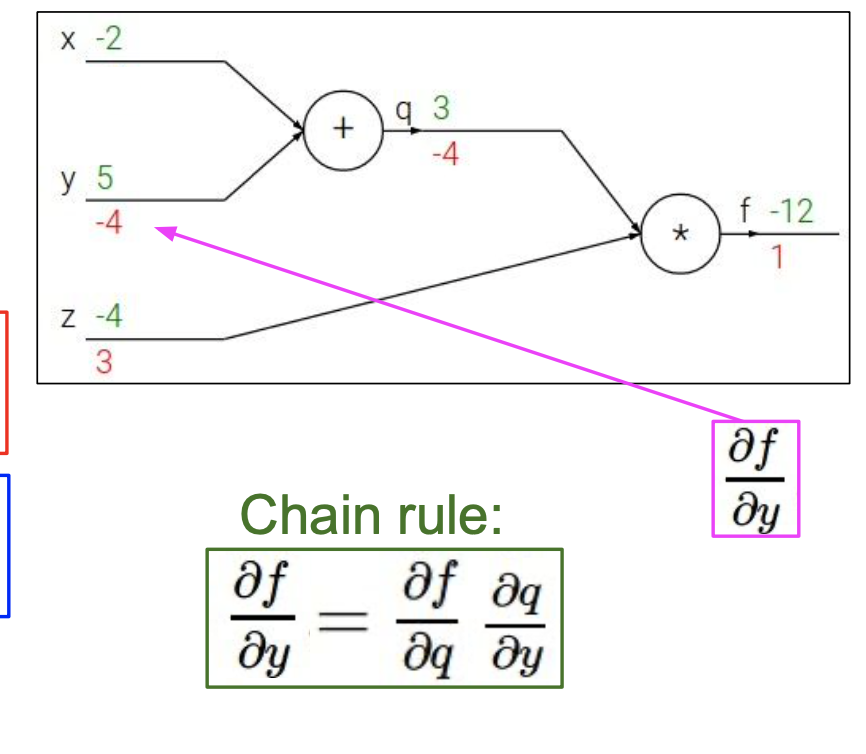
가 에 직접적으로 영향을 미치지 않으므로 미분식을 변경하여 나타냈다.
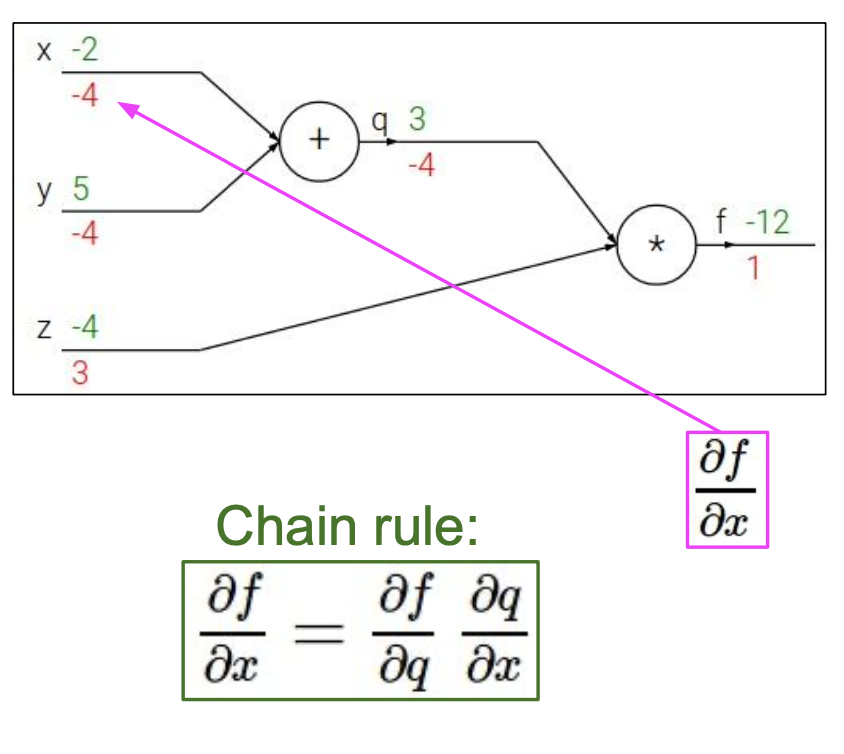
정리
Backpropagation sample example 2
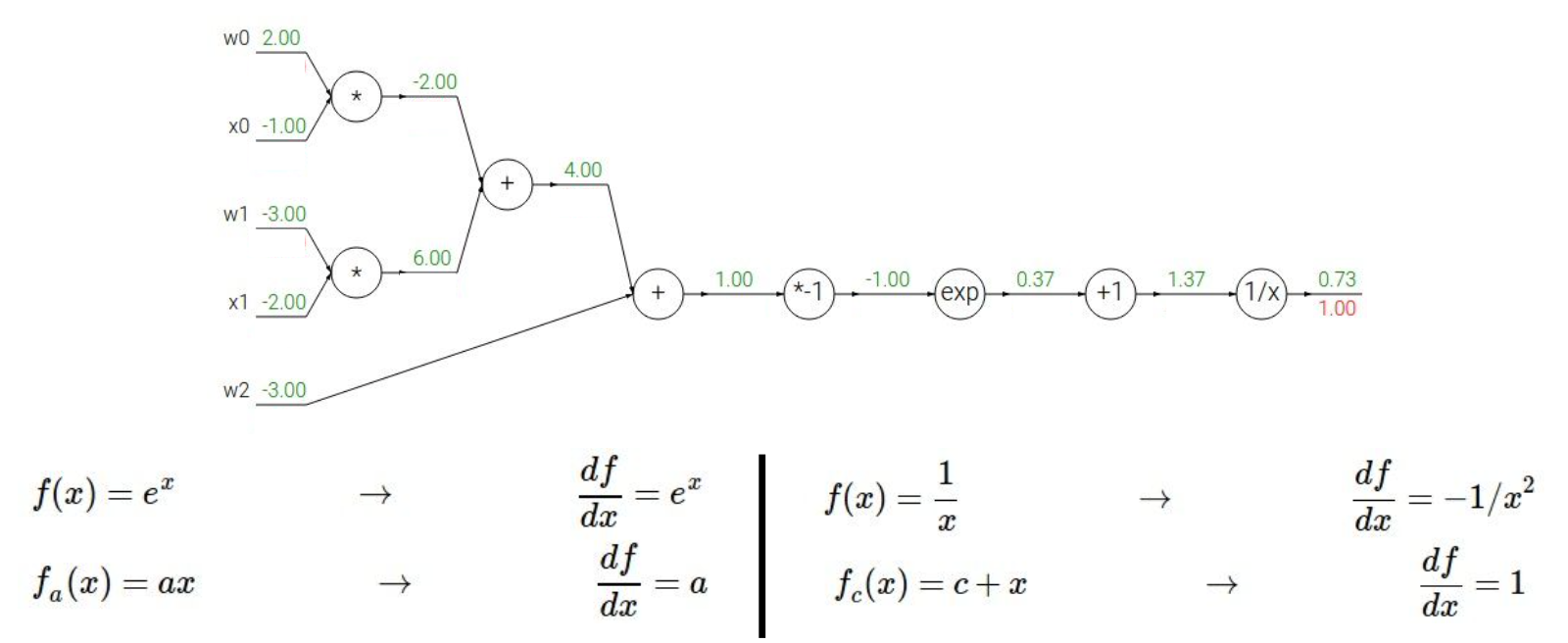
위 식에 sigmoid와 같은 함수를 씌울 수도 있다.
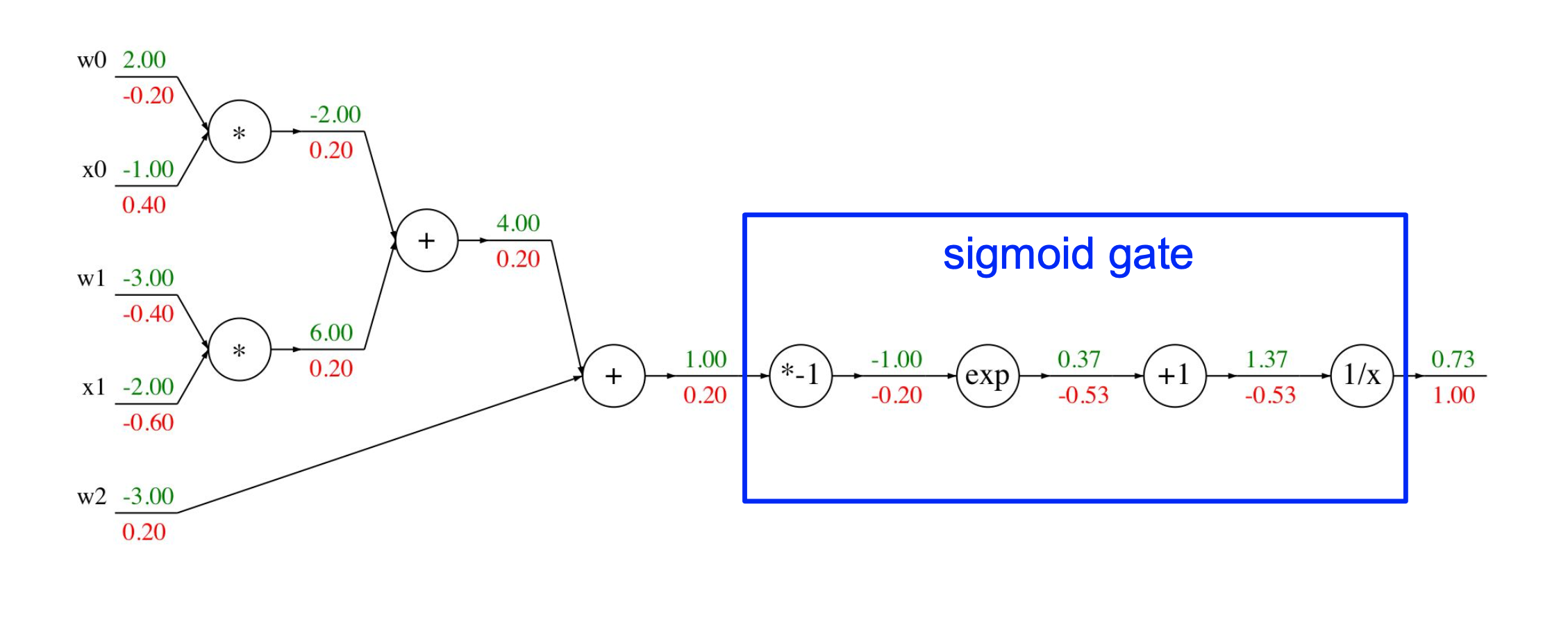
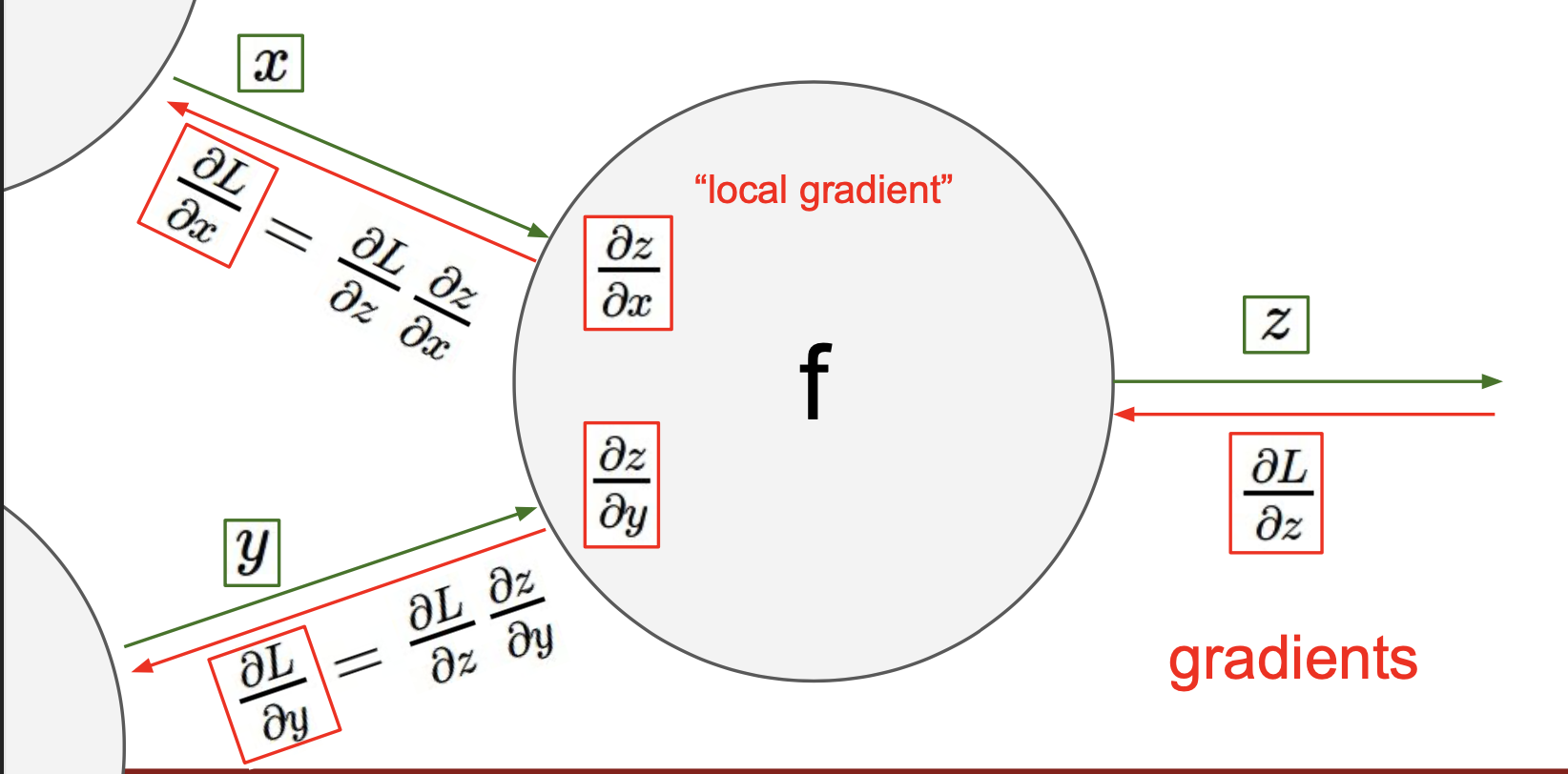
pattern in backward flow
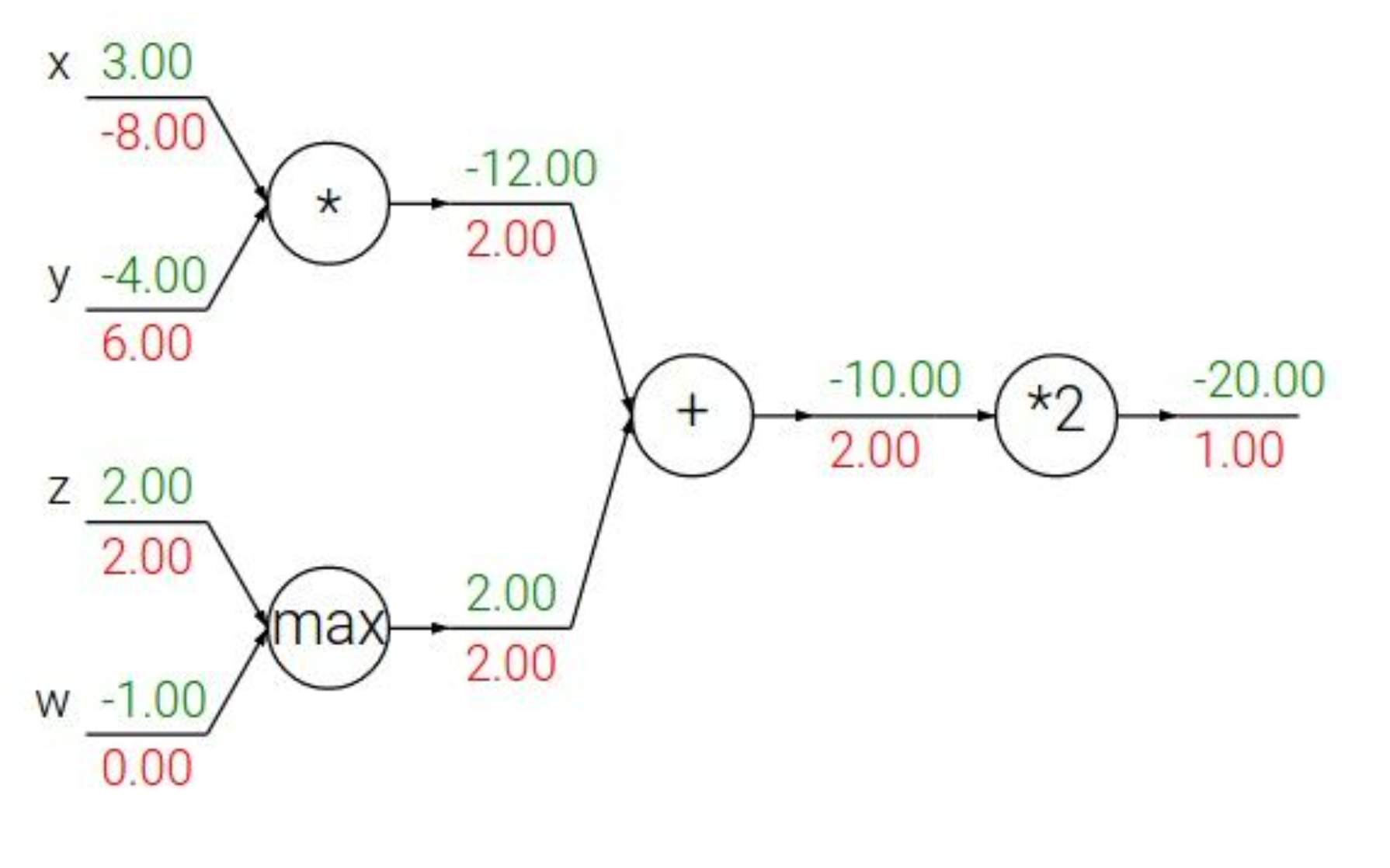
위 노드들의 연산들을 간략하게 정리해보면 아래와 같다.
- add : gradient distributor
- max : gradient router
- mul : gradient switcher
이번 포스팅은 scaler 일 때의 경우이고 다음 포스팅은 vector일 경우의 연산을 알아보겠다.