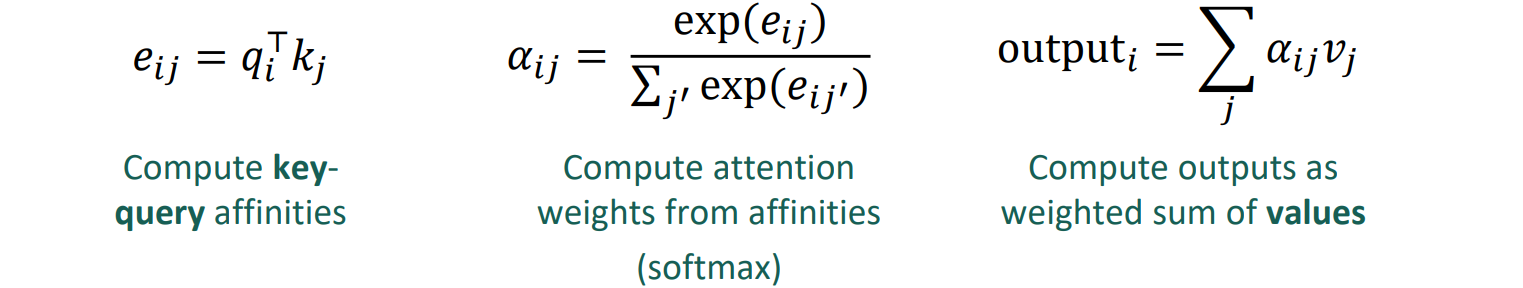Stanford CS224N NLP with Deep Learning | Winter 2021 | Lecture 9 - Self- Attention and Transformers
Circa 2016, nlp strategy
- bidirectional LSTM으로 문장 encoding
- LSTM decoder
- attention을 이용해 메모리에 유연하게 접근
- 2021년, 모델에서 최적의 building block은 무엇일까
RNN의 문제
Linear interaction distance
- gradient vanishing으로 long-distance dependencies를 학습하기 어렵다
- 선형 인접성을 인코딩하는데 linear order isn't the right way to think about sentences
Lack of parallelizability
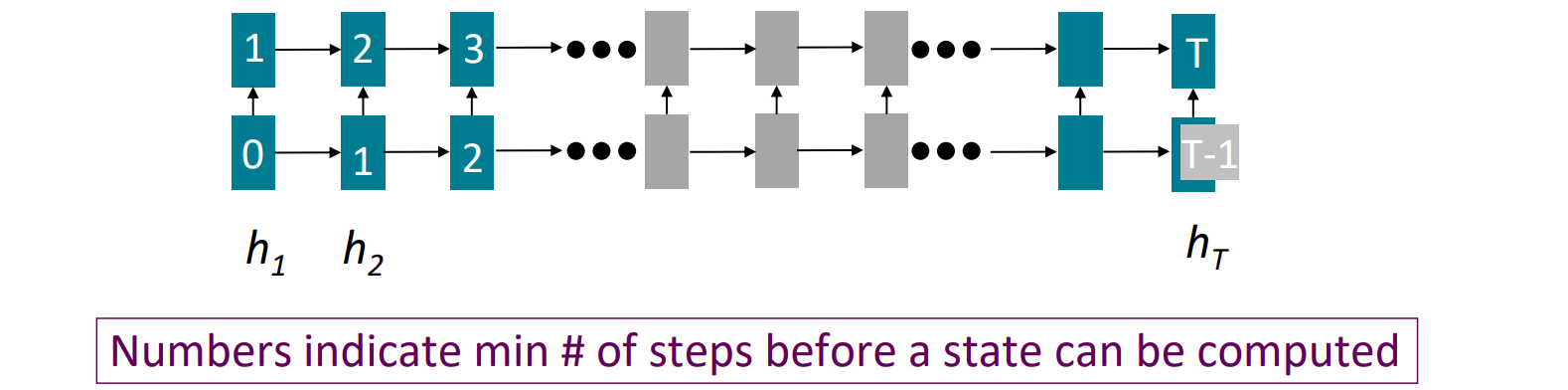
- 앞에 거 계산해야 뒤에 거 계산할 수 있다 → GPU 병렬 계산 활용 불가
Self-Attention
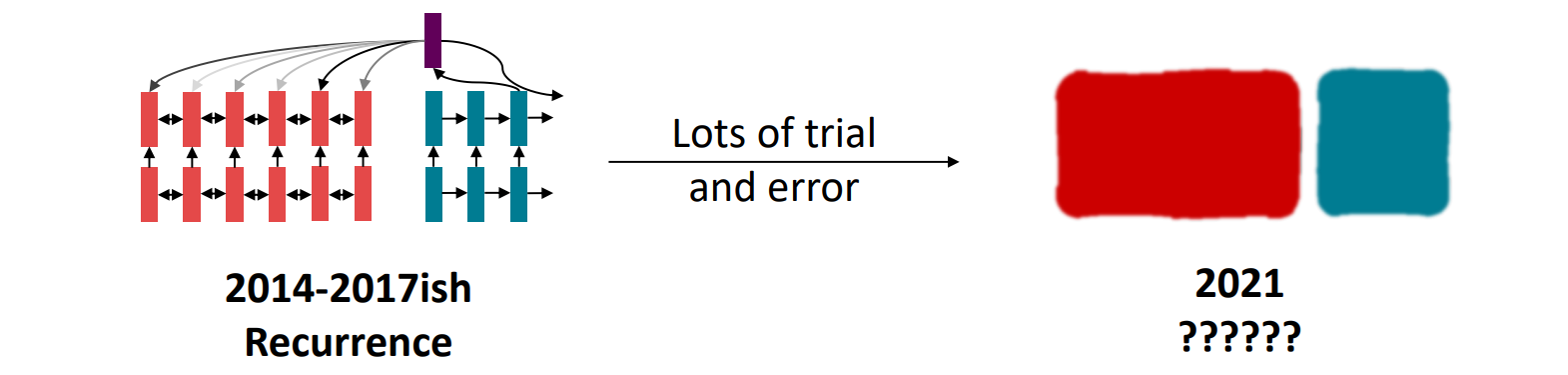
- queries q1,q2,...,qT / qi∈Rd
- keys k1,k2,...,kT / ki∈Rd
- values v1,v2,...,vT / vi∈Rd
- keys, queries, values는 같은 source에서 생성된다
만약 이전 층의 출력이 x1,x2,...,xT(단어 당 벡터 하나) 라면, vi=ki=qi=xi로 모두 같은 벡터
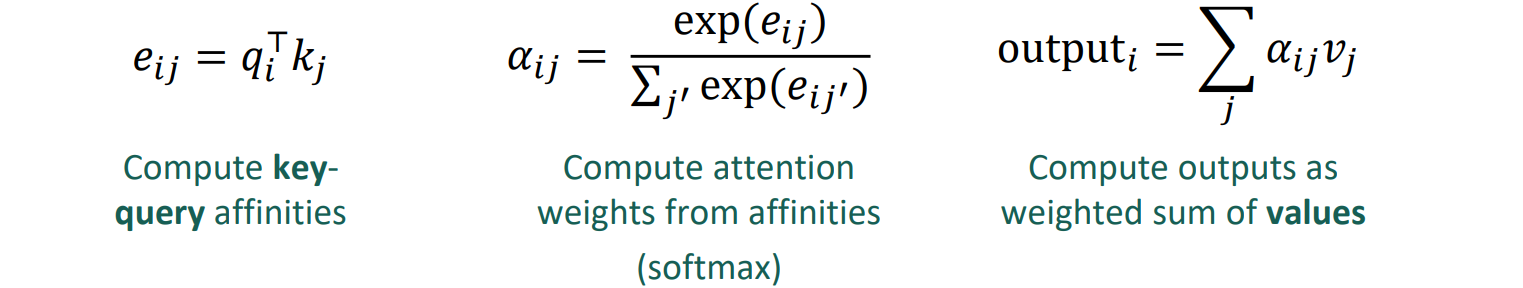
Self-Attention as an NLP building block
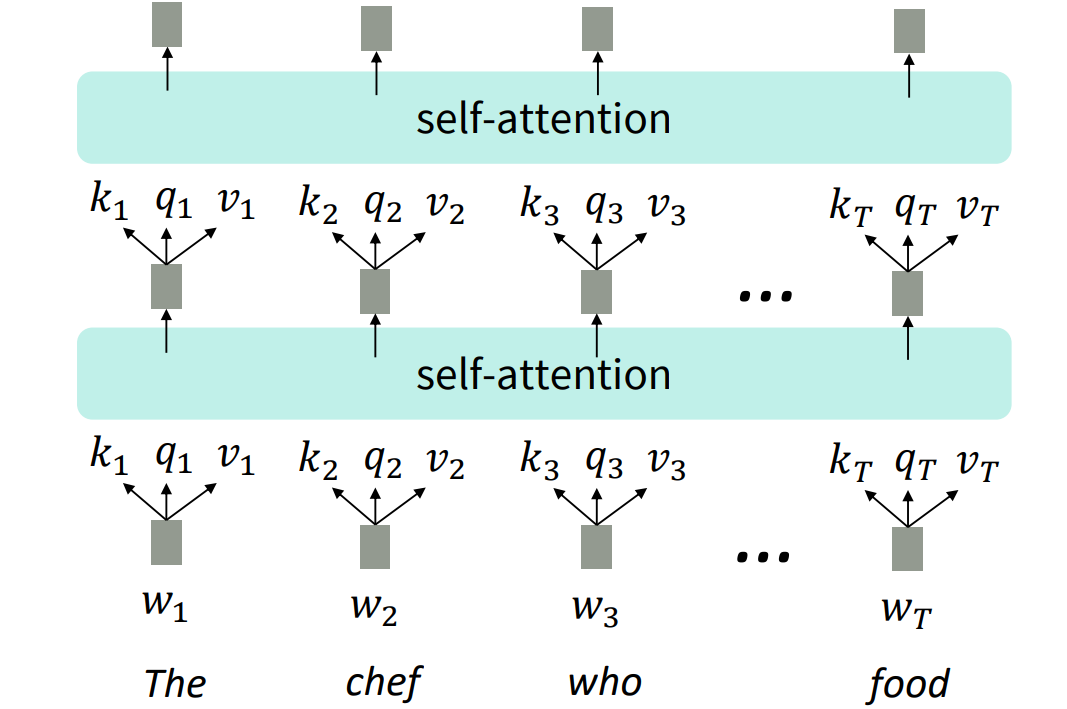
- LSTM을 쌓았던 것과 같이 Self-Attention block을 쌓았다
- Self-Attention은 집합으로 연산되기 때문에 순서에 대한 정보가 누락되어 있다
- 위치벡터의 필요성 제시
position vector
- pi∈Rd,i∈{1,2,...,T}
- ki=ki~+pi
qi=qi~+pi
vi=vi~+pi
- Sinusoidal position representations: concatenate sinusoidal functions of varying periods
- Learned absolute position representation: 모든 pi를 학습가능한 매개변수로 놓자
Adding nonlinearities
- add a feed-forward network to each output vector
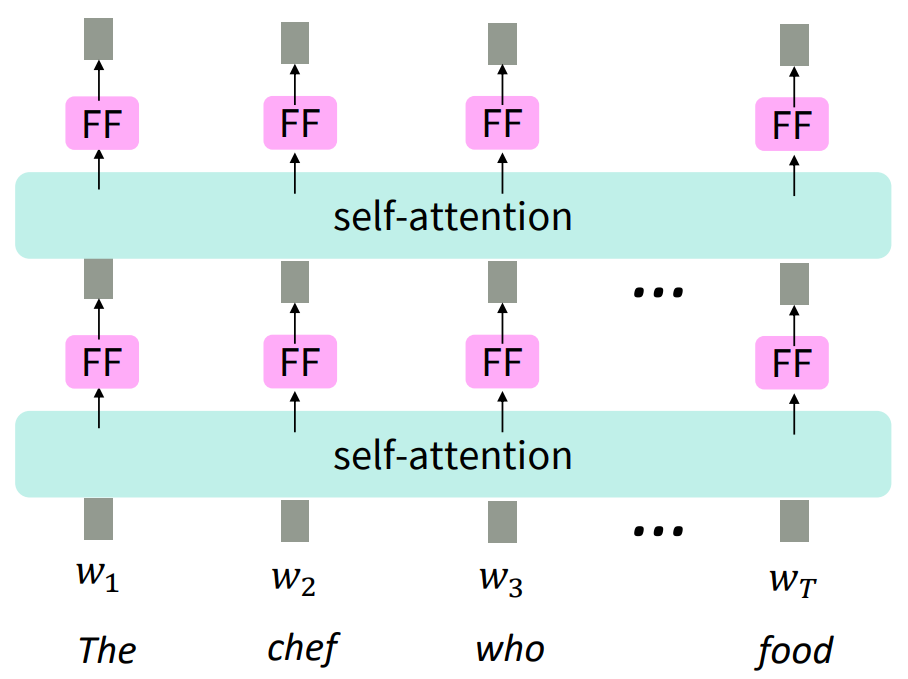
Masking the future
- mask out attention to future words by setting attention scores to −∞
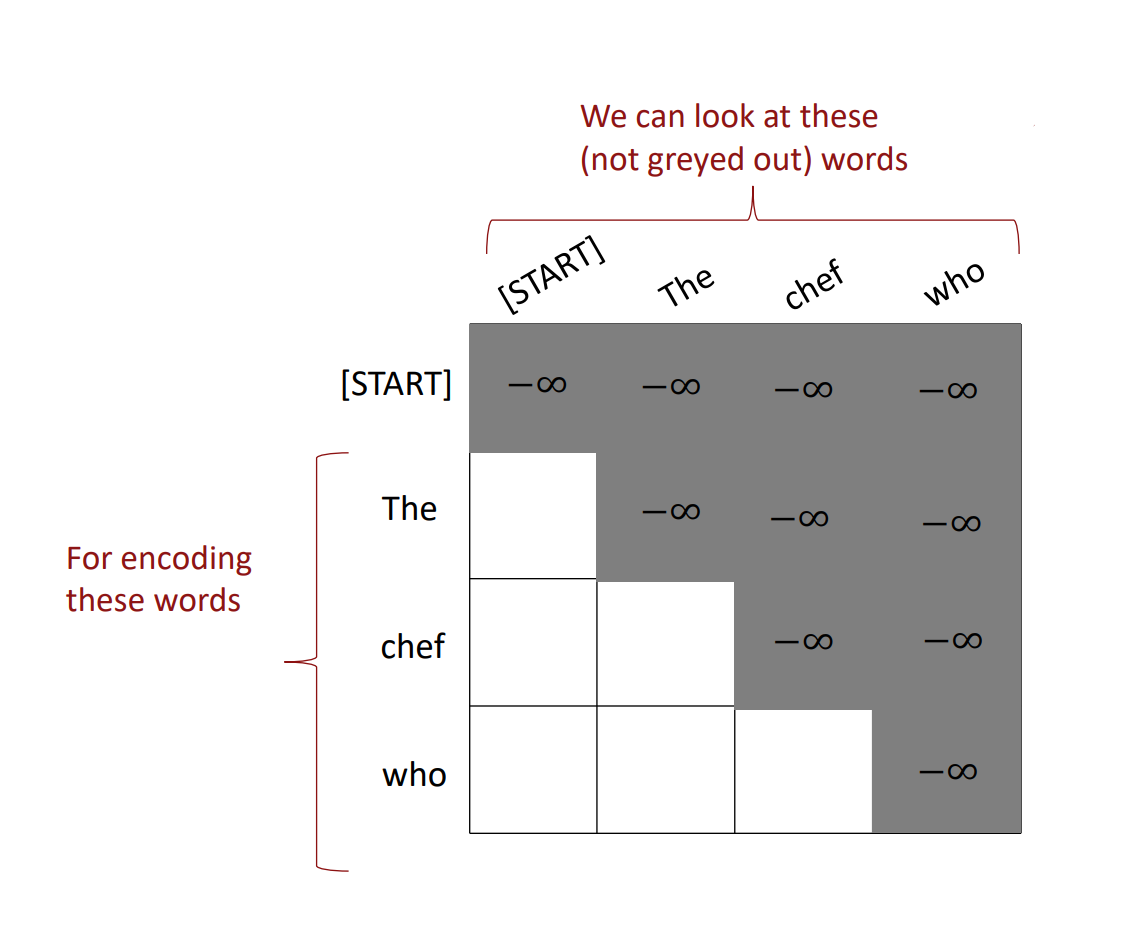
- concatenation of input vectors X=[x1,...,xT]∈RT×d
- key matrix ki=Kxi / K∈Rd×d
- query matrix qi=Qxi / Q∈Rd×d
- value matrix vi=Vxi / V∈Rd×d
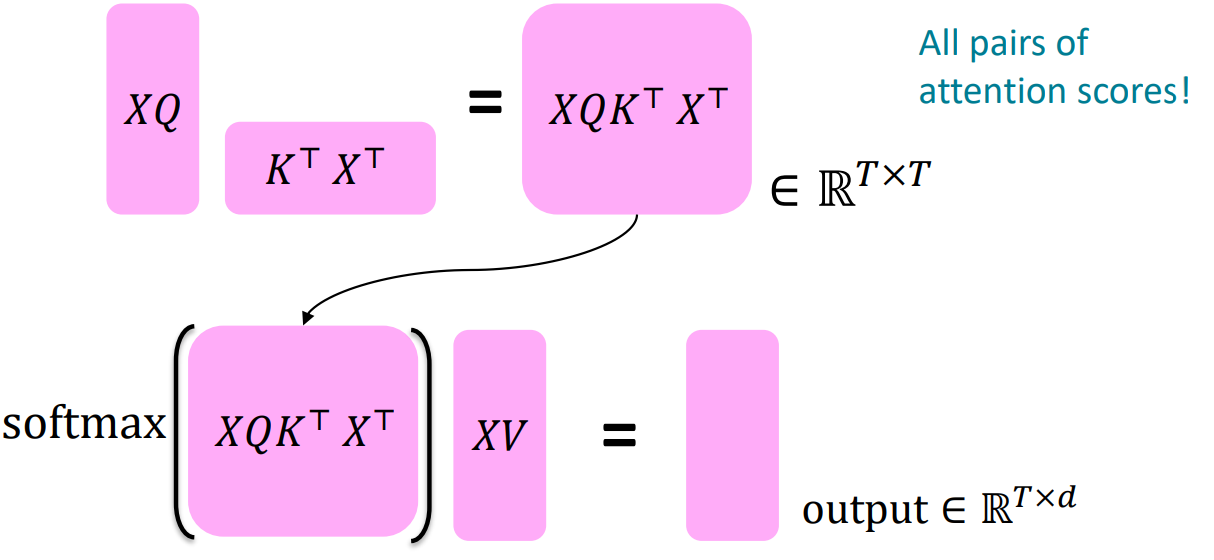
- XK∈RT×d,XQ∈RT×d,XV∈RT×d
- output = softmax(XQ(XK)T)×XV
- key, query로 softmax 구해서 value랑 weigthed sum
- 문장 내 여러 곳을 동시에 보려면
- outputl=softmax(XQlKlTXT)∗XVl / outputl∈Rhd
- output=Y[output1,..,outputh] / Y∈Rd×d
- 각 head는 각기 다른 것에 집중하며 서로 다른 벡터 생성

- X^{(i)} = X^{(i-1)}+\texttt{Layer}(X^{(i-1)})
- layer i가 layer i−1과 어떻게 달라야 하는지만 학습
- gradient vanishing problem 완화
- hidden vector의 불필요한 정보 변동을 표준화를 통해 제거
- output=σ+ϵx−μ∗γ+β
- 차원 d가 증가하면 내적인 attention score 역시 커짐
- score가 커지면 softmax의 일부 값이 굉장히 커지게 되고 낮은 확률을 지니고 있던 값들도 너무 작아져 기울기가 0으로 수렴하는 문제 발생
- attention score을 d/h로 나누어준다
outputl=softmax(d/hXQlKlTXT)∗XVl,outputl∈Rhd
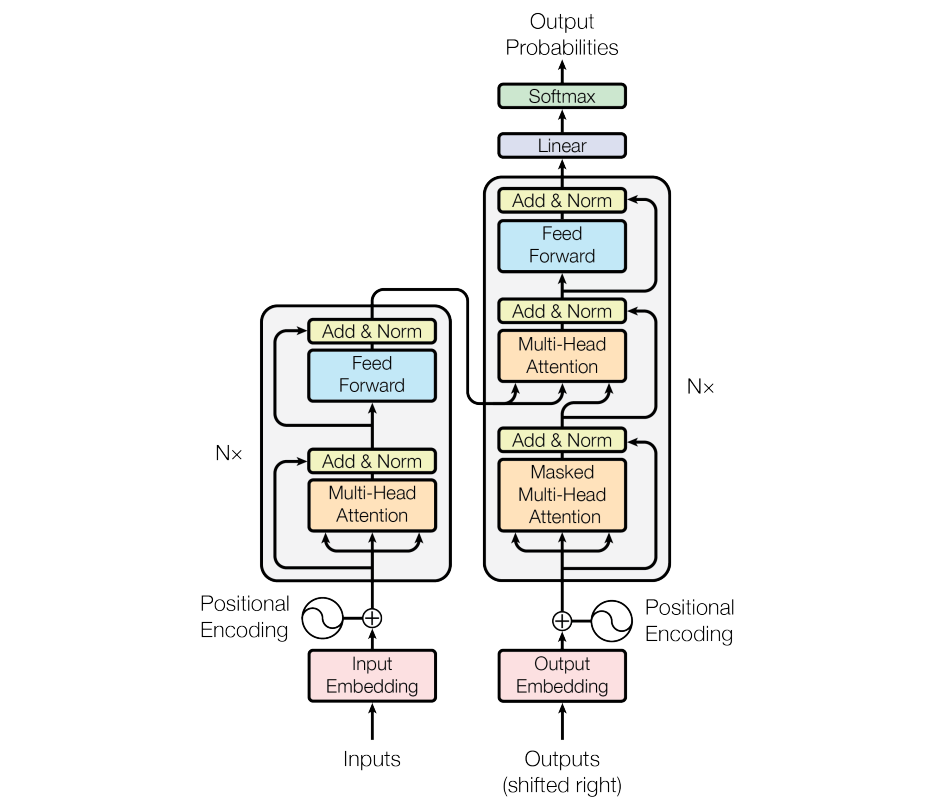
- 매 층마다 residual과 layer normalization 수행
- feed forward는 attention 연산이 완료된 후에 적용
- encoder는 단순 multi-head attention
- decoder는 미래를 추론해야 하기 때문에 masked multi-head attention
- cross-attention: encoder의 출력값과 decoder의 출력값 합쳐서 attention 수행
- encoder vectors H=[hi,...,hT]∈RT×d
- decoder vectors Z=[zi,...,zT]∈RT×d
- keys와 values는 encoder로부터
ki=Khi,vi=Vhi
- quries는 decoder로부터
qi=Qzi
- output=softmax(ZQ(HK)T)×HV