항상 기억하도록

• 해당 방법은 변수 x : 범주형이며 // 변수 y : 숫자형인 경우에 대해서다.

1. 시각화 : sns.barplot()

• barplot
  - 그래프를 통해 평균값의 차이와 신뢰구간의 차이를 확인한다.

ex)
sns.barplot(x="Survived", y="Age", data=titanic)
plt.grid()
plt.show()

• 해당 그래프에서 각 범주의 y 값은 평균 값을 나타낸다.
• 가운데 위에 있는 직선은 각 범주의 신뢰구간(95%) = 오차범위를 나타낸다.
• 1) 두 평균에 차이가 크고, 2) 신뢰구간(위에직선)이 겹치지 않을 때, 대립가설이 맞다고 볼 수 있다.

2. 수치화 : t-test // ANOVA

• null 값이 있으면 안됨

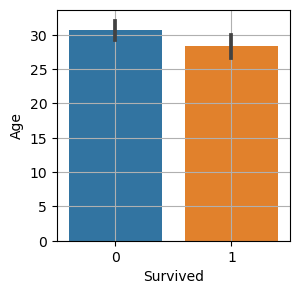
• t-test
  - x 범주가 2개일 경우 사용하며, 각 범주의 평균 값 차이를 비교한다.
  • t 통계량의 절대값이 2보다 큰 경우, 차이가 있다고 판단한다.
  • p-value < 0.05인 경우 차이가 있다고 판단한다.
  • t 통계량은 두 평균의 차이를 표준오차로 나눈 값

#1 데이터 준비(결측치 확인)
titanic['Age'].value_counts(dropna=False)
temp = titanic.loc[titanic['Age'].notnull()]

#2 각 범주 별 y 값으로 데이터 저장
died = temp.loc[temp['Survived']==0, 'Age']
survived = temp.loc[temp['Survived']==1, 'Age']    

#3 t-test
spst.ttest_ind(died, survived)
<출력>
Ttest_indResult(statistic=2.06668694625381, pvalue=0.03912465401348249)

• ANOVA
  - x 범주가 3개이상일 경우 사용하며, 전체 평균과 각 범주의 평균 값을 비교한다.
  • f 통계량의 값이 대략 3이상인 경우, 차이가 있다고 판단한다.
  • p-value < 0.05인 경우 차이가 있다고 판단한다.
  • f 통계량 = 집단 간 분산 / 집단 내 분산
  • 분산 : 평균과 개별 값의 차이

#1 데이터 준비, 그룹 별 데이터 저장
temp = titanic.loc[titanic['Age'].notnull()]

P_1 = temp.loc[temp.Pclass == 1, 'Age']
P_2 = temp.loc[temp.Pclass == 2, 'Age']
P_3 = temp.loc[temp.Pclass == 3, 'Age']

#2 ANOVA
spst.f_oneway(P_1, P_2, P_3)
<출력>
F_onewayResult(statistic=57.443484340676214, pvalue=7.487984171959904e-24)