2023. 05. 18.
벨만-포드 (Bellman-ford-moore) 📌
벨만-포드 알고리즘은 그래프에서 최단 거리를 구하는 알고리즘으로, 특정 출발 노드에서 다른 모든 노드까지의 최단 경로를 탐색한다. 다익스트라 알고리즘과 다른 점은 음수 가중치 에지가 있어도 수행할 수 있다는 것이다. 또한 전체 그래프에서 음수 사이클의 존재 여부를 판단할 수 있다.
시간복잡도: O(VE) V(노드 수) E(에지 수)
벨만-포드의 핵심 이론
📢 벨만-포드의 원리
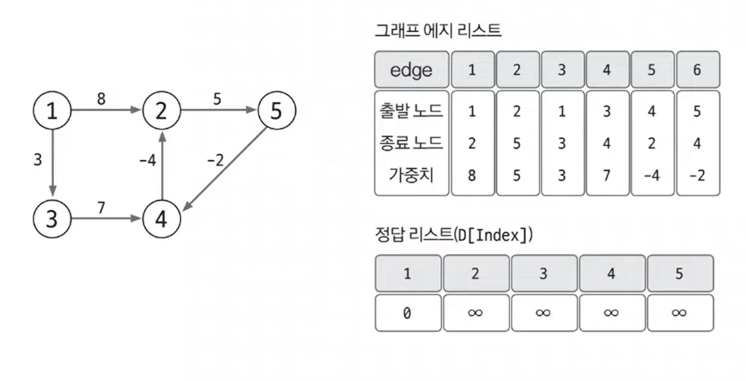
- 벨만-포드 알고리즘은 에지를 중심으로 동작하므로 그래프를 에지 리스트로 구현한다. 또한 최단 경로 리스트를 출발 노드는 0, 나머지 노드는 무한대로 초기화한다.
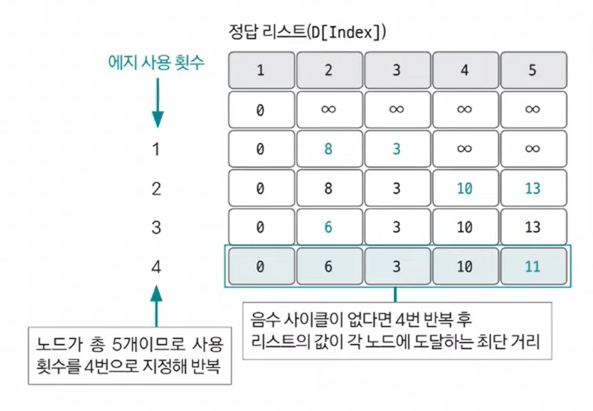
- 최단 거리 리스트에서 업데이트 반복 횟수는 노드 개수 - 1이다. 노드 개수가 N이고, 음수 사이클이 없을 때 특정 두 노드의 최단 거리를 구성할 수 있는 에지의 최대 개수는 N-1이기 때문이다. 업데이트 반복 횟수가 K번이라면 해당 시점에 정답 리스트의 값은 시작점에서 K개의 에지를 사용했을 때 각 노드에 대한 최단 거리이다.
업데이트 조건과 방법
D[s]가 무한대가 아니며 D[e](종료하고 있는 최단경로 리스트 값) > D[s](시작하는 최단경로 리스트 값) + w(가중치)일 때 D[e] = D[s] + w로 리스트의 값을 업데이트한다.
- 처음 제시한 사진에서 방향 그래프를 보면 노드 1에서 노드 2로 가는 가중치의 값은 2이다. 위 업데이트 조건을 통해 확인해보면 출발 노드인 D[1]의 값은 무한대가 아니고 D[2] > D[1] + w가 성립하므로 D[2]를 D[1] + w로 업데이트 하는 것이다. 쉽게 말해 에지 사용 횟수에 맞는 에지를 사용했을 때 시작점에서 다른 노드까지의 최단거리를 구하는 것이다.
- 음수 사이클이 없을 때 N-1번 에지 사용 횟수를 반복하면 출발 노드와 모든 노드 간의 최단 거리를 알려주는 정답 리스트가 완성되지만 완성 후 마지막으로 그래프에 음수 사이클이 존재하는지 확인해야 한다.
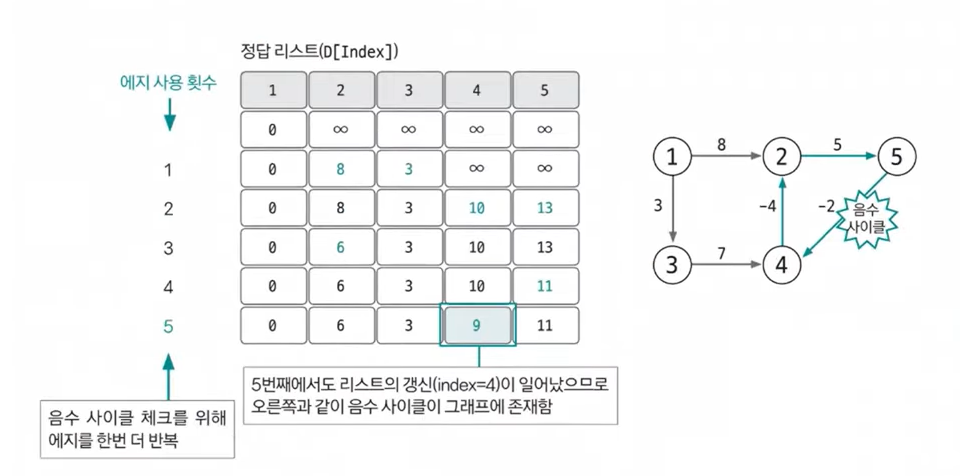
음수 사이클 유무 확인하는 방법
N-1번 돌렸을 때보다 한 번 더 돌렸을 때인 N번 돌렸을 때 가중치가 더 작아진다면 음수 사이클이 존재한다는 것이다. 음수 사이클이 존재하면 이 사이클을 무한하게 돌수록 가중치가 계속 감소하므로 최단 거리를 구할 수 없다. 아래 그래프에서 D[4] = 10이고 D[5] = 11이다. D[5] + w < D[4]이므로 D[4]의 값이 업데이트 된다. 그러므로 벨만-포드 알고리즘을 사용할 때는 N-1번의 에지로 업데이트를 통해서 최단거리를 구할 수 있어야 하고 한 번 더 업데이트를 해서 업데이트가 이루어지면 안되는 것이다.
2023. 05. 18. 오늘의 문제풀이 ✍
BOJ 2252 - 타임머신
import sys
INF = sys.maxsize
input = sys.stdin.readline
n,m = map(int,input().split())
edges = []
distance = [INF] * (n+1)
for _ in range(m):
s,e,cost = map(int,input().split())
edges.append((s,e,cost))
# 시작점 거리 0으로 초기화
distance[1] = 0
# 시작점이 무한대가 아니고 D[e] > D[s] + w일 경우에 업데이트
for _ in range(n-1):
for s,e,cost in edges:
if distance[s] != INF and distance[e] > distance[s] + cost:
distance[e] = distance[s] + cost
# 음수 사이클 확인
Minus_Cycle = False
for s,e,cost in edges:
if distance[s] != INF and distance[e] > distance[s] + cost:
Minus_Cycle = True
if Minus_Cycle:
print(-1)
else:
for i in range(2, n+1):
if distance[i] == INF:
print(-1)
else:
print(distance[i])출처
Do it algorithm