2023. 05. 15.
위상정렬 📌
위상정렬은 사이클이 없는 방향 그래프 (Directed Acyclic Graph - DAG)에서 노드 순서를 찾는 알고리즘으로 항상 유일한 값으로 정렬되지 않는다. 또한 사이클이 존재하면 노드 간의 순서를 명확하게 정의할 수 없으므로 위상 정렬을 적용할 수 없다.
위상정렬의 핵심 이론
📢 위상정렬의 원리
진입 차수
1. 진입 차수는 자기 자신을 가리키는 에지의 개수이다. 아래 사진과 같이 사이클이 없는 그래프를 이차원 리스트로 표현하였다.
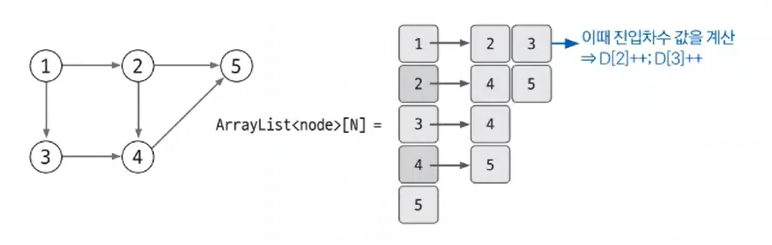
위 사진을 보면 노드 1을 가리키고 있는 에지가 없으므로 D[0]의 값은 0이 될 것이고 노드 2와 노드 3이 4를 가리키고 있으므로 D[4]의 값은 2가 된다.

2. 진입 차수 리스트에서 진입 차수가 0인 노드를 선택하고 선택된 노드를 정렬 리스트에 저장한다. 그 후 인접 리스트에서 선택된 노드가 가리키는 노드들의 진입 차수를 하나씩 뺀다. 위 사진을 예시로 보면 진입 차수 배열의 값이 0인 건 노드 1밖에 없다. 노드 1을 위상 정렬 리스트에 저장하고 그 후 인접 리스트에서 선택된 노드가 가리키는 노드들의 진입 차수를 1씩 뺀다. 다시 말해 정렬 리스트에 노드 1을 저장하고 노드 1이 가리키는 노드 2와 노드 3의 진입 차수를 1씩 빼는 것이다.
2023. 05. 15. 오늘의 문제풀이 ✍
BOJ 2252 - 줄 세우기
위 문제를 보고 바로 위상정렬을 사용하겠다는 생각이 들기 쉽지 않지만 출력 부분에서 "답이 여러 가지인 경우에는 아무거나 출력한다"라는 말을 보고 결과값이 항상 유일하지 않은 알고리즘인 위상정렬을 의심해볼 수 있다.
import sys
from collections import deque
input = sys.stdin.readline
n,m = map(int,input().split())
data = [[] for _ in range(n+1)] # 인접리스트
indegree = [0] * (n+1) # 진입차수 리스트
for _ in range(m):
s,e = map(int,input().split())
data[s].append(e) # 학생 A가 학생 B의 앞에 서야하므로
indegree[e] += 1
queue = deque()
for j in range(1, n+1):
if indegree[j] == 0:
queue.append(j)
while queue:
now = queue.popleft()
print(now, end = ' ')
for i in data[now]:
indegree[i] -= 1
if indegree[i] == 0:
queue.append(i)
출처
Do it algorithm
