Node 10. Finance Time Series 데이터 활용하기

10-1. 들어가며

---

학습 목표

• Data Labeling 방식에 대한 학습
• 예측값에 대한 설명력 높은 Feature 선정하는 방식에 대한 학습
• 분류기 성능 개선 방안에 대한 학습

10-2. Data Labeling

---

1. 추세 판단 분류기

금융 분야에서의 추세(Trend)?

• 주가 또는 코인 가격이 일정 방향으로 ➡️ 상승 or 하락 or 꾸준히 유지
• 보합: 상승 or 하락 어떠한 방향으로도 움직이지 않고 정체(=추세가 아님)
• 모멘텀: 추세 판단을 위한 지표(상승 or 하락 추세 유지의 동력)
• 추세와 모멘텀은 거의 동치의 의미로 사용됨
• 즉, 추세 판단은 모멘텀 포착과 같은 의미

활용 데이터

• Upbit(국내 암호화폐 거래소)의 이더리움 분봉을 이용한 분류기 개발
  • 이더리움 : 2017-00-00 ~ 2019-00-00까지

분류기 개발 방안

• 지도학습 기반 분류기
• 상승 : 1, 하락 : 0으로 라벨링
• RF를 기반으로 배깅 분류기 만듦

Package Import & Data Loading

import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm
import warnings
warnings.filterwarnings('ignore')

DATA_PATH = '/aiffel/aiffel/fnguide/data/'
modify_data = pd.read_csv(os.path.join(DATA_PATH, 'sub_upbit_eth_min_tick.csv'), index_col=0, parse_dates=True)
modify_data.loc['2017-11-01':'2017-12-31','close'].plot()

2. Data Labeling

• 4가지 방법
  • Price Change Direction
  • Using Moving Average
  • Local Min-Max
  • Trend Scanning

Price Change Direction

• 현재 가격 및 특정 영업일 이전 가격 차이로 라벨링

• 간단하지만, 가격 비교 기준에 따라 변동폭이 커질 수 있기 때문에 주의 필요
  

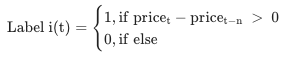
• 모멘텀 시그널 생성

window = 10
momentum_signal = np.sign(np.sign(modify_data['close'] - modify_data['close'].shift(window)) + 1)
s_momentum_signal = pd.Series(momentum_signal, index=modify_data.index)

• 특정 영업일 데이터 필터링

sub_data = modify_data.loc['2017-11-21', 'close']
c_sig = s_momentum_signal.loc['2017-11-21']
c_sig['color'] = np.where(c_sig == 1, 'red', 'blue')

plt.figure(figsize=(10,5))
plt.scatter(sub_data.index, sub_data, c=c_sig['color'])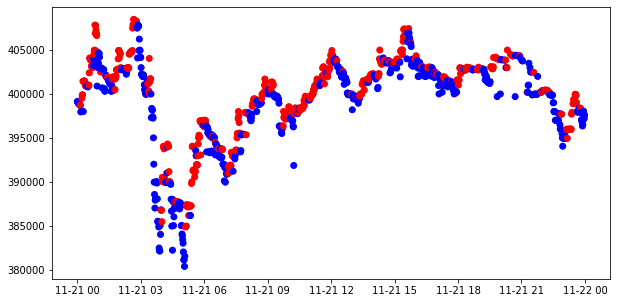

Using Moving Average

• 이동평균 이용

• 현재 주가가 특정 이동평균선 위 or 아래 위치 여부에 따라 라벨링

• 이 역시 간단하지만, 이동평균을 며칠로 할 것인지에 대한 결정 필요

• 이동 평균으로 인해 lag(지연) 발생
  

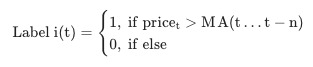
• .rolling(window).mean()) + 1

momentum_signal = np.sign(np.sign(modify_data['close'] - modify_data['close'].rolling(window).mean()) + 1)
s_momentum_signal = pd.Series(momentum_signal, index=modify_data.index)

sub_data = modify_data.loc['2017-11-21', 'close']
c_sig = s_momentum_signal.loc['2017-11-21']
c_sig['color'] = np.where(c_sig == 1, 'red', 'blue')

plt.figure(figsize=(10,5))
plt.scatter(sub_data.index, sub_data, c=c_sig['color'])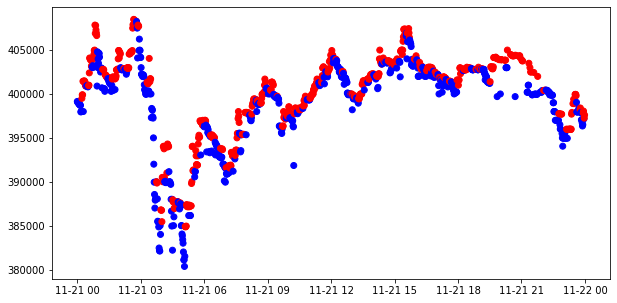

Local Min-Max

• 국지적 최소, 최댓값을 계속 갱신하는 방식으로 최소-최대 구간을 이어 라벨링
  • 현재 알고리즘) 지속적으로 최소, 최댓값을 갱신 -> 상대방 값으로 초기화
  • ex.하락 구간으로 인해 최솟값의 갱신이 이뤄지고 있는 상황
    • 최솟값 갱신에 이어 다음 가격에 상승이 시작되면 -> 하락구간 종료와 함께 최솟값 갱신 중단 -> 이전 최대값을 현재 최솟값으로 변경 -> 상승구간에서 최댓값 갱신이 되도록 조정!
  • 바로 하락 구간 종료를 하면 너무 자주 라벨링 변화가 일어나기 때문에, Wait 계수를 통해 조절
• 순차적이기 때문에 데이터 증가 ➡️ 선형적 연산 시간 증가(단점)
• Wait 계수가 너무 작을 경우, 변동성이 커지니 잘 선택해야 함

슈도 코드

𝐼𝑛𝑖𝑡𝑖𝑎𝑙𝑖𝑧𝑒 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠𝑓𝑜𝑟 𝑖 𝑖𝑛 𝑑𝑎𝑡𝑎𝑠𝑒𝑡:
    𝑖𝑓 𝑐𝑢𝑟𝑟𝑒𝑛𝑡𝑝𝑟𝑖𝑐𝑒<𝑝𝑟𝑒𝑣𝑖𝑜𝑢𝑠𝑚𝑖𝑛𝑝𝑟𝑖𝑐𝑒
        𝑚𝑖𝑛𝑝𝑟𝑖𝑐𝑒←𝑐𝑢𝑟𝑟𝑒𝑛𝑡𝑝𝑟𝑖𝑐𝑒
        𝑝𝑎𝑠𝑠𝑖𝑛𝑔 𝑡ℎ𝑟𝑜𝑢𝑔ℎ 𝑡ℎ𝑒 𝐹𝑎𝑙𝑙𝑖𝑛𝑔 𝑇𝑟𝑒𝑛𝑑
        𝑎𝑐𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑒𝑠𝑚𝑖𝑛𝑝𝑟𝑖𝑐𝑒
    𝑖𝑓 𝑐𝑢𝑟𝑟𝑒𝑛𝑡𝑝𝑟𝑖𝑐𝑒>𝑝𝑟𝑒𝑣𝑖𝑜𝑢𝑠𝑚𝑎𝑥𝑝𝑟𝑖𝑐𝑒
        𝑚𝑎𝑥𝑝𝑟𝑖𝑐𝑒←𝑐𝑢𝑟𝑟𝑒𝑛𝑡𝑝𝑟𝑖𝑐𝑒
        𝑝𝑎𝑠𝑠𝑖𝑛𝑔 𝑡ℎ𝑟𝑜𝑢𝑔ℎ 𝑡ℎ𝑒 𝑅𝑖𝑠𝑖𝑛𝑔 𝑇𝑟𝑒𝑛𝑑
        𝑎𝑐𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑒𝑠𝑚𝑎𝑥𝑝𝑟𝑖𝑐𝑒
    𝑖𝑓 𝑒𝑛𝑑𝑠 𝑡ℎ𝑒 𝐹𝑎𝑙𝑙𝑖𝑛𝑔 𝑇𝑟𝑒𝑛𝑑
        𝑚𝑎𝑥𝑝𝑟𝑖𝑐𝑒←𝑚𝑖𝑛𝑝𝑟𝑖𝑐𝑒
    𝑖𝑓 𝑒𝑛𝑑𝑠 𝑡ℎ𝑒 𝑅𝑖𝑠𝑖𝑛𝑔 𝑇𝑟𝑒𝑛𝑑
        𝑚𝑖𝑛𝑝𝑟𝑖𝑐𝑒←𝑚𝑎𝑥𝑝𝑟𝑖𝑐𝑒

• get_local_min_max 함수 정의

def get_local_min_max(close, wait=3):
    min_value = close.iloc[0]
    max_value = close.iloc[0]
    n_cnt_min, n_cnt_max = 0, 0
    
    mins, maxes = [], []
    min_idxes, max_idxes = [], []
    b_min_update, b_max_update = False, False
    
    for idx, val in zip(close.index[1:], close.values[1:]):
        if val < min_value:
            min_value = val
            mins.append(min_value)
            min_idxes.append(idx)
            n_cnt_min = 0
            b_min_update = True
        if val > max_value:
            max_value = val
            maxes.append(max_value)
            max_idxes.append(idx)
            n_cnt_max = 0
            b_max_update = True
        
        if not b_max_update:
            b_min_update = False
            n_cnt_min += 1
            if n_cnt_min >= wait:
                max_value = min_value
                n_cnt_min = 0
    
        if not b_min_update:
            b_max_update = False
            n_cnt_max += 1
            if n_cnt_max >= wait:
                min_value = max_value
                n_cnt_max = 0
               
    return pd.DataFrame.from_dict({'min_time': min_idxes, 'local_min': mins}), pd.DataFrame.from_dict({'max_time': max_idxes, 'local_max': maxes})

• Wait 계수 설정

mins, maxes = get_local_min_max(sub_data, wait=3)

• 결과 시각화
  • 최솟값 : blue
  • 최댓값 : red

fig, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.plot(sub_data, 'c')
ax.scatter(mins.min_time, mins.local_min, c='blue')
ax.scatter(maxes.max_time, maxes.local_max, c='red')
ax.set_ylim([sub_data.min() * 0.99, sub_data.max()  * 1.01])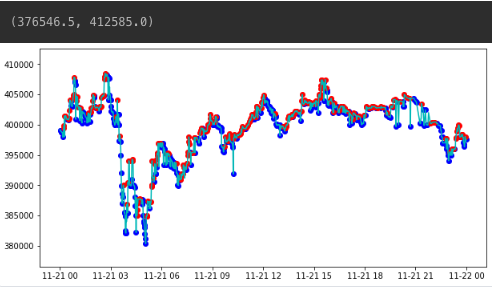

• 특정 시점으로 필터링하여 시각화

st_time, ed_time = '2017-11-21 09:00:00', '2017-11-21 16:00:00'

fig, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.plot(sub_data.loc[st_time:ed_time], 'c')
ax.scatter(mins.set_index('min_time', drop=False).min_time.loc[st_time:ed_time], mins.set_index('min_time').local_min.loc[st_time:ed_time], c='blue')
ax.scatter(maxes.set_index('max_time', drop=False).max_time.loc[st_time:ed_time], maxes.set_index('max_time').local_max.loc[st_time:ed_time], c='red')
ax.set_ylim([sub_data.min() * 0.99, sub_data.max()  * 1.01])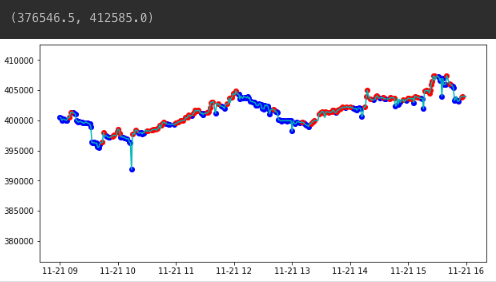

• 최솟값, 최댓값 개수 확인

mins.shape[0], maxes.shape[0]

Trend Scanning

• Machine Learning for Asset Managers에 소개된 라벨링 방식
• $x_t$(시계열 데이터) = 주식(코인) 가격
  • 현재 시점(t) ~ $t+l$ 시점의 회귀식 필터링을 통해 𝛽를 구하기
  • 𝛽값의 Tvalue 구하기
  • maxTvalue 부호를 통해 라벨링

• Tvalue?

  • 두 대상의 평균적 차이 정도를 표현(두 대상을 평균적으로 비교하고자)
  • t-value가 클수록 ➡️ 두 대상의 평균 차이가 커짐
  • ex. 나의 가설로 계산한 주가 vs 실제 주가의 평균적 차이
    • 가설 계산 주가 - 실제 주가 사이의 t-value가 0에서 멀다 ➡️ 두 주가 사이의 차이가 크다!

  

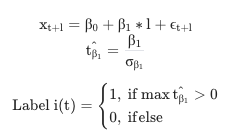
코드 참고 : Git MLFinLab

• 선형 추세의 t-value 값 계산

def t_val_lin_r(close):
    import statsmodels.api as sml
    
    # t-value from a linear trend
    x = np.ones((close.shape[0], 2))
    x[:, 1] = np.arange(close.shape[0])
    ols = sml.OLS(close, x).fit()
    return ols.tvalues[1]

• 조건 설정
  • look_forward_window : 현재 시점에서 특정 미래 시점까지의 관찰할 윈도우 크기
  • min_sample_length : 샘플 데이터 최소 길이
  • step : 슬라이딩 윈도우 이동 시의 간격
  • t1_array : 특정 기준 시점 결과값 저장
  • t_values_array : 각 윈도우의 t-value 저장

look_forward_window = 60
min_sample_length = 5
step = 1
t1_array = []
t_values_array = []

• 실제 t-value 계산 진행 및 최대 t-value 선정
  • 현재 시점(ind)부터 미래 look_forward_window까지의 샘플 데이터 추출
  • 회귀 분석을 통한 t-value를 이용한 추세 추정 진행

molecule = modify_data['2017-11-01':'2017-11-30'].index
label = pd.DataFrame(index=molecule, columns=['t1', 't_val', 'bin'])
tmp_out = []

for ind in tqdm(molecule):
    subset = modify_data.loc[ind:, 'close'].iloc[:look_forward_window] # sample 추출
    if look_forward_window > subset.shape[0]:
        continue
    
    tmp_subset = pd.Series(index=subset.index[min_sample_length-1:subset.shape[0]-1])
    tval = []

    for forward_window in np.arange(min_sample_length, subset.shape[0]):
        df = subset.iloc[:forward_window]
        tval.append(t_val_lin_r(df.values))
    
    tmp_subset.loc[tmp_subset.index] = np.array(tval)
    idx_max = tmp_subset.replace([-np.inf, np.inf, np.nan], 0).abs().idxmax()
    tmp_t_val = tmp_subset[idx_max]
    tmp_out.append([tmp_subset.index[-1], tmp_t_val, np.sign(tmp_t_val)])

label.loc[molecule] = np.array(tmp_out)  # prevent leakage

label['t1'] = pd.to_datetime(label['t1'])
label['bin'] = pd.to_numeric(label['bin'], downcast='signed')

• 2017년 11월 21일 종가 데이터 시각화

sub_data = modify_data.loc['2017-11-21', 'close']
c_sig = label['bin'].loc['2017-11-21']
c_sig['color'] = np.where(c_sig == 1, 'red', 'blue')

fig, ax = plt.subplots(1, 1, figsize=(10, 5))
ax.scatter(sub_data.index, sub_data.values,
              c=c_sig['color'])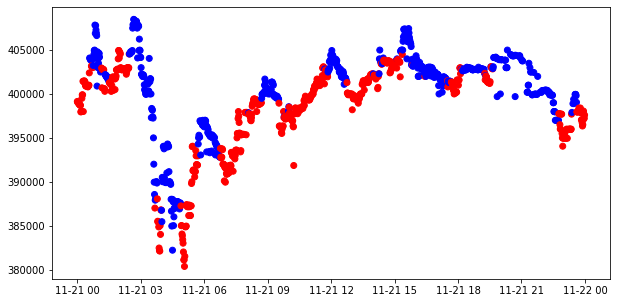

10-3. Feature Engineering

---

Feature 선택 방식 3가지

• Filter Method
  • 피쳐들 간 연관성을 찾는 방식
  • information gain, correlation coefficient, ...
• Wrapper Method
  • 해결하고자 하는 문제의 유용성 측정
  • Validation set에서의 성능 최대화 Feature Set 선정
  • Recursive Feature Elimination, Sequential Feature Selection, ...
• Embedded Method
  • 훈련 알고리즘 자체에 피쳐 선정 과정 포함
  • Lasso, Ridge, Elastic Net, ...

• Wrapper Method 사용법
• 주가 모멘텀 포착을 위한 사용 가능한 Feature 분석 및 선정 방식
• SHAP로 Feature importance 확인

환경 구성 및 데이터 불러오기

• ta, shap 설치

!pip install ta==0.9.0
!pip install shap

• 라이브러리 import

import datetime
import sys
import os
import re
import io
import json
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import ta

import sys
sys.path.append('/aiffel/aiffel/fnguide/data/')
from libs.feature_importance import importance as imp
from sklearn.feature_selection import SequentialFeatureSelector, RFECV

from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import KFold
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier, AdaBoostClassifier, VotingClassifier

• 데이터 불러오기

DATA_PATH = '/aiffel/aiffel/fnguide/data/'
anno_file_name = os.path.join(DATA_PATH, 'sub_upbit_eth_min_tick_label.pkl')
target_file_name = os.path.join(DATA_PATH, 'sub_upbit_eth_min_tick.csv')

df_modify_data = pd.read_csv(target_file_name, index_col=0, parse_dates=True)
df_label_data = pd.read_pickle(anno_file_name)
df_sub_modify_data = df_modify_data.loc[df_label_data.index]

# 1000개만 가져오기
df_sub_modify_data = df_sub_modify_data.iloc[:1000]

• df_sub_modify_data
  

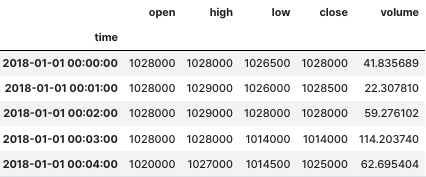
• df_label_data
  

• df_label_data.value_counts()
  

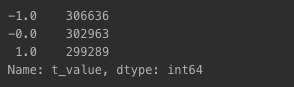
Technical Index

기술적 지표

• 시장 주가 or 거래량 데이터 기반 주가 향방 예측을 위한 지표

구분	설명	지표 종류
추세 지표	주가 방향성 포착 지표	MACD, ADX, TRIX, DPO, AROON...
변동성 지표	일정 기간 내 주가 변동폭 측정을 위한 지표	표준편차, ATR, UI...
거래량 지표	거래량 유입/유출 등 변화 측정	CMF, MFI, FI, SMA EM, VPT...
모멘텀 지표	현재 주가 상대적 강도 측정	RSI, WR...

• 추세 지표
  • MACD : 단기 이평선, 장기 이평선 차이로 주가 수렴/확산 정도를 나타냄
    • signal, average, diverence
  • ADX : 금일 주가 움직임 범위가 전일 범위 방향으로부터 어디로 벗어난건지 관찰, 추세 강도 추적
  • TRIX : n-영업일 지수가중평균의 3번 연속 수행 -> 기울기
  • DPO : 최신 가격 흐름에 심하게 변동되지 않도록 변위된 이동평균을 통해 장기 추세 제거
    • 중기 과매수/과매도 정도
  • AROON : 추세 강도 및 변화 식별
    • 고가 사이 시간차, 저가 사이 시간차 측정

• 변동성 지표
  • ATR : 시장 변동성 측정
    • 아래 3가지 중 큰 값을 통해 이동평균을 구함
      • 고가 - 저가
      • | 고가 - 전일 종가 | (절댓값)
      • | 저가 - 전일 종가 |
  • UI : 가격 하락 유지 기간, 깊이 -> 가격 하락 위험 측정

• 거래량 지표
  • CMF : MSD와 유사한 산출 방식
    • 두 accumulation/distribution line EMA 차이로 돈 유입/유출 파악
  • MFI : 가격 흐름, 거래량 조합으로 모멘텀 방향성 평가
  • FI : 가격 및 거래량을 통해 가격 움직임의 강도 측정
  • SMA EM : 가격 변동성 및 거래량으로 가격 흐름 용이성 측정, 가격 상승/하락 판단
  • VPT : 가격 변화 강도 및 방향 측정(수요 및 공급 균형 측정)

• 모멘텀 지표
  • RSI : 가격 흐름 상대 강도 측정(일정 기간 내 평균 수익 및 손실 강도를 비교하는 것)
  • WR : 과매도 및 과매수 측정
    • -100 ~ 0
    • 진입 및 청산 시점 포착 시 주로 사용

실제 지표 산출

• TA 패키지 사용

mt = 1
fillna = False
df_ = df_sub_modify_data.copy()
open, high, low, close, volume = 'open', 'high', 'low', 'close', 'volume'
cols = [open, high, low, close, volume]

## Volume Index
# Chaikin Money Flow
df_["volume_cmf"] = ta.volume.ChaikinMoneyFlowIndicator(
                        high=df_[high], low=df_[low], close=df_[close], volume=df_[volume], window=20*mt, fillna=fillna
                    ).chaikin_money_flow()
# Force Index
df_["volume_fi"] = ta.volume.ForceIndexIndicator(
                        close=df_[close], volume=df_[volume], window=15*mt, fillna=fillna
                    ).force_index()
# Money Flow Indicator
df_["volume_mfi"] = ta.volume.MFIIndicator(
                        high=df_[high],
                        low=df_[low],
                        close=df_[close],
                        volume=df_[volume],
                        window=15*mt,
                        fillna=fillna,
                    ).money_flow_index()
# Ease of Movement
df_["volume_sma_em"] = ta.volume.EaseOfMovementIndicator(
                            high=df_[high], low=df_[low], volume=df_[volume], window=15*mt, fillna=fillna
                        ).sma_ease_of_movement()

# Volume Price Trend
df_["volume_vpt"] = ta.volume.VolumePriceTrendIndicator(
                        close=df_[close], volume=df_[volume], fillna=fillna
                    ).volume_price_trend()

## volatility index
# Average True Range
df_["volatility_atr"] = ta.volatility.AverageTrueRange(
                            close=df_[close], high=df_[high], low=df_[low], window=10*mt, fillna=fillna
                        ).average_true_range()

# Ulcer Index
df_["volatility_ui"] = ta.volatility.UlcerIndex(
                            close=df_[close], window=15*mt, fillna=fillna
                        ).ulcer_index()

## trend index
# MACD
df_["trend_macd_diff"] = ta.trend.MACD(
                            close=df_[close], window_slow=25*mt, window_fast=10*mt, window_sign=9, fillna=fillna
                        ).macd_diff()

# Average Directional Movement Index (ADX)
df_["trend_adx"] = ta.trend.ADXIndicator(
                        high=df_[high], low=df_[low], close=df_[close], window=15*mt, fillna=fillna
                    ).adx()

# TRIX Indicator
df_["trend_trix"] = ta.trend.TRIXIndicator(
                        close=df_[close], window=15*mt, fillna=fillna
                    ).trix()

# Mass Index
df_["trend_mass_index"] = ta.trend.MassIndex(
                            high=df_[high], low=df_[low], window_fast=10*mt, window_slow=25*mt, fillna=fillna
                        ).mass_index()

# DPO Indicator
df_["trend_dpo"] = ta.trend.DPOIndicator(
                        close=df_[close], window=20*mt, fillna=fillna
                    ).dpo()

# Aroon Indicator
df_["trend_aroon_ind"] = ta.trend.AroonIndicator(close=df_[close], window=20, fillna=fillna).aroon_indicator()

## momentum index
# Relative Strength Index (RSI)
df_["momentum_rsi"] = ta.momentum.RSIIndicator(close=df_[close], window=15*mt, fillna=fillna).rsi()

# Williams R Indicator
df_["momentum_wr"] = ta.momentum.WilliamsRIndicator(
                        high=df_[high], low=df_[low], close=df_[close], lbp=15*mt, fillna=fillna
                    ).williams_r()


# result
df_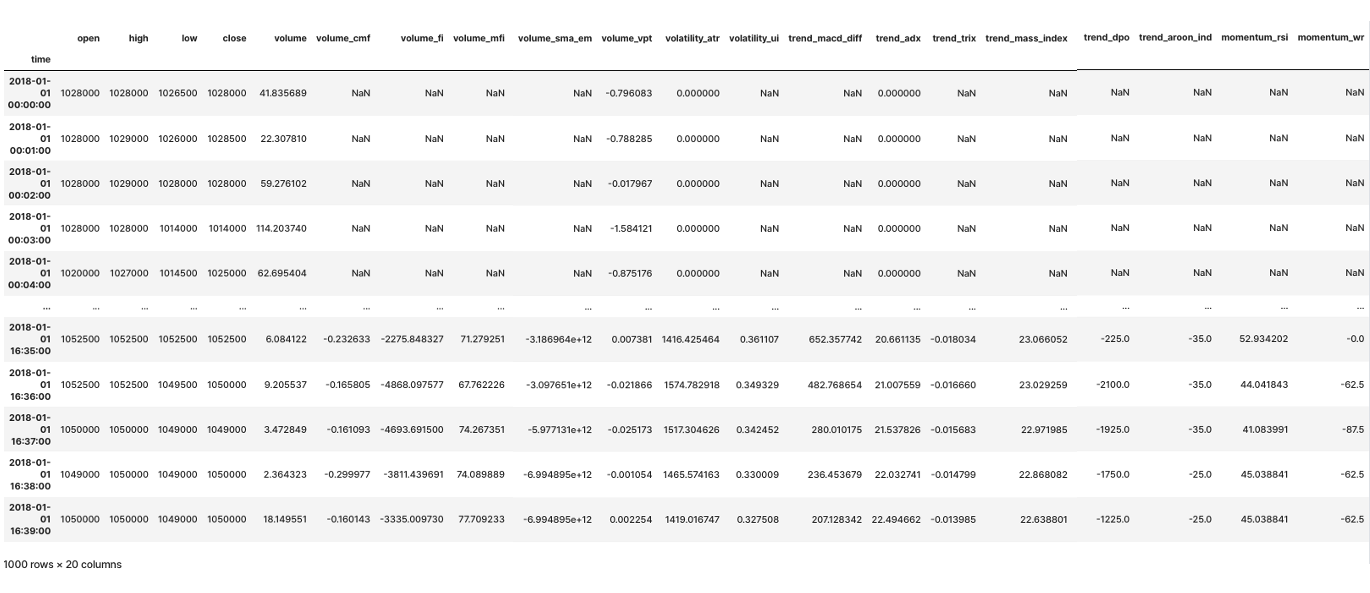

수익률 / 변동성 지표

• 수익률, 변화율 지표

  • 종가, 직전 n-영업일 가격 비율
    • $R_t$ = $close_t \over close_{t-n}$ $- 1$
  • 금일 거래량, 직전 n-영업일 거래량 비율
    - $VolumeChange_t$ = $volume_t \over volume_{t-n}$ $- 1$
    
    

• 변동성 지표

  • 종가의 n-영업일 이동표준편차
  • 거래량의 n-영업일 이동표준편차

• 모멘텀 및 수익률 계산, 표준편차 계산

windows_mom = [5, 10, 20]
windows_std = [30]

for i in windows_mom:
    df_[f'vol_change_{i}'] = df_.volume.pct_change(i).round(6)
    df_[f'ret_{i}'] = df_.close.pct_change(i).round(6)

for i in windows_std:
    df_[f'std_{i}'] = df_.close.rolling(i).std()
    df_[f'vol_std_{i}'] = df_.volume.rolling(i).std()

# result
df_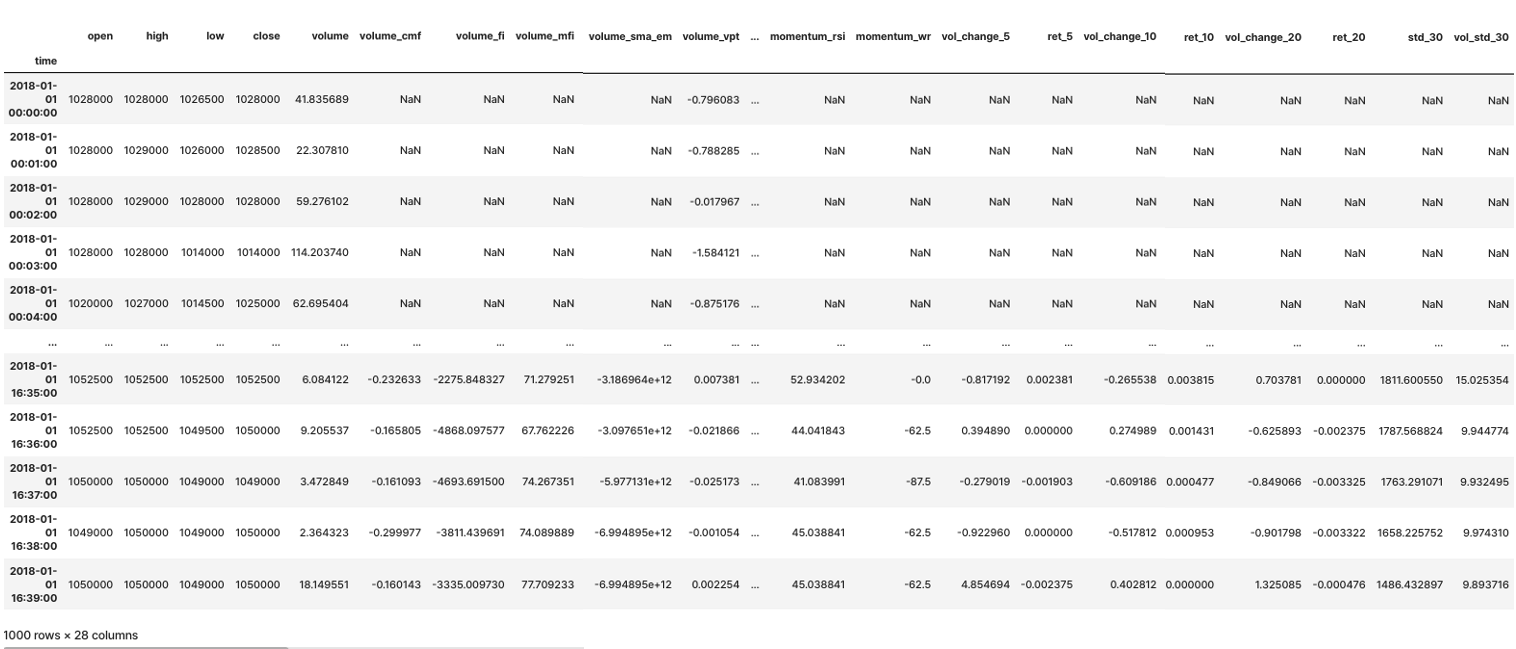

• 학습을 위한 데이터셋 가공 및 분리

df_tmp_data = df_.join(df_label_data).dropna()
X, y = df_tmp_data.iloc[:, 5:-1], df_tmp_data.iloc[:, -1]

sc = StandardScaler()
X_sc = sc.fit_transform(X)
X_sc = pd.DataFrame(X_sc, index=X.index, columns=X.columns)

X_sc.head()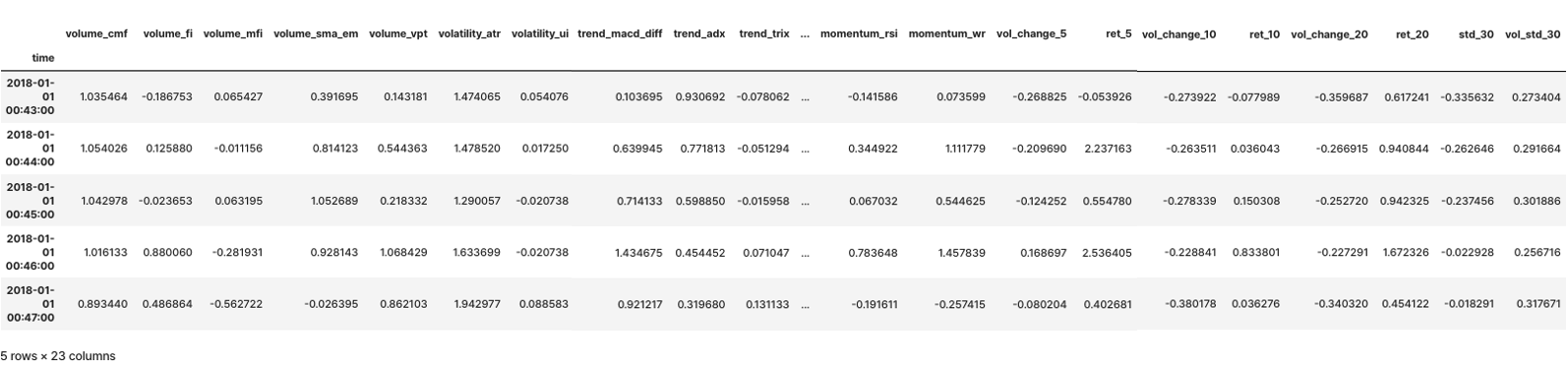

• RF

rfc = RandomForestClassifier(class_weight='balanced')
rfc.fit(X_sc, y)

Feature Selection methods

• Feature Selection
  • MDI
  • MDA
    
    
• Sequential Feature Selection
  • RFE CV
  • SFS
    
    
• Shapley Additive explanations
  • SHAP

Feature Selection

MDI

• Mean Decrease Impurity
• 트리 계열 분류기에서 산출되는 Feature Importance 값 사용
  • In-Sample(훈련 데이터셋 정확도 기반)
  • 모든 피쳐가 어느 정도의 중요도
  • 모든 Feature Importance 합은 1
  • substitution effect는 해결 못함(상품 또는 서비스의 가격 변화로 인해 소비자가 다른 상품을 구매하도록 유도하는 것)

feat_imp = imp.mean_decrease_impurity(rfc, X.columns)
feat_imp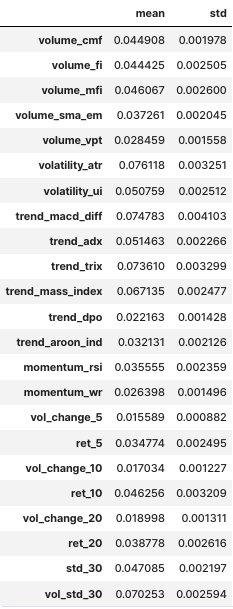

MDA

• Mean Decrease Accuracy
• 트리 계열이 아니더라도 사용 가능
  • Out-of-Sample(훈련 데이터셋 기준 정확도 추출, OOS)
  • Accuracy를 포함해 많은 성능 지표 사용 가능
  • 이 역시, substitution effect는 해결 못함
  • 모든 피쳐가 중요하지 않게 나올 수 있음!
• 연산 방법
  • 분류기 fitting
  • 성능 지표에 따른 OOS 측정
  • 각 피쳐에 대해 무작위로 섞은 다음 OOS를 측정하고 기존값과 비교(전체 피쳐에 대해서 모두 수행)

• SVC 모델

svc_rbf = SVC(kernel='rbf', probability=True)
cv = KFold(n_splits=5)
feat_imp_mda = imp.mean_decrease_accuracy(svc_rbf, X_sc, y, cv_gen=cv)

• plot_feature_importance 함수

def plot_feature_importance(importance_df, save_fig=False, output_path=None):
    # Plot mean imp bars with std
    plt.figure(figsize=(10, importance_df.shape[0] / 5))
    importance_df.sort_values('mean', ascending=True, inplace=True)
    importance_df['mean'].plot(kind='barh', color='b', alpha=0.25, xerr=importance_df['std'], error_kw={'ecolor': 'r'})
    if save_fig:
        plt.savefig(output_path)
    else:
        plt.show()

• MDI : plot_feature_importance(feat_imp)
  

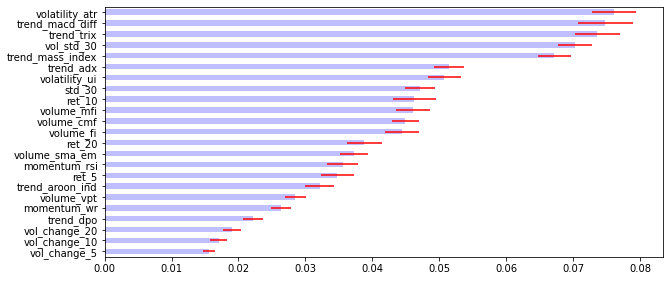
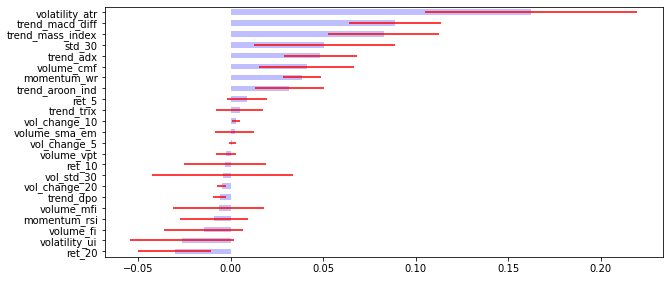
• MDA : plot_feature_importance(feat_imp_mda)
  

Sequential Feature Selection

RFE CV

• Recursive Feature Elimination
• RFE에 CV 도입
• 데이터셋을 K개로 분할 및 학습, 검증 진행
  • Feature 기여도에 따라서 삭제 여부 결정
• Validation 성능이 최고치인 경우를 최종 Feature로 선정

svc_rbf = SVC(kernel='linear', probability=True)
rfe_cv = RFECV(svc_rbf, cv=cv)
rfe_fitted = rfe_cv.fit(X_sc, y)

rfe_df = pd.DataFrame([rfe_fitted.support_, rfe_fitted.ranking_], columns=X_sc.columns).T.rename(columns={0:"Optimal_Features", 1:"Ranking"})
rfe_df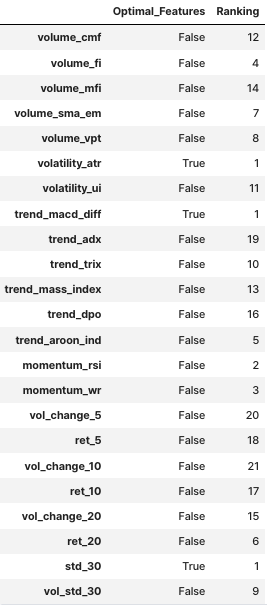

rfe_df[rfe_df["Optimal_Features"]==True]

SFS

• Sequential Feature Selection
• 순차 진행 방식
• 순서대로 Feature를 빼거나 더하는 방식으로 최적 조합을 찾음
  • Backward, Forward 다 사용 가능
    • Backward : 모든 피쳐에서 시작 -> 피쳐를 하나씩 빼면서 진행
    • Forward : Null에서 시작 -> 피쳐를 하나씩 더하면서 진행

n = 2

sfs_forward = SequentialFeatureSelector(svc_rbf, n_features_to_select=n, direction='forward')
sfs_fitted = sfs_forward.fit(X_sc, y)

sfs_rank = sfs_fitted.get_support()
sfs_df = pd.DataFrame(sfs_rank, index=X_sc.columns, columns={"Optimal_Features"})

sfs_df [sfs_df ["Optimal_Features"]==True].index

SHAP

• Shapley Additive explanations

Shapley Value?

• 다수의 플레이어에게 공정한 상, 벌을 배분하기 위한 솔루션
• 플레이어별 공헌도는 상이하나 상호간 이득 및 손실을 주고받는 상황에 적용
• 최대 성과를 위한 의사결정 -> 연쇄적 수행 -> 이를 통해 얻은 게임 결과에서 그 플레이어에게 기대할 수 있는 평균 한계 공헌도를 측정 -> 이것을 Shapley Value라고 함

import shap
explainer = shap.TreeExplainer(rfc)
shap_value = explainer.shap_values(X_sc)

shap.summary_plot(shap_value, X_sc)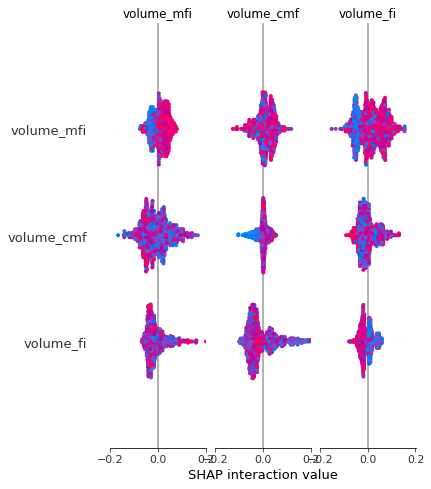

• 결과 별도 저장

output_file_name = os.path.join(DATA_PATH, 'sub_upbit_eth_min_feature_labels.pkl')
df_tmp_data.to_pickle(output_file_name)

10-4. Model Training

---

기본 설정

• 라이브러리 import

import datetime
import sys
import os
import re
import io
import json
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import ta

from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import KFold
from sklearn.ensemble import RandomForestClassifier, BaggingClassifier
from sklearn.metrics import accuracy_score, precision_score, recall_score, confusion_matrix, f1_score, roc_auc_score, roc_curve

sys.path.append('/aiffel/aiffel/fnguide/data/')
from libs.mlutil.pkfold import PKFold

• 데이터셋 로드

DATA_PATH = '/aiffel/aiffel/fnguide/data/'
data_file_name = os.path.join(DATA_PATH, 'sub_upbit_eth_min_feature_labels.pkl')

• t-value

df_data = pd.read_pickle(data_file_name)
df_data['t_value'] = df_data['t_value'].apply(lambda x: x if x == 1 else 0)

df_data['t_value'].value_counts()

• train 데이터 및 test 데이터 비율 조정

train_ratio, test_ratio = 0.7, 0.2
n_train = int(np.round(len(df_data) * train_ratio))
n_test = int(np.round(len(df_data) * test_ratio))

• StandardScaler

X, y = df_data.iloc[:, 5:-1], df_data.iloc[:, -1]

sc = StandardScaler<()
X_sc = sc.fit_transform(X)

• train 데이터 및 test 데이터셋 분할 및 일부 사용 설정

train_x, test_x, train_y, test_y = X_sc[:n_train, :], X_sc[-n_test:, :], y.iloc[:n_train], y.iloc[-n_test:]

train_x = pd.DataFrame(train_x, index=train_y.index, columns=X.columns)
train_y = pd.Series(train_y, index=train_y.index)
test_x = pd.DataFrame(test_x, index=test_y.index, columns=X.columns)
test_y = pd.Series(test_y, index=test_y.index)

train_x = train_x[:1000]
train_y = train_y[:1000]

Purged K-fold for Cross-Validation

• Purged?
  • 학습 데이터 및 검증 데이터 분할 시, 두 시계열 사이 연관성을 최대한 배제하는 방법론
  • 시계열 집합 간 일종의 시간차를 두는 방식
    • 모든 관측값에 대한 학습 데이터 및 검증 데이터의 상관도를 줄이기 위함

기존 K-fold CV 단점

• 관측치가 IID 상태에서 추출되었다고 보기 어려움
• 테스트 집합도 모델 개발 과정에서 반복 사용되었을 가능성이 매우 높음 ➡️ 여러 편향이 반영되었을 수 있음
• 이로 인해, 학습 데이터와 검증 데이터의 유사 패턴이 점점 많이 담기게 되어 Leakage(정보의 누수) 정도가 심해지는 경향을 보임(분류기 성능의 객관성이 크게 떨어지는 것)

• PKFold 클래스로 구현

n_cv = 4
t1 = pd.Series(train_y.index.values, index=train_y.index)

cv = PKFold(n_cv, t1, 0)

Find the best param for bagging(RandomForest) with grid-search

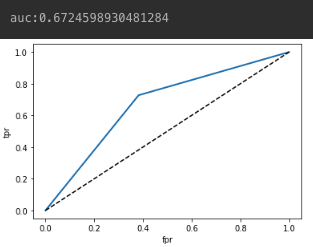
• ROC 커브 : 다양한 임계값에서의 모델 분류 성능 측정 그래프
  • AUC 값이 1에 가까워질수록 ➡️ 좋은 성능으로 봄
  • FDR : 모델이 음성 sample을 양성으로 잘못 예측하는 비율
  • TPR : 모델이 양성 sample을 양성으로 잘 예측하는 비율

• RF를 이용한 분류기 학습
  • GridSearchCV에 넣을 파라미터 임의 지정 + RF 학습
  • 결과값을 배깅 방식으로 학습(오차 분산을 줄이기 위함)
  • bc_params 사용, GridSearch 클래스 사용 -> fitting
    • GridSearchCV 수행을 위해 지정했던 파라미터
  • bestestimator 기반 분류기 결과값을 통해 성능 판단

• 검증 오차

  • 예측 시 오차가 발생
    • 그 오차를 줄이기 위해, 오차 평균이 0에 가깝도록 조정해야 함
    • 오차 평균이 0이 아니면 편향되었다고 표현
    • 불편 추정량 : 예측하고자 하는 실제값과 오차가 0인 값
  
  

• 과대적합 및 과소적합

  • overfitting : 오차 평균 편향, 분산 큼
  • underfitting : 오차 평균 편향, 분산 작음

  이러한 오차 분산을 줄이기 위해 Bagging을 쓰는 것

  
  

• 하이퍼파라미터 튜닝 수행(18분 소요됨)

bc_params = {'n_estimators': [5, 10, 20],
             'max_features': [0.5, 0.7],
             'base_estimator__max_depth': [3,5,10,20],
             'base_estimator__max_features': [None, 'auto'],
             'base_estimator__min_samples_leaf': [3, 5, 10],
             'bootstrap_features': [False, True]
            }
            
rfc = RandomForestClassifier(class_weight='balanced')
bag_rfc = BaggingClassifier(rfc)
gs_rfc = GridSearchCV(bag_rfc, bc_params, cv=cv, n_jobs=-1, verbose=1)
gs_rfc.fit(train_x, train_y)
gs_rfc_best = gs_rfc.best_estimator_

• 위에서 얻은 최적 모델을 써서 다시 모델 학습

gs_rfc_best.fit(train_x, train_y)

• 테스트 데이터에 대한 예측 수행

pred_y = gs_rfc_best.predict(test_x)
prob_y = gs_rfc_best.predict_proba(test_x)

• 성능 지표

confusion = confusion_matrix(test_y, pred_y)
accuracy  = accuracy_score(test_y, pred_y)
precision = precision_score(test_y, pred_y)
recall    = recall_score(test_y, pred_y)

print('================= confusion matrix ====================')
print(confusion)
print('=======================================================')
print(f'정확도:{accuracy}, 정밀도:{precision}, 재현율:{recall}')

• ROC Curve 및 AUC 계산 시각화
  • AUC를 봤을 때, 그렇게 좋은 성능을 낸다고 보기는 어려울 것 같은 수치가 나옴

fpr, tpr, thresholds = roc_curve(test_y, pred_y)
auc = roc_auc_score(test_y, pred_y)
plt.plot(fpr, tpr, linewidth=2)
plt.plot([0, 1], [0, 1], 'k--')
plt.xlabel('fpr')
plt.ylabel('tpr')
print(f'auc:{auc}')