차원축소 란?
-
매우 많은 feature로 구성된 다차원 데이터 셋의 차원을
축소해 새로운 차원의 데이터로 변경하는 것 -
데이터 끼리의 관계를 학습해서 관계성 기반으로
새로운 feauture를 만드는것 (늘어날 수도 있다)
- Feature Selection
- 특정 Feature에 종속성이 강한 불필요한 Feature 제거
우리 목적의 불필요한 Feature를 날림 - 차원축소의 목적이 손실(좋은 손실)일 때도 있다
ex) mp3 = 사람들은 못 듣는 주파수를 지움
- 특정 Feature에 종속성이 강한 불필요한 Feature 제거
- Feature Extraction
- 기존 Feautre를 저차원의 중요 Feature로 압축해서 추출
- 데이터 끼리의 관계를 학습해서 관계성 기반으로
새로운 feauture를 만드는것
차원축소하는 이유
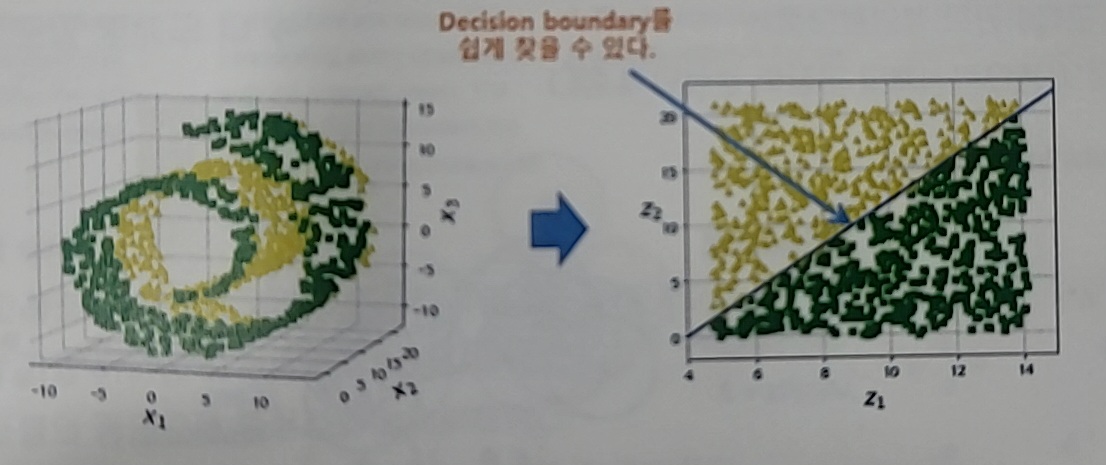
차원의 저주(Curse of dimension)
-
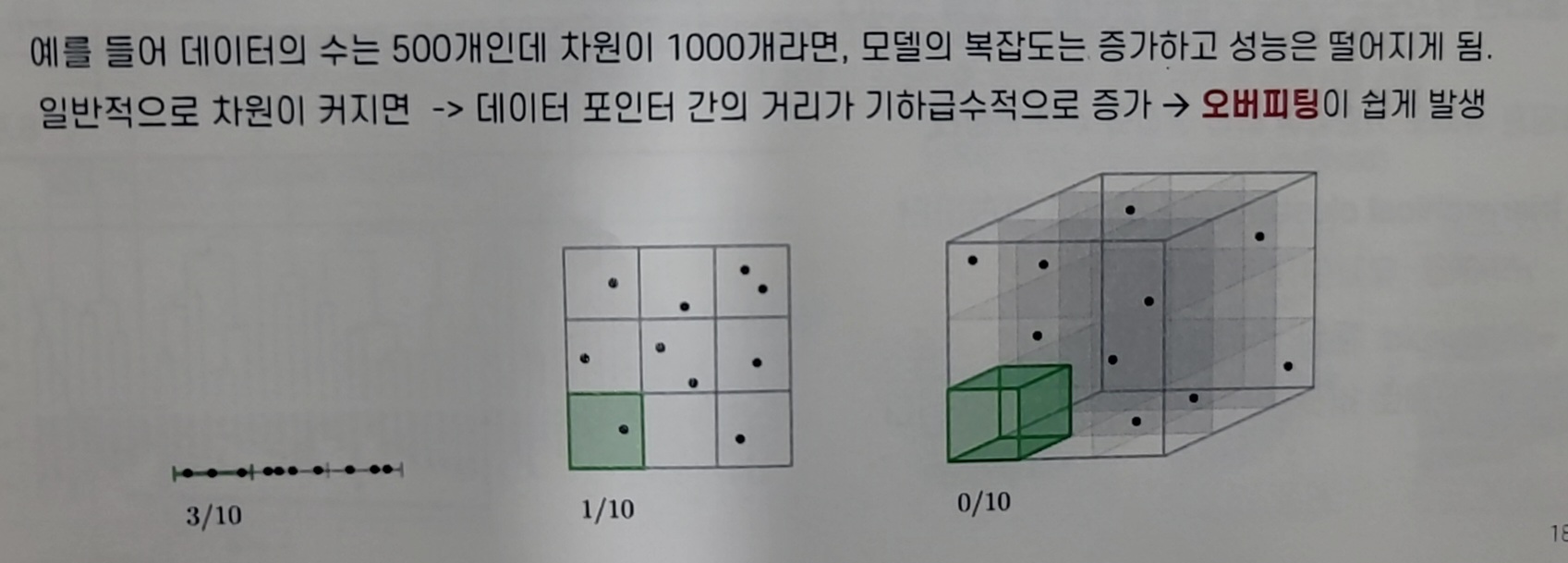
데이터 학습을 위한 차원(=특성,변수,피쳐)이 증가하면서 학습데이터의 수 보다 차원의 수가 많아지게 되어 모델의 성능이 떨어지는 현상(오버피팅이 쉽게 발생)
-
데이터가 증가하면서 차원의 수가 많아 져서 데이터가 희소해져서 어려워 져서 모델의 복잡도가 증가 -> 오버피팅
차원의 수가 많아진다는 것 = Feature 수가 늘어나는 것
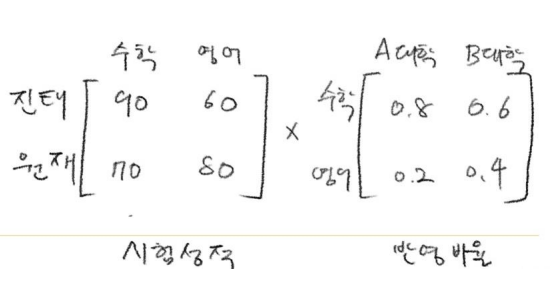
행렬의 절대적 법칙 2가지
-
행렬의 곱에서는 앞의 가로와 뒤의 세로와 갯수가 같아야한다.
-
행렬의 곱은 가운데 있는 행과 열은 없어진다.
(수학, 영어는 사라진다)
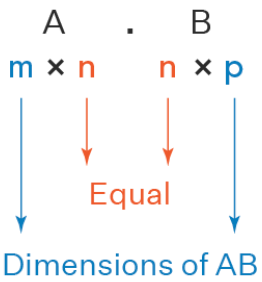
! ! 꼭 알아 두기 ! !
인코딩(Encoding)
-
압축하는 역할
-
Original Space에서 A를 압축한 공간을 Latent Space
복원된 공간은 Original Space
하지만 복원된 데이터는 A와 유사한 A프라임 데이터
디코딩(Decoding)
-
압축된 정보로 부터 복원하는 역할
-
노이즈 제거
- ex) 코끼리의 가죽의 상처를 복구하지 않는것..
- 불필요한 요소를 없앰
-
숨겨졌던 잠재적 관계가 나옴
- 손실 자체가 나쁘긴 하지만 아주 잘 손실하는건 중요
손실을 잘 일으키려면 데이터를 잘 알아야 하기 때문
- 손실을 잘 한다는건 중요한건 남겨두고
불필요한걸 제거 하는것을 의미한다
- 손실 자체가 나쁘긴 하지만 아주 잘 손실하는건 중요
Latent Factor(잠재요인 "Z"로 표현)
- 겉으로 들어나 있지 않지만 내재적으로 숨겨져있는 요인
행렬 분해(matrix Factorization)
- 사용자-아이템 상호 작용 데이터를 모델링 하기 위해
사용자와 아이템을 잠재적인 요인(특성)으로 분해하여
추천 시스템에 활용
활용 방안
-
Original feature를 새로운 feature 1,2,3로 재해석 (3차원)
-
추천 알고리즘에 사용(코싸인 유사도 사용)
-
Contents-Based Recommendation System
(컨텐츠 기반 추천 시스템) -
Collaborative Filtering (협업 필터링)
차원 축소 방법
- 행렬 분해
- Manifold Learning
행렬 분해(MF)의 종류
SVD, PCA 가 제일 잘 사용되며 중요하다!
SVD (Singluar value Decomposition)
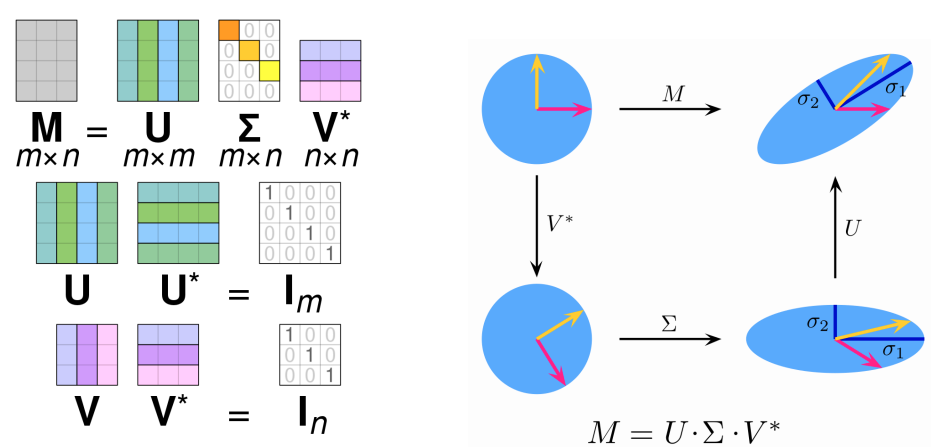
선형 대수 기반의 차원 축소 방법
임의의 행렬을 세 개의 행렬 곱으로 분해하는 방법
데이터 간 잠재 요인을 추출한느 곳에 많이 사용 된다
SVD = 특이값 분해
- 특징 : 행렬 3개로 분해
- 활용 : 다양함
PCA (Principal component analysis)
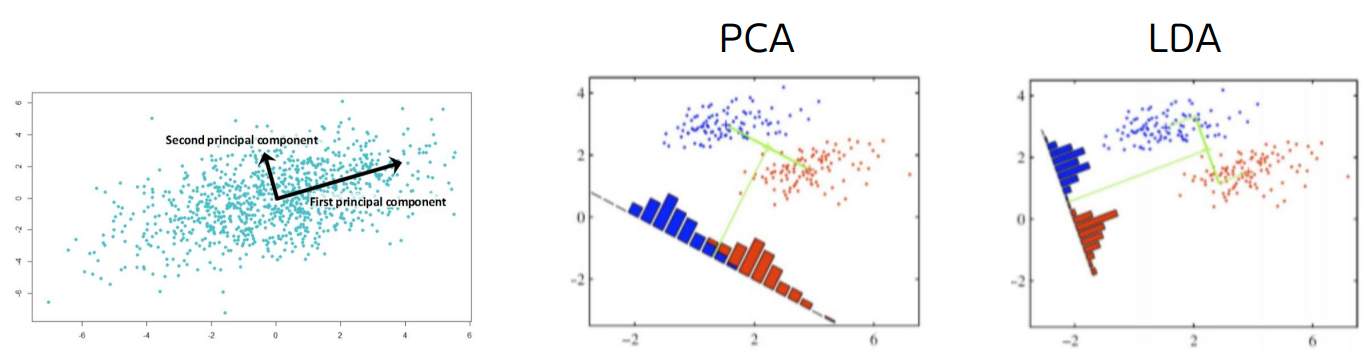
시각화에서 뭐를 사용해야할지 모르겠다면
PCA를 사용..
PCA = 주성분 분석
-
목적 : 원본 데이터의 분산(퍼진모양)이
축소 되었을 때에도 최대한 잘 유지되어야 한다. -
제 1주성분 = 분산이 가장 방향(주성분)을 찾고 분산이 가장 작은 방향을 누름
-
제2 주성분 = 제 1주성분과 직교(수직)하며,
데이터의 분산이 두 번째로 큰 방향ex) 텀블러 -> 텀블러의 면적을 최대한 유지하기 위해
살짝 기울인 상태에서 누름 -
특징 : 펼쳐져 보이게 누름
-
활용 : 시각화
LDA (Linear Discriminant Analysis)
분류에 사용할 때는 PCA가 아닌 LDA를 사용
LDA = 선형판별분석법
-
목적 : 클래스간의 구분
누른 후에 파랑색과 빨강색이 잘 구분되어야 한다 -
특징 : 구분가능하게 누름
-
활용 : 시각화

NMF (Non-negative Matrix Factorization)
저차원 행렬과 양수인 가중치 벡터로 분해하는 방법
요인들의 양 적인 합으로 결과로 해석하고 싶어서 사용
NMF = 비음수 행렬 분해
- 특징 : 음수가 하나도 없음
- 활용 : 군집화
차원축소 시각화 사용법
데이터 불러오기
# 손글씨 이미지를 불러와 확인해보자
from sklearn.datasets import load_digits
digits = load_digits()
fig, axes = plt.subplots(2, 5, figsize=(10, 5))
for ax, img, label in zip(axes.ravel(), digits.images,
digits.target):
ax.imshow(img)
ax.set_title(f'target : {label}')PCA
고차원의 데이터를 분산이 가장 큰 방향을 고려하여
내가 원하는 크기의 저차원으로 압축시키는 행렬 분해를
기반으로 한 모델
from sklearn.decomposition import PCA
pca_model = PCA(n_components = 2) #몇차원 줄일지 정해줘야 한다
digits_pca = pca_model.fit_transform(digits.data)
digits_pca
# 시각화를 통해 학습결과를 확인해보자
colors = ["#476A2A", "#7851B8", "#BD3430", "#4A2D4E",
"#875525","#A83683", "#4E655E", "#853541", "#3A3120",
"#535D8E"] #숫자를 구분하기 위해 color를 미리 지정한다
plt.figure(figsize=(12, 12))
plt.title('PCA', fontsize = 30)
plt.xlim(digits_pca[:, 0].min(), digits_pca[:, 0].max() + 1)
plt.ylim(digits_pca[:, 1].min(), digits_pca[:, 1].max() + 1)
for i in range(len(digits.data)):
# 숫자 텍스트를 이용해 산점도를 그리는 코드
plt.text(digits_pca[i, 0], digits_pca[i, 1],
str(digits.target[i]),
color = colors[digits.target[i]], fontsize = 12)
plt.xlabel("PCA feature 1")
plt.ylabel("PCA feature 2")t-SNE(어려워서 pass가능..)
t-SNE는 주로 높은 차원의 데이터를 시각화하기 위해 사용
3개 보다 높은 개수의 특성을 뽑는 경우가 거의 없으며
지도 학습용보다는 데이터 탐색을 위주로 사용한다.
목적
-
데이터 포인트 사이의 거리를 가장 잘 보존하는
(데이터를 잘 구분하는) 저차원 표현을 찾는 것 (Manifold) -
t-SNE를 사용하면 원본 데이터 공간(높은 차원)에서 비슷한 데이터는 낮은 차원의 공간에서 가깝게 위치하며, 비슷하지 않은 데이터 구조는 멀리 떨어져 위치하게 된다.
-
다량의 데이터도 잘 시각화 할 수 있는 U-MAP도 많이 쓰인다.
# t-SNE
from sklearn.manifold import TSNE
model = TSNE()
model
digits_tsne = model.fit_transform(digits.data)
digits_tsne
# 시각화를 통해 학습결과를 확인해보자
colors = ["#476A2A", "#7851B8", "#BD3430", "#4A2D4E",
"#875525", "#A83683", "#4E655E", "#853541", "#3A3120",
"#535D8E"] #숫자를 구분하기 위해 color를 미리 지정한다
plt.figure(figsize=(12, 12))
plt.title('t-SNE', fontsize = 30)
plt.xlim(digits_tsne[:, 0].min(),
digits_tsne[:, 0].max() + 1)
plt.ylim(digits_tsne[:, 1].min(),
digits_tsne[:, 1].max() + 1)
for i in range(len(digits.data)):
# 숫자 텍스트를 이용해 산점도를 그리는 코드
plt.text(digits_tsne[i, 0], digits_tsne[i, 1],
str(digits.target[i]),
color = colors[digits.target[i]], fontsize = 12)
plt.xlabel("t-SNE feature 1")
plt.ylabel("t-SNE feature 2")