군집화란?
-
데이터 사이의 유사성을 통해서 같은 카테고리일 것으로 예상되는 것들을 묶어 내는 것
-
지도학습은 색이 지정되어있음(정답이 있다)
-
비지도학습은 정답이 없다
-
유사성(데이터간의 거리)을 보고 조배정
-
군집화는 라벨이 없는 데이터를 학습을 통해서 라벨을 묶어주는것
(색이 없는걸 색을 칠해줌)
Clustering 방법
- K-means
- DBSCAN
- Hierarchhical
K-means 란?
-
가장 일반적으로 사용되는 클러스터링 알고리즘
-
데이터를 K개의 클러스터로 나누는데 사용
-
알고리즘이 쉽고 간결하지만 효율적이어서 여전히 자주 사용
-
중심점(centroid)라는 특정한 임의의 지점을 선택하여 해당 중심에 가장 가까운 포인트들을 선택하는 기법
K-means = 최적의 클러스터 수, 시작점이 중요!
동작 방법
- 첫번째 작업은 중심점의 초기값을 설정하는 것
초기 값은 임의로 K개를 선택한다.- 각 중심점에서 가장 가까운 포인트들을 선택한다.
- 각 군집 포인드들의 평균으로 중심점을 업데이트한다.
- 2~3번을 반복하다가 더이상 중심점 이동이
없을 경우에 중단한다.
K-means의 2가지 방법
-
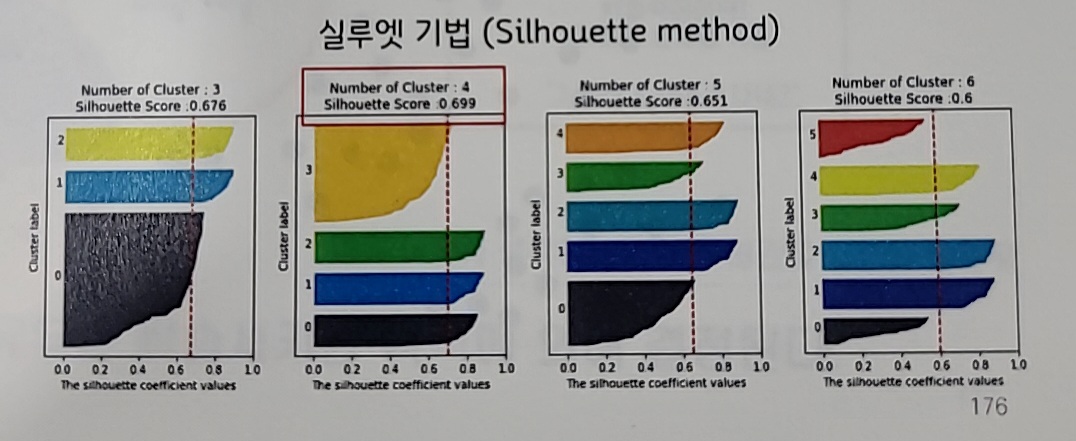
실루엣 기법(Silhouette method)
응집도와 분리도로부터 실루엣 스코어를 계산하여
가장 값이 클 때의 K를 선정-
같은 클러스터 가깝게 뭉침
-
다른 클러스터 끼리 멀리 떨어져야 한다.
-
-
엘보우 기법(Elbow method)
클러스터 내 오차 제곱합(SSE)이 크게 줄어들다가
완만하게 꺾이는 부분의 K를 선정-
다른 클러스터를 생각하지말고
클러스터 내부의 응집도만 고려 -
클러스터 내부의 평균 거리가 가장 큰걸 잘라버리면서
확 줄어드는 평균 거리가 짧아지는 지점을 본다. -
효과가 근단적으로 떨어지다가
완만해 지는 부분을 찾는것 -
어디가 엘보우인지 찾기 힘들 때가 있다.
(완만한곡선)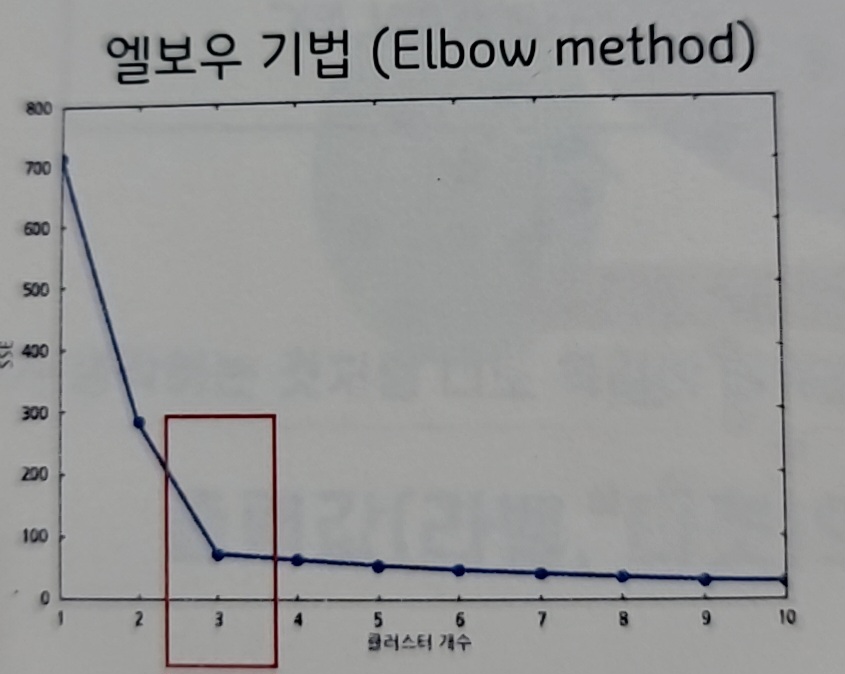
-
K-means의 단점
-
클러스터의 수(K)를 사전에 지정해야 한다
-
K개수를 선택하는 것이 애매할 경우가 많다
-
초기 K의 설정 위치에 따라 결과값이 많이 달라진다
-
복잡한 형태의 군집은 불가능(이상치에 민감하게 반응)
-
클러스터의 형태가 구형이 아닌경우
or 크기가 많이 다를경우 성능이 저하된다.
K-Means의 주요 Parameter
-
init
초기 군집 중심점의 좌표를 설정할 방식,
기본값은 'k-means++' -
n_clusters
군집화할 개수, 즉 군집 중심점의 개수, 기본값은 8 -
max_iter
중심점 이동 최대 반복 횟수, 기본값은 300
max_iter 횟수만큼만 학습을 반복 한다
만약, max_iter 이전에 더이상 중심점 이동이 없다면
학습을 중단한다
주요 Attributes
-
cluster__centers_
군집 중심점의 좌표
(Coordinates of cluster centers) -
labels_
각 데이터 포인트들의 label값
(Labels of each point) -
inertia_
각 데이터에서 해당 군집의 중심점까지의 거리 제곱합
(Sum of squared distances of samples
to their closest cluster center.) -
n_iter_
반복 실행 횟수
(Number of iterations run.)
K-means 사용방법
from sklearn.cluster import KMeans
#모델 빌드
model = KMeans(n_clusters = 3)
#모델 학습
model.fit(input_feature)#비지도학습이라 target이 없다
# 클러스터링 결과 확인
input_feature[:5]
model.labels_
model_pp = KMeans(n_clusters=3,
random_state = 0).fit(input_feature)
import matplotlib.pyplot as plt
center = model.cluster_centers_
# 그림그려보기
plt.figure(figsize=(8, 6))
for i in range(K):
plt.scatter(input_feature[model.labels_ == i, 0],
input_feature[model.labels_ == i, 1], marker='o',
c=f'C{i}', edgecolor='k', lw=0.5)
c = center[i]
plt.scatter(center[i][0], center[i][1], s=200, c="y",
edgecolor='k', lw=1)
plt.legend([str(i) for i in range(K)])
plt.show()
DBSCAN 란?
DBSCAN은 군집의 개수를 지정하는 것이 아니라
일정 밀도 이상이 군집이라고 정의함으로서
밀도를 지정함으로 자동으로 N개의 군집이 생성되게 한다.
-
밀도 기반의 공간 클러스터링의 알고리즘
-
데이터 포인트 간의 밀도를 기반으로 클러스터를 형성
-
잡음(noise)을 포함하는 데이터에 잘 작동
-
2개로 밀도가 정의된다.
- esp(반지름)
- min pts(단위 면적 내 최소 data수)
-
원 안에 일정 갯수가 없으면 제외 해버린다(outlier)
집어 넣고 싶다면 반지름의 크기를 넓히면 된다.
사용처
ex) 위성 이미지분석, 생물 정보학, 도시 계획 등과 같이
복잡하거나 잡음이 많은 데이터셋에 효과적이다.
DBSCAN의 단점
- esp와 min_samples 파라미터의 설정에 민감하다
- 밀도가 일정하지 않은 데이터셋에서는 성능이 저하
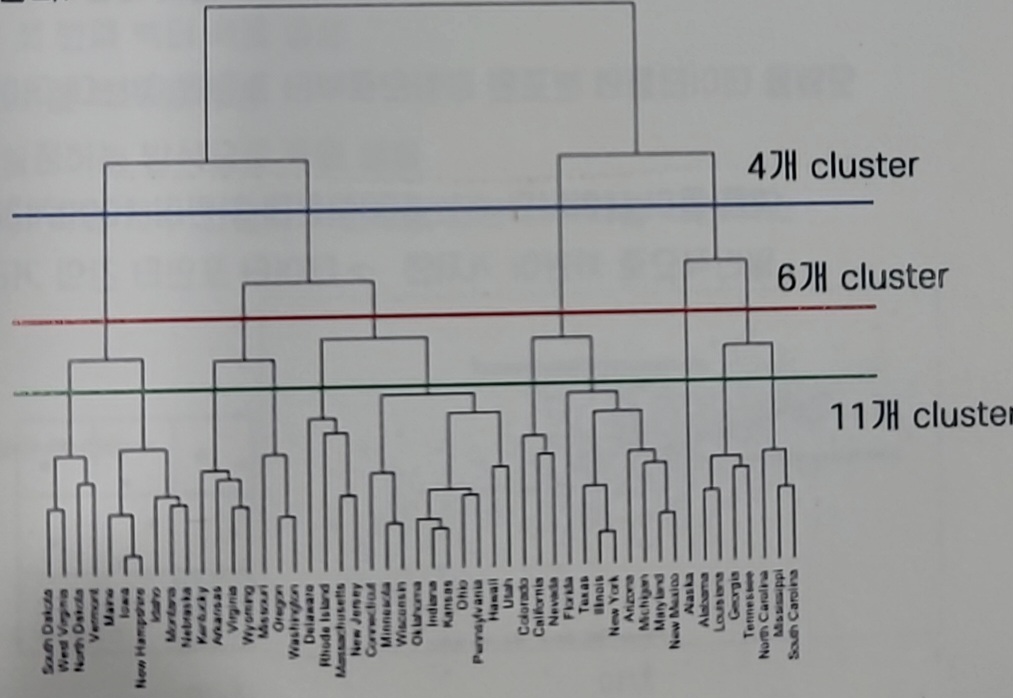
Hierarchical 이란?
전제
동일한 클러스터 내의 데이터는 유사하고 다른 클러스터끼리의 데이터는 유사하지 않다.
그렇다면 유사도만으로도 군집을 판단할 수 있을 것이다.
-
계층적 구조를 나타내는데 사용한다
-
유사도를 기준으로 친하고 안친함을 기준으로 선을 그어버림
-
2개로 비슷한 것과 다른 것이 정의 된다
- metric = 유사도 계산방식
- threshold = 동일 cluster가 되기 위한 기준
- 시각적으로 이해하기가 쉽다
- 모든 데이터간의 유사도 거리를 계산해야만한다
많은 데이터가 있다면 계산 비용이 많이 든다