Linear Regression_LG Aimers(7)

본 포스트는 LG Aimers 활동에 참여하며 온라인 AI 교육을 정리한 내용입니다!
프로그램에 관심이 있으시다면 https://www.lgaimers.ai/ 를 참고해주세요!!

Linear models

• $h_w(x) = \theta_0 + \theta_1k_1(x_1) + ... + \theta_dk_d(x_d) = \theta^Tk(x)$
• Hypothesis 함수 H가 입력 feature와 model parameter의 linear combination으로 구성된 것
• x는 d-dimention이므로 $x_0 = 1$을 의미한다.
• 선형 모델이라고 해서 반드시 입력 변수의 선형일 필요는 없다.

Feature organization(일반화)

• $h_w(x) = \theta_0 + \theta_1k_1\phi(x_1) + ... + \theta_d\phi(x_d) = \theta^Tk_d\phi(x)$
• 입력 x가 $\phi$와 결합을 하여 hypothesis 함수를 거쳐 feature를 구성하게 된다.

Linear regression

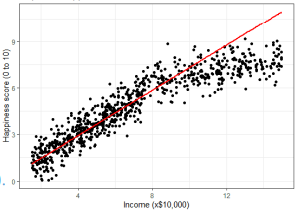
• Linear regression : 주어진 입력에 대해 출력과의 선형적인 관계를 추론하는 문제
• 모델의 파라미터를 조정하면서 주어진 data에 fitting하는 과정 중 오차가 발생하게 된다.
• 이러한 오차를 최소화해야한다.

Mean Squared Error(MSE)

$\frac{1}{2m} \sum (h_\theta(x^i)-y^i)^2$

• y는 dataset의 정답이고, h(x)는 모델이 측정한 값을 의미한다.

파라미터 최적화

• $\theta_0, \theta_1$를 구하는 과정
• $||y-X\theta||_2$

Least Square problem

• $\theta$에 관한 derivative term을 구한 뒤, 0이 되도록 하는 $\theta$의 값을 구하면 최적화된 파라미터값을 구할 수 있다.
• $\theta^* = (X^TX)^-X^Ty = X^+y$

Iterative optimization - gradient descent

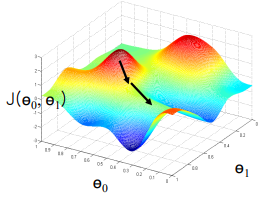
Gradient

• 함수를 미분하여 얻는 term으로 해당 함수의 변화하는 정도를 표현하는 값

gradient descent

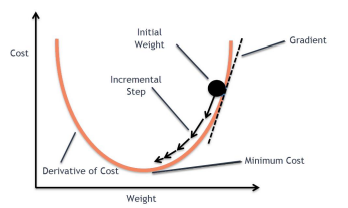
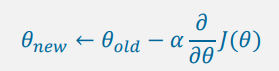
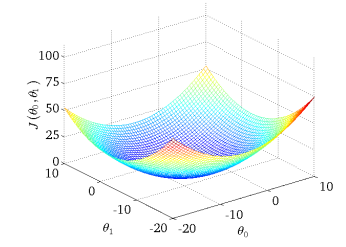
• 임의의 point에서 error surface의 최소인 point를 찾아가는 과정
• gradient가 0인 지점을 $\theta$값을 바꿔가며 찾아가는 과정
• 함수의 변화도가 가장 큰 방향으로 이동하는 것을 반복한다. → greedy method

greedy method : 현재 지점에서 가장 변화도가 가파른 방향으로 update를 하는 방식

Global Optimum

• error surface에서 가장 최소인 점
• 기울기가 0이며 가장 최소인 지점을 의미한다.

Local Optimum

• 지역적으로는 최소이지만 전체 영역을 놓고 보았을 때는 최소가 아닌 점

Gradient Descent VS Normal equation

Gradient Descent	Normal Equation
여러 번의 반복적인 과정을 통해 해를 구한다.	1 step으로 해를 구한다.
n이 크더라도 반복적으로 해를 구해나갈 수 있다.	Sample Size가 늘어나는 경우에 inverse matrix 등을 구하기 어려워진다.