[논문리뷰] Generative Adversarial Networks (GAN)

Intro

• 딥러닝 기반 생성 모델의 시작을 연, 적대적 생성 신경망 (Generative Adversarial Networks, NeuRIPS 2015, Ian et al.) 논문을 리뷰한다.

0. Premilinary

• Data는 Probability Distribution이라는 말을 들어본 적이 있을 것이다. 이 말이 대체 뭘까?

• 예를 들어, 우리에게 512x512 정도의 흑백 이미지를 만들어낸다고 가정하자. 이 이미지를 만들어낸다는 것은 512x512개의 픽셀들이 모인 1채널(Grayscale), 즉 1x65536개의 픽셀들에 0~255까지의 값을 할당하는 것이다.

• 그러면 65536개의 픽셀들에 U(0,255)에서 샘플링한 값을 할당한다고 가정하고, 이를 수천, 수만, 수십만, 수백만 번 반복해보자. 그러면 과연 유의미한 데이터가 나올까?

  • 실험적으로 측정해본 결과, 그럴듯한 이미지는 절대로 만들어지 않고 항상 인간의 눈으로 이해할 수 없는 noise들만 생성된다.
    

  • 이를 통해 데이터는 65536개의 차원 내에 균등하게 존재하는 것이 아니라 특정 분포 또는 특정 패턴의 형태로 존재한다는 것을 알 수 있다.

  • 즉 image는 65536차원의 Normal distribution은 아니고, Gaussian distribution, exponential distribution 등도 당연히 절대 아닐 것이다. 뭔가 특별하고 복잡한 distribution 상에 있을 것이고, Generative model은 이 복잡한 distribution을 추정해나가며 ‘그럴듯한’ 이미지를 생성하기 위해 학습된다.

• 이는 manifold hypothesis와도 연관성이 있는데, 실제로 데이터를 설명하는 유의미한 저차원 (manifold)가 존재한다는 가설이다.
  

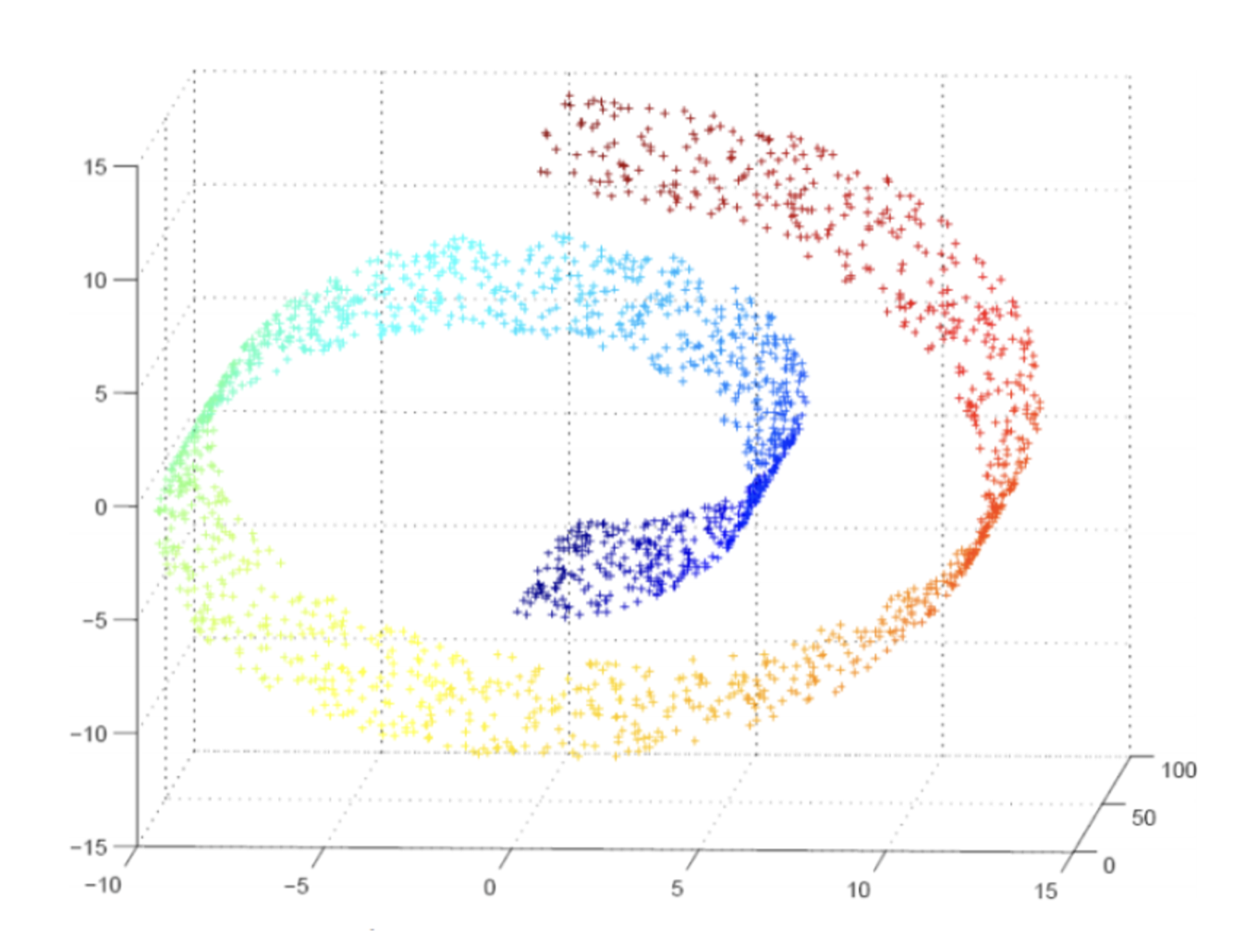
• 즉, 고차원 상에서는 거리가 가까운 데이터들이 실제로 의미상으로 가깝지 않을 수 있다. 반면, 저차원에서는 가까운 데이터를 보면 의미상으로 보다 가까움을 알 수 있다.
• 아래서도 계속 data distribution이라는 이야기를 할 것인데, 데이터들은 어떤 특별한 확률 분포 아래서 sampling된다는 것 정도로 이해해보자. 어차피 우리는 그 distribution이 무엇인지 explicit하게 밝히지 않고 모델을 통해 추정해나갈 뿐이다.

1. Introduction

• Generator-Discriminator Adversarial process를 통해 data distribution을 estimating하는 새로운 framework를 제시한다.
• 2개의 model을 ‘동시에’ 학습한다. - Generator(생성자)와 Discriminator(판별자)
  • 두 model이 minmax two-player game을 통해 각자의 역할을 잘 해내도록 학습한다.
  • Generator: data의 distribution을 잘 학습하여 ‘그럴듯한’ 이미지를 생성한다. Discriminator가 real data와 fake data(generated data)를 판별하지 못하게 하는 방향으로 이미지를 생성한다. 즉, discriminator가 판별 단계에서 실수할 확률을 maximize한다.
  • Discriminator: 어떤 sample을 input으로 받아 이 이미지가 Generator가 만들어낸 이미지일 확률을 반환한다. 즉 판별을 잘 하는 방향으로 학습된다.

💡 흔히 GAN의 Generator와 Discriminator을 ‘위조지폐범과 경찰’에 비유한다. 위조지폐범은 경찰을 속일 수 있는, 진짜 같은 위조지폐를 만들 수 있는 방향으로 학습되고 경찰은 위조지폐범이 만들어낸 위조지폐를 감별할 수 있는 방향으로 학습된다!

2. Backgrounds

• 생략

3. Adversarial Nets

• generator와 discriminator은, non-linearity mapping function을 근사할 수 있는 딥러닝 모델이다. 여기서는 모두 MLP(multi-layer perceptron)이다.
  • CNN이 아니다! 본격적으로 GAN에 CNN이 적용된 것은 DCGAN이다.
• Generator의 input으로는 noise variable $p_z(z)$가 들어오고, 이는 multilayer로 represent되는 어떤 function G를 거쳐 data distribution $G(z; \theta_d)$로 mapping된다.
• 또한, discriminator로 represent되는, data distribution을 입력으로 받아 0~1 사이 scalar을 output으로 내는 또 다른 MLP $D(x; \theta_d)$를 정의한다.
  • 즉 Generator와 Discriminator 모두 MLP (Multi Layer Perceptron)이다.
• 우리는 Discriminator가 두 가지 유형의 data (진짜 데이터, 이미지 / generator가 만들어낸 이미지)에 label을 잘 할당하도록, 즉 이를 잘 구별하도록 학습한다.
• 동시에, 우리는 Generator G를 objective function $log(1-D(G(z))$를 최소화하도록 학습한다.
  • 수식의 의미를 살펴보면, D는 discriminator의 output이고 어떤 data를 입력으로 받아 이것이 real data인 것이 유력할 수록 1에 가깝게, fake data인 것이 유력할 수록 0에 가깝게 output을 내뱉는다.
  • D값이 1에 가까울 수록 objective function 값이 exponential하게 작아진다. D(G(z))가 0에 가까울 수록 Generator가 만들어낸 fake data를 입력으로 받았을 때 1에 가까운 output을 낸다는 것이다. 즉, discriminator을 잘 속이도록 학습한다.
• 이를 수식으로 풀어내면 다음과 같이 2 player min max game의 형태로 정의할 수 있고. 이것이 GAN의 loss function이다.
  • simultanieous한 learning을 통해 D(G(z))는 1/2로 수렴한다. 즉 두 모델 사이의 평형점을 찾는다.

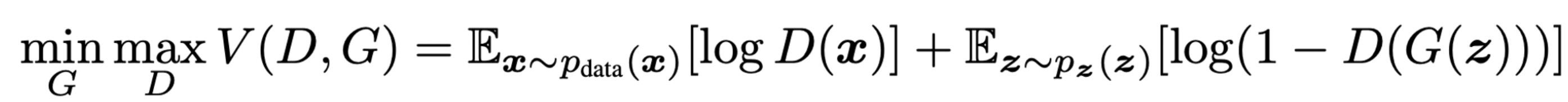
• 학습 과정을 그림으로 이해해보자.

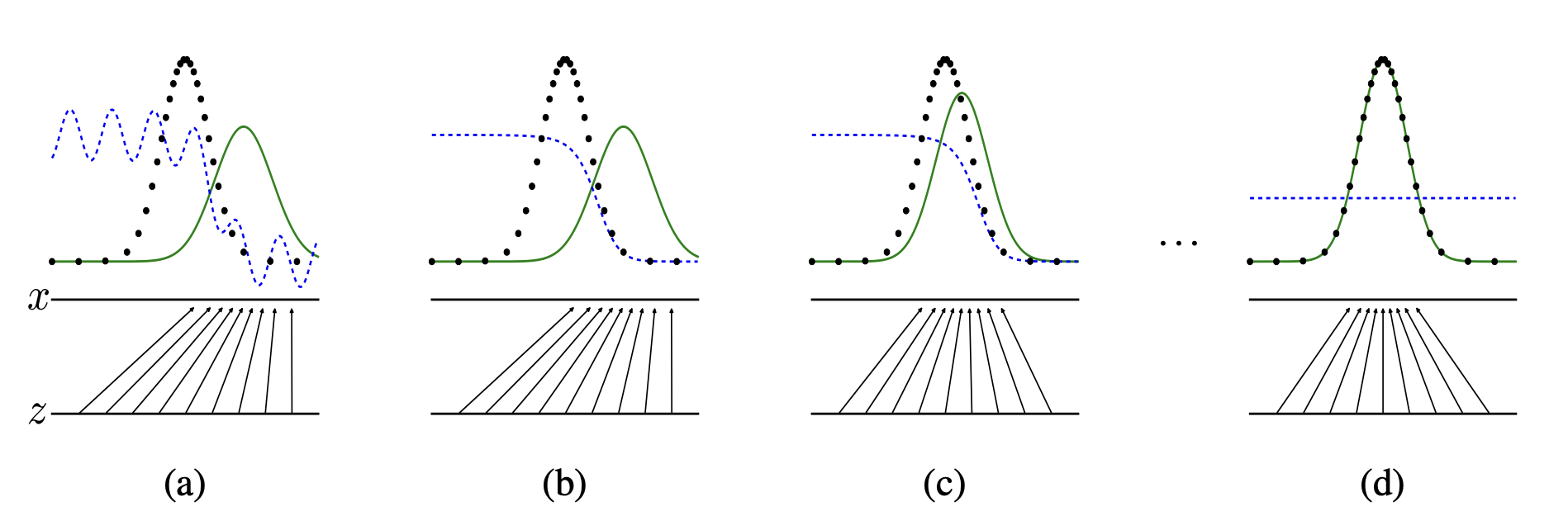
• 검은색 점선이 data distribution $p_x$, 초록색 실선이 generative distribution $p_g$이다. 그리고 파란색 점선은 학습되면서 점점 바뀌는 discriminator의 decision boundary이다.
  • (a)의 경우 data distribution과 generative distribution이 일치하지 않고, decision boundary도 일관적이지 않다.
  • (b)의 경우 generative distribution은 그대로인데, decision boundary가 조금 안정적으로 바뀌었다. 즉 discriminator가 학습된 직후를 시각화한 모습이다.
  • (c)의 경우 generative distribution이 data distribution에 가까워졌다. 즉 discriminator의 학습 이후 generator가 학습된 직후를 시각화한 모습이다.
  • (d)의 경우 (b)와 (c)를 반복하여 generative distribution이 data distribution과 유사해졌고, 이는 곧 Generator가 real data와 비슷한 이미지를 만들어낸다는 것을 의미한다. 또한, decision boundary도 pdf의 값에 대해 일관적으로 판단하고 있으므로 (이상적으로는 real data와 fake data에 대해 0.5를 내뱉을 것이다.) discriminator도 잘 학습되어 generator와 평형을 이루는 상황이다.

4. Theoretical Results

• 이런 min-max play game 기반의 학습이 잘 먹히는지를 수학적으로 뒷받침하는 섹션이다.
• GAN의 training 과정을 뒷받침하는 2가지 수학적인 증명을 유도한다.
• 수학적인 증명 이전에, 앞서 정의했던 loss function을 기반으로 학습하는 train algorithm은 다음과 같다.
• k는 hyperparameter, discriminator와 generator을 몇 대 몇 비율로 학습할 것이냐를 결정한다. (본 논문에서는 k=1, 1대1의 비율로 학습했음)
• 여기서는 전형적인 minibatch SGD로 알고리즘을 서술했는데, 다른 어떠한 optimization algorithm으로도 대체 가능하다.
• (다음 과정을 k번만큼 수행)
  • noisy한 sample들을 minibatch m개만큼 만듦.
  • 그리고 real data를 minibatch m개만큼 가져옴.
  • discriminator를 stochastic gradient ascent로 학습 (모델의 loss를 minimize하는 것과 반대로, discriminator가 더 많이 오류를 범하게 해야 하니까 gradient 방향으로 올라감), parameter update
• noisy한 sample들을 minibatch m개만큼 만듦.
• Generator을 stochastic gradient descent로 학습, parameter update

4-1. Global optimality of $p_g = p_{data}$
Proof of preposition

• Generator G가 고정되어있을 때 optimal한 Discriminator $D_G^*(x)$는 $p_{data}(x) \over {p_{data}(x)+p_g(x)}$이다.
• 증명은 기댓값 정의에 의해 V(D,G)로부터 유도되는 아래 적분식 내의 최댓값을 $alogx+blog(1-x)$ 꼴로 미분하여 극값을 구함으로써 $x = {a \over a+b}$임을 알 수 있다.

Proof of 4-1

• C(G)를 위와 같이 virtual training criterion으로 나타낼 수 있고, C(G)는 $p_g = p_{data}$일 때 global minumum $-log4$를 갖는다.
  • 직관적으로도 generative distribution이 data distribution과 완전히 같다면, discriminator은 전혀 real/fake를 구분할 수 없을 것이다. 즉 Genetor의 objective function을 optimize할 것이다.
• 위의 수식을 expectation의 정의에 의해 다음과 같은 적분식으로 바꿔주고, $log4$를 더하고 빼준 뒤 $log2$를 각 적분식의 log 안에 넣어준다.

이는 KL Divergence와 Jensen-Shannon Divergence의 정의에 의해 다음과 같은 수식들로 변환될 수 있고, JS Divergence를 최소화하는 값이 곧 C(D,G)를 최소화하는 값이다. JS Divergence는 $p_{data} = p_g$일 때 최소값 0이고 그 이외의 점에서는 양수값을 갖는다.

• 따라서 Value function을 최적화하는 값은 $p_g = p_{data}$라는 결론에 도달할 수 있다.

4-2. Convergence of Algorithm 1

• 앞서 4-1을 통해 $p_g = p_{data}$의 optimality를 증명했다. 논문에서 증명하는 것은 과연 algorithm 1을 통해 $p_g$가 $p_{data}$로 수렴하는가? 이고 이를 증명했다.
• 증명은 해석학 지식이 필요해서 생략하겠다.

5. etc

• GAN은 빠르고, high quality의 이미지를 샘플링할 수 있다는 장점이 있다.
• 하지만 GAN에는 ‘mode collapse’라는 고질적인 문제점이 존재한다.
• mode collapse는 generator가 다양한 이미지를 생성해내는 데 실패하고 비슷한 이미지만 계속 생성해내는 현상을 의미한다. 아래 사진의 MNIST 데이터셋으로 예를 들면 0~9 사이의 다양한 이미지를 생성해내는 것이 목표일 텐데, 일정 step을 밟고 나니 똑같은 데이터만 계속해서 생성해낸다.
  
• 다르게 말하면, Generator와 discriminator 사이의 균형이 무너져서 한 쪽이 과도하게 학습되어 다른 쪽이 더이상 학습이 진행되지 않는, 학습이 무너지는 현상으로도 이해할 수 있다.
• discriminator를 잘 속이는 것이 곧 좋은 성능을 의미하므로, 만들어지는 이미지의 다양성이 부족하더라도 discrimator을 잘 속이는 방향으로 generator이 이미지를 만들어내는 것이다.
• 이를 해결하기 위해 GAN의 architecture을 개선하고 loss function을 다양하게 조정하는 연구가 활발히 진행되었다.
  • Architecture: SAGAN, StyleGAN ...
  • Loss function: WGAN ...
• GAN이라는 framework를 가장 처음으로 제시했다는 점에서 의미가 있는 논문이지만, 이후에 Generative model들은 빠르게, 그리고 많이 변화해왔다.
• 흥미가 있다면 GAN에 대해 후속 논문들을 읽어보는 것을 추천한다.