데이터 출처 : https://www.kaggle.com/datasets/parulpandey/palmer-archipelago-antarctica-penguin-data
해당 데이터셋(penguins_size.csv)을 살펴보면, 펭귄 각각에 대해서 펭귄의 부리의 길이, 너비, 날개 길이, 종, 사는 지역(섬), 성별 등의 정보가 담겨있는 걸 확인할 수 있다. 이 데이터셋을 바탕으로 펭귄 몸무게 예측을 위한 다중 선형 회귀 모델을 만들어보았다.
1. EDA 및 전처리
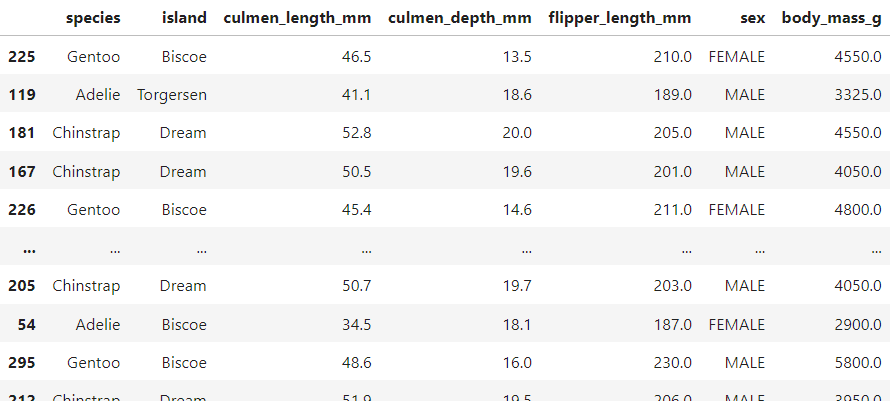
데이터셋은 대충 이렇게 생겼다.
species : 펭귄 종. Adelie(아델리), Chinstrap(턱끈), Gentoo(젠투)
island : 펭귄이 서식하는 섬. Biscoe, Dream, Torgerson
sex : 펭귄 성별. FEMALE(암컷), MALE(수컷)
culmen_length_mm : 부리 길이. 단위 mm.
culmen_depth_mm : 부리 깊이. 단위 mm.
flipper_length_mm : 날개 길이. 단위 mm.
body_mass_g : 몸무게. 단위 g.
결측값이 있는 행은 과감히 제거해줬고,
sex열에 '.'값(이상값)이 하나 있어서 그 행도 제거해줬다.
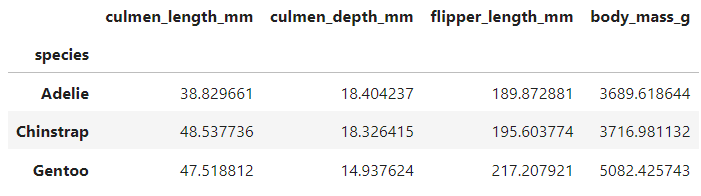
species 혹은 island 혹은 sex에 따라 네 가지 수치형 변수가 어떻게 차이나는지 groupby를 통해 확인해봤다.
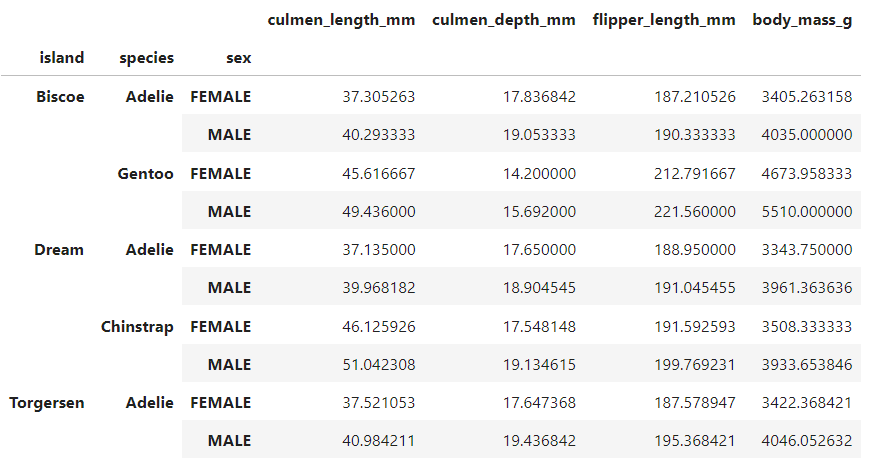
표를 통해서 알 수 있는 것은 크게 두 가지이다.
1) 모든 수치에 있어서 MALE 집단 평균이 FEMALE 집단 평균보다 높다.
2) 모든 섬에 다 데이터가 있는 아델리 펭귄과는 다르게 젠투 펭귄과 턱끈 펭귄은 특정 섬의 데이터만 존재한다.
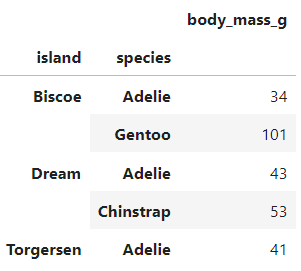
아델리 펭귄의 경우엔, 특정 섬에 몰려있는 것도 아니고 골고루 퍼져있다. 그렇다면 혹시 같은 아델리 펭귄이라도 어느 섬에 살고 있느냐에 따라 수치 상의 차이가 존재하진 않을까? 이를 검정하기 위해 ANOVA 분석을 실시했다.
from scipy.stats import f_oneway
b_adelie = train[(train['island']=='Biscoe')&(train['species']=='Adelie')]
d_adelie = train[(train['island']=='Dream')&(train['species']=='Adelie')]
t_adelie = train[(train['island']=='Torgersen')&(train['species']=='Adelie')]
for column in ['culmen_length_mm', 'culmen_depth_mm', 'flipper_length_mm', 'body_mass_g']:
stat, p = f_oneway(b_adelie.loc[:, column], d_adelie.loc[:, column], t_adelie.loc[:, column])
if p < 0.05:
print(column, '\t차이 O')
else:
print(column, '\t차이 X')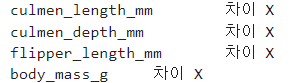
ANOVA 검정 결과, 모든 컬럼에서의 p-value가 0.05보다 높게 나오면서, 서식하는 섬에 따른 차이가 없다는 결과가 나왔다. 만약 모든 섬에 모든 종류의 펭귄이 골고루 분포해있는데 섬에 따른 수치값들이 차이가 났다면 그건 섬의 특성에 따른 차이라고 예측해볼 수 있었겠지만, 지금 같은 경우엔, 특정 펭귄이 특정 섬에 몰려있는 양상이므로, 종의 특성이 반영된, 그것도 아델리 펭귄의 존재로 다소 오염되어 반영된 결과일 뿐, 섬에 따른 특성은 '알 수 없다'고 할 수 있겠다.
종의 특성이 반영된 island 변수를 쓸지, 종 그 자체인 species 변수를 쓸지 양자 택일을 해야한다면 당연히 species를 고르는 게 맞다. 이 두 변수는 게다가 높은 상관관계도 예상되므로, island 변수를 제거해주기로 한다.
그럼 종에 따른 수치값들의 차이는 어떠한지 보자. 날개 길이를 보면, 몸무게의 양상과 같이 가는 걸 확인해볼 수 있을 것이다. 그런데 부리의 경우 그 양상이 조금 다르다. 부리 길이에 있어선 아델리 펭귄이 너무 짧은지, 턱끈 펭귄이 긴 건지 혼란스럽고, 부리 깊이에 있어선 젠투 펭귄이 두 펭귄에 비해 작은 걸 확인할 수 있을 것이다. 즉, 우리가 변수로 사용할 몸무게의 양상과 비교해봤을 때, 세 변수가 각각의 특징적인 양상을 보인다는 것이다. 즉, 비록 어느정도 상관이 있어 보여도 세 변수 중 하나를 제거하는 건 좋지 않은 선택으로 사료된다는 것이다.
여기까지 요약하면,
1) island 변수 안 씀.
2) 수치형 변수는 다 씀.
이렇게 해볼 수 있겠다.
2. 다중 회귀 분석
island 변수를 제외한 두 범주형 변수를 원핫 인코딩 해준 후, 바로 회귀 분석을 돌려주자.
import statsmodels.api as sm
def train_linear_regression(X, y):
X_constant = sm.add_constant(X, has_constant="add")
model = sm.OLS(y, X_constant)
results = model.fit()
return results
X = train.drop(columns=['body_mass_g', 'island_Dream', 'island_Torgersen'])
y = train['body_mass_g']
results = train_linear_regression(X, y)
results.summary()1) 전체적인 요약 표
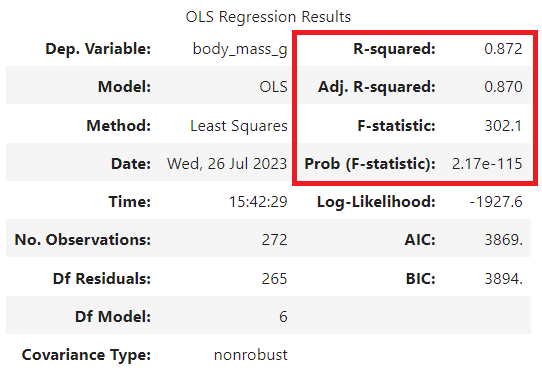
해당 표에선 R2 스코어(R-squared) 값이 어느 정도인지, F값이 유의미한지 정도만 우선 살펴보자. R2 스코어의 경우, SSR에서 SST을 나눈 값으로 계산이 되는데, 이게 도대체 무슨 개념인지는 다른 글을 참고해주고, 0.6보다 높으면 보통 괜찮은 수치라고 본다는 것만 알아두고 가자. 0.872네? 높군! F값이 유의미한지 확인하려면 Prob(F-statistic) 값이 0.05보다 작은지를 확인하면 된다. e-115는 10의 -115승이라는 뜻이다. 2.17에 10의 -115승을 곱한 값. 매우 작군! Log-Likelihood나 AIC, BIC는 변수 선택 상황 등에서 쓰이는 수치인데 지금은 다루지 않겠다.
2) 변수 각각의 회귀 계수 표
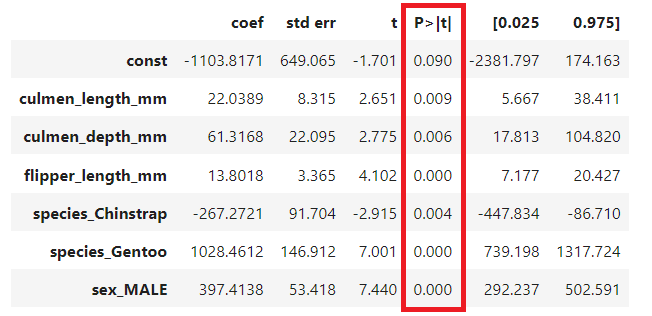
변수 각각에 대해서 회귀 계수를 구하고, 그에 대해서 t값을 구한 후, 해당 t값이 해당 t분포 상에서 유의미한 위치에 분포한가를 확인하면 된다. 대충 P > |t| 값이 0.05보다 작은지만 확인하면 된다는 뜻이다. 만약 여기서 0.05보다 높은 변수가 있을 경우, 보통은 그 변수를 제거해주고 다시 분석을 실행한다. 유의하지 않은 변수가 분석 결과를 오염시킬 수 있기 때문이다. 해당 표에선 모든 변수의 회귀 계수가 유의하다고 나왔으므로, 안심하고 넘어가자.
3) 오차항 관련 표
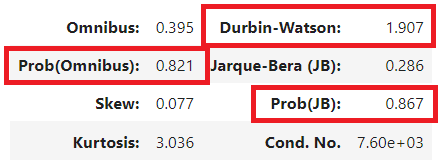
회귀 분석을 실행하기 위해 회귀식의 오차항에 대해서 3가지 가정이 만족되어야 한다. 모든 오차는 등분산이어야 하며, 독립적이어야 하고, 오차항 분포는 정규성을 띄어야 한다는 게 그것이다. 그 중 독립성과 정규성이 성립되었는지 약식으로 해당 표에서 확인해볼 수 있다. Durbin-Watson이 1과 2 사이 있거나 2에 가깝다면, 독립성이 인정된다고 보며, Omnibus, JB의 유의도가 0.05보다 높다면, 정규성이 인정된다고 본다고 한다. 자세한 설명은 다른 글을 참고하시라. 해당 표 상으론, 독립성, 정규성 둘 다 인정된다고 해석해볼 수 있겠다.
3. 모델 적합도 확인
from sklearn.linear_model import Lasso, Ridge, LinearRegression
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error
models = [
("multiple linear regression", LinearRegression()),
("lasso regression", Lasso(alpha=2)),
("ridge regression", Ridge(alpha=2)),
]
test_X = test.drop(columns=['body_mass_g', 'island_Dream', 'island_Torgersen'])
test_y = test['body_mass_g']
for name, model in models:
model.fit(X, y)
y_pred = model.predict(test_X)
print(name)
print('r2 :\t', r2_score(test_y, y_pred))
print('rmse :\t', mean_squared_error(test_y, y_pred)** 0.5)
print('mae :\t', mean_absolute_error(test_y, y_pred))
print('---')선형 회귀 모델을 만드는 데에 가장 일반적으로 쓰이는 함수는 sklearn.linear_model 라이브러리의 LinearRegression이다. 이 함수와, 변수 간의 스케일 차이로 인한 왜곡을 방지하기 위해 고안된 선형 회귀 함수 모델인 Lasso, Ridge 함수를 사용해서도 모델을 만들어보자.
train 데이터를 통해 모델을 학습시킨 후, test의 독립변수를 토대로 종속변수(몸무게)를 예측하고, 해당 예측이 잘 들어맞았는지, R2, RMSE, MAE 스코어를 확인해보겠다. R2 스코어는 앞에서 얼레벌레 넘어가서 알 거고, RMSE, MAE 수치가 등장했는데, 이 두 수치는 회귀 모델의 예측이 얼마나 잘 되었는지를 실제값과 예측값의 차이, 즉 오차가 얼마나 적은지로 판단해보는 수치라는 것만 알아두자. RMSE는 오차값들을 모두 제곱해서 더한 다음 루트를 씌운 값이며, MAE는 오차값들에 절대값을 씌운 후 모두 더해준 갑싱다. 즉, R2는 높은 게 좋고, RMSE, MAE는 낮은 게 좋다 정도로 이해하고 넘어가자는 뜻이다.

결과는 이렇듯 '꽤 잘' 나왔다. 앞서 확인한 train 세트의 R2 스코어가 약 0.87이었는데, 그것과 상당히 비슷한 R2 스코어가 나왔다. 만약 train 세트에 회귀식이 과적합되었다면, test 세트의 예측력이 많이 떨어져 R2 스코어도 큰 폭으로 떨어졌을 것인데 말이다. 그런데 한편으로 RMSE가 200 몇인데 높은 거 아니냐고 생각해볼 수 있을 것이다. RMSE나 MAE는 종속 변수의 스케일이 어느 정도인지를 봐야한다. 종속 변수의 범위가 예를 들어 -100에서 100인데 200 몇의 에러가 발생했다면, 이건 확실히 큰 에러가 발생하고 있다고 할 수 있지만, -10000에서 10000이라면 그 안에서 200은 그렇게 큰 에러가 아니다. 참고로 해당 회귀 분석에서 종속 변수의 평균값은 약 4151.09이다. 약 5% 정도의 에러값이 발생했다는 뜻이니, '꽤 잘' 나온 수치임을 알 수 있다.
모델을 제안한다면, R2 스코어도 다른 모델들보다 근소하지만 높고, 역시 RMSE나 MAE도 근소하지만 낮은 LASSO 회귀 모델을 제안해볼 수 있을 것이다. LASSO 회귀 모델로 펭귄의 몸무게를 예측해보세요! 라고 말이다.
4. 심화
변수 간의 상관관계를 확인해보자.
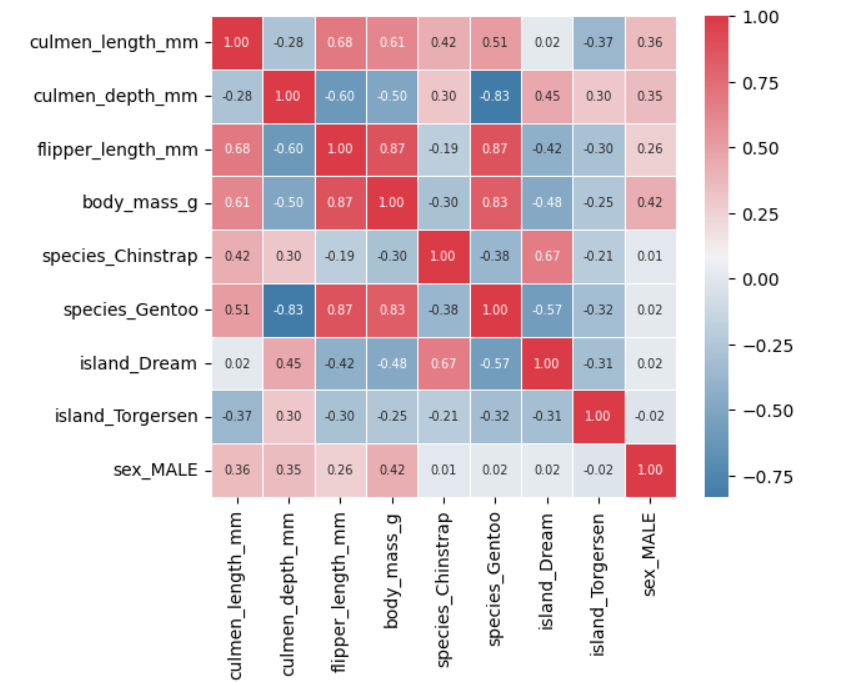
모든 변수에 대해서 절대값 수치가 대체로 높은 변수들이 보이는가(flipper_length_mm 등)? 절대값 수치가 0.8을 넘어가는 조합들이 보이는가? 그렇다면 우린 다중 공선성이 존재하지 않는지 의심해볼 수 있다. 서로 비슷한 얘기를 하고 있는 변수가 같이 있다면, 해당 얘기가 부풀려져 있을 가능성이 있다는 것이다. 다중 공선성은 EDA 과정에서 했던 것처럼 도메인 지식을 활용해서도 확인해볼 수 있겠지만, VIF라는 값을 통해서도 확인해볼 수 있다.
from statsmodels.stats.outliers_influence import variance_inflation_factor
def check_multi_colinearity(X):
vif = pd.DataFrame()
vif["Features"] = X.columns
vif["VIF"] = [variance_inflation_factor(X.values, i) for i in range(len(X.columns))]
vif = vif.sort_values(by="VIF", ascending=False)
return vif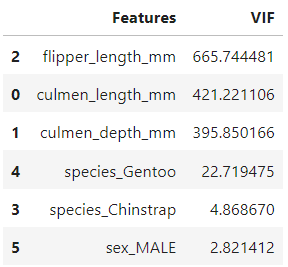
VIF 값이 10이상이면, 보통 다중 공선성을 의심해볼 수 있다고 한다. 다중 공선성이 의심되는 값이 나왔다면, 가장 높은 값을 가진 변수부터 하나씩 지워나가며 모든 변수의 VIF 값이 10 밑으로 떨어질 때까지 이 과정을 반복하면 된다고 한다. 그렇게 해서 변수를 지우면 flipper_length_mm와 culmen_length_mm 변수를 지우면 된다는 결과가 나온다. 이 결과를 바탕으로 선형 회귀 분석을 돌려보면, 좋은 결과가 나온다는 것인데...

결과는 영 신통치 않았다. r2는 낮아지고, 에러는 높아졌다. 즉, 수치상으로 다중 공선성이 의심된다고 해도, 논리상 모든 변수가 엄연히 다른 이야기를 하고 있다면, 변수 삭제를 굳이 하지 않는 선택지도 있다는 것이다. 게다가 이 VIF는 변수들의 스케일에도 영향을 받는다. 스케일이 클수록 높은 값이 나올 수 있다는 것이다.
5. 결론
펭귄의 몸무게를 예측해볼테니, 펭귄 부리의 길이, 깊이, 날개의 길이, 종, 성별만 알려주라.

