Rain in Austraila

데이터 출처 : Rain in Australia

호주 전역의 약 10년 간의 날짜 기록을 모아둔 데이터셋이다. 이 데이터를 이용하여 다음날 비가 왔는지 여부(RainTomorrow : 1, 0)를 예측하는 모델을 만들어보고자 한다. 라벨링이 되어 있고, 종속 변수가 범주형 변수이므로 로지스틱 회귀모델을 이용해보기로 한다.

1. EDA 및 전처리

- 결측치 제거

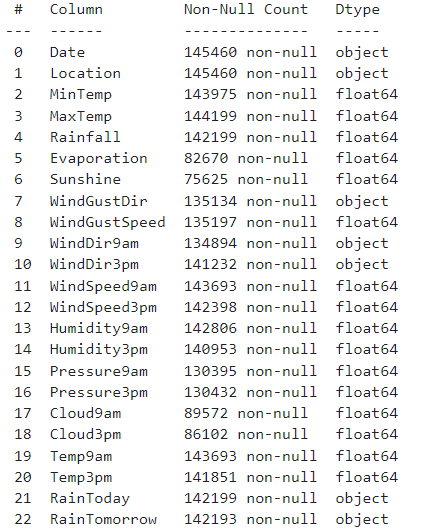
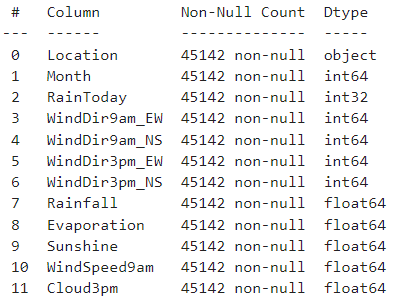
데이터의 상태가 심상치 않음을 알 수 있다. 결측치가 너무 많다. 이렇게 결측치가 많아서야 섣불리 결측치를 잘못 조정했다간 왜곡만 커질 심산이 높아보인다. 결측치를 모두 제거해도 충분히 많은 양의 데이터를 확보할 수 있으니, 모두 제거해주기로 한다.

df.dropna()

- 칼럼 타입 변경

먼저 Date 칼럼의 타입을 Date 타입으로 바꿔주고, Month 칼럼을 새로 추출해주자.

df['Date'] = pd.to_datetime(df['Date'])
df['Month'] = df['Date'].dt.month
df = df.drop(columns=['Date'])

그리고 RainToday, RainTomorrow의 타입을 1, 0 형태인 int 타입으로 라벨 인코딩해주자.

le = LabelEncoder()
df['RainToday'] = le.fit_transform(df['RainToday'])
df['RainTomorrow'] = le.fit_transform(df['RainTomorrow'])

풍향 정보를 담고 있는 'WindGustDir', 'WindDir9am', 'WindDir3pm' 열을 처리해줘야 하는데, 일괄적으로 라벨 인코딩이나 원핫 인코딩 처리를 하기엔, 각각의 범주의 개수가 16개로 너무 많다.

16방위로 표기된 풍향 정보를 어떻게 숫자로 표기해볼 수 있을까? 위 그림에서 방위가 적혀있는 위치를 일종의 x, y 좌표상에 찍혀있는 점이라고 생각해보면 어떨까? 가운데가 (0, 0)의 위치라면, E(동)의 위치는 (4,0), SSE(남남동)의 위치는 (1, -3) 라고 생각해볼 수 있을 것이다. EW, NS 칼럼을 새로 만들어서 각각 x, y 위치값을 담아주기로 한다.

# mapping_ew_dir, mapping_ns_dir 함수를 직접 만들어주자.
for col in [x for x in df.columns if 'Dir' in x]:
    df[f'{col}_EW'] = df[col].apply(mapping_ew_dir)
    df[f'{col}_NS'] = df[col].apply(mapping_ns_dir)
    df = df.drop(columns=[col])

- train, test 분리

지도 학습을 위해 데이터셋을 train, test로 분리해주자.

X = df.drop(["RainTomorrow"], axis=1)
y = df["RainTomorrow"]
x_train, x_test, y_train, y_test = \
train_test_split(X, y, train_size=0.8, random_state=1234)

2. 변수 선택

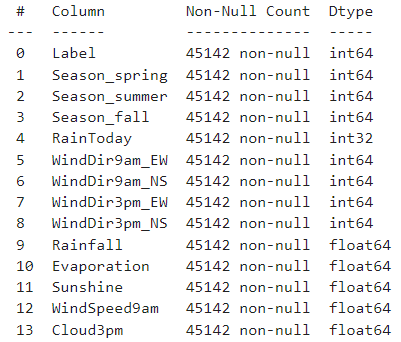
우선 코딩을 좀 더 원활하게 하고, 한눈에 파악도 용이하게 하기 위해 범주형 변수를 앞쪽에, 연속형 변수를 뒤쪽에 배치해주자. int 타입의 변수는 전부 범주형이고 float 타입의 변수는 전부 연속형이다.

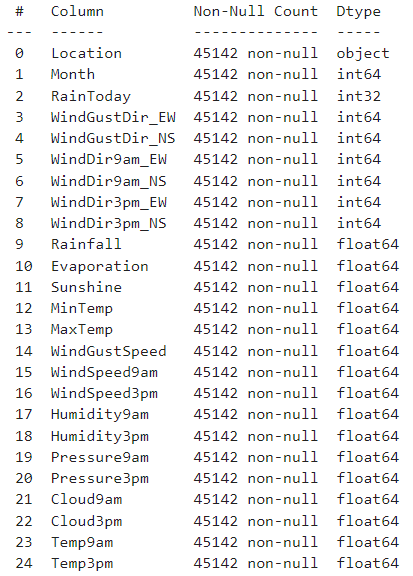
x_train.info()를 해보면 위와 같은 결과가 나올 것이다. 그런데 한눈에 봐도 변수가 너무 많다. 왠지 시간에 따라 나눠져있는 칼럼끼리는 상관도 높아보이고, 다중공선성의 위협이 너무 크게 느껴진다. 변수를 솎아내줄 필요가 있어보이는데 어떻게 해볼 수 있을까? 범주형, 연속형 각각 y_train과의 상관관계를 살펴보자.

- 범주형 변수 상관관계

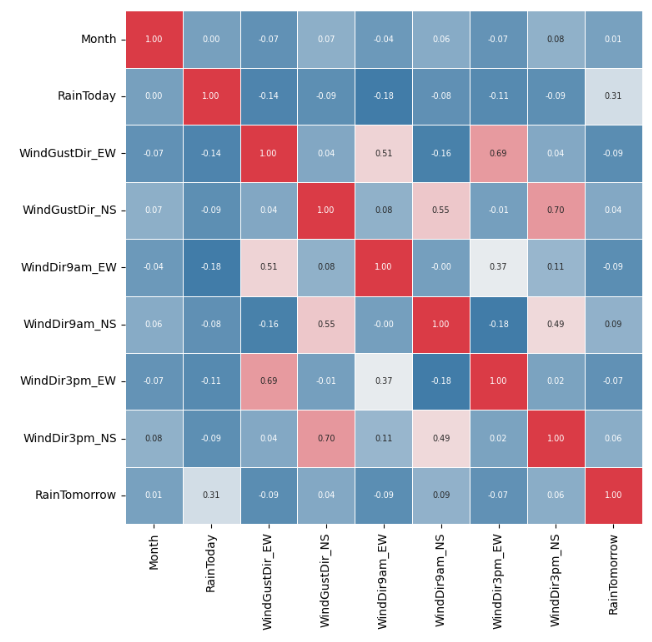
범주형 변수끼리의 상관을 보면, EW는 EW끼리 NS는 NS끼리 상관이 높게 형성되는 걸 볼 수 있다. 특히 Gust와 Dir3pm의 상관은 0.69, 0.70으로 매우 다소 높은 선형적 상관이 있다는 것으로 나타난다. 둘 중 한 카테고리를 지워주면 좋겠는데, 9am과 상관이 더 적은 3pm을 남기고, Gust를 지워주기로 한다.

- 연속형 변수 상관관계

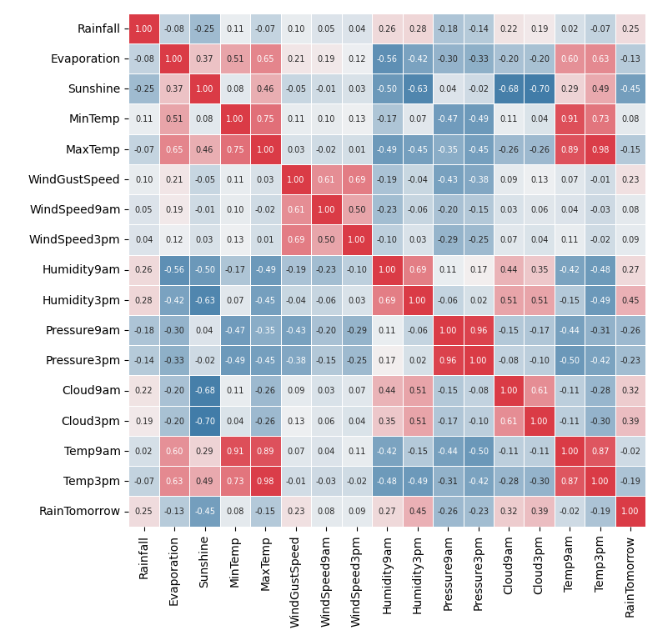
연속형 변수끼리의 상관을 보면, 역시 예상대로 카테고리가 같은 변수끼리 상관이 높게 형성되는 걸 확인할 수 있다. 특히 Temp끼리는 0.9를 넘어가는 수준이다. 일단 먼저 범주형 변수에서 처리해준 것처럼 Gust 카테고리인 WindGustSpeed부터 지워준다. 그리고 9am, 3pm으로 나뉜 변수 중에선 RainTomorrow와의 상관관계가 더 낮게 형성된 걸 지워주기로 한다. 그런데 특별히 다른 변수와 높은 상관관계가 발견되는 쪽이 있다면 그 쪽을 지워주기로 하자.

Temp 카테고리 변수인 MinTemp, MaxTemp, Temp9am, Temp3pm 끼리는 다 서로 상관이 너무 높게 나오고 있다. 그러니 이 중 하나만 남기기로 하자. 여기선 RainTomorrow와 상관관계가 높게 나오는 Temp3pm을 남긴다.

이와 같은 방식으로 WindSpeed, Humidity, Pressure는 9am 변수를, Cloud는 3pm 변수를 남기기로 한다.

- 변수 선택 후 종합 상관관계

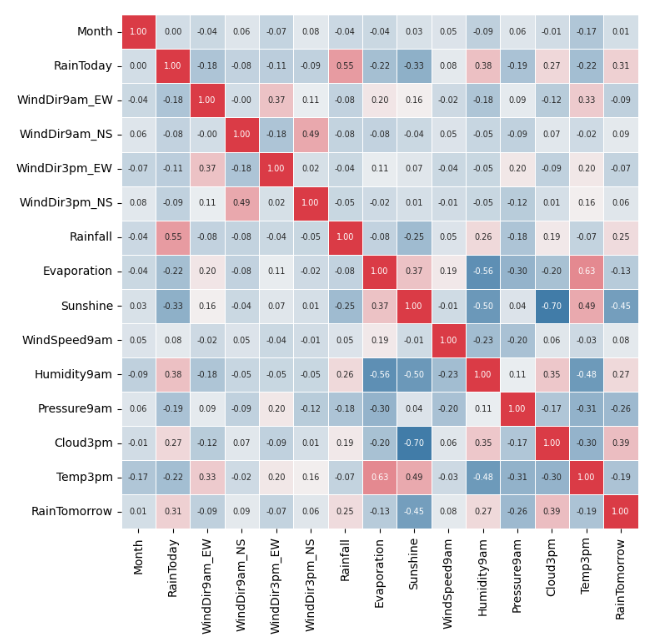
여전히 연속형 변수끼리 중에선 높은 상관을 보이는 조합이 보이지만, 카테고리 정리가 어느 정도 되었으므로, 상관관계를 근거로 한 변수 선택은 여기까지 하기로 한다.

- VIF

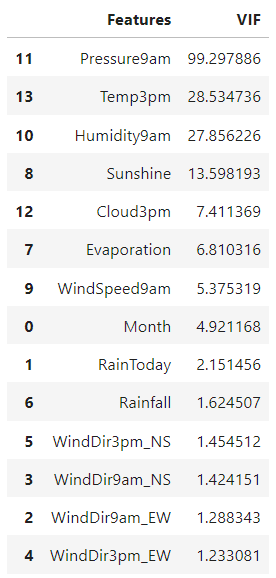
VIF 계수가 10이 넘어가면 해당 변수에 대해서 다중 공선성이 존재한다고 해석할 수 있다고 한다. VIF상으로 나타나는 다중 공선성을 없애려면, 최종적으로 모든 변수가 VIF가 10을 넘지 않는 시점까지 VIF 계수가 가장 높은 변수를 하나하나 지워가면 된다. 여기선 Pressure9am, Temp3pm, Humidity9am 변수를 지워주니 다중 공선성이 사라졌다.

여기까지 12개의 변수를 남기는 것으로 변수 선택을 완료한다.

3. Location, Month 군집화

이제 너무나 거슬렸는데 왜 언급조차 없나 궁금했을 Location 변수를 처리해보자. Location의 값으론 호주 전역에 퍼져있는 49개의 관측소 값이 들어있다. 관측소가 어디냐에 따라 날씨 양상이 달라지는 것은 너무 자명해보이는데, 과연 그렇게까지 다르지 않은 관측소까지 분리해서 알아볼 필요가 있을까? 호주의 행정구역 상으로 6개의 주가 있고 3개의 준주가 있다고 한다. 그러나 이 행정구역은 기후가 기준이 아니기에, 실제 날씨 데이터 값을 기준으로 봤을 때 차이가 적은 지역끼리 묶어주는 방법을 쓰기로 한다. 그 기법으로 '계층적 군집분석' 기법을 활용해보자.

- StandardScaler (정규화)

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()

columns = pd.concat(
	[x_train, y_train],
    axis=1
).groupby(['Location']).mean().columns

index = pd.concat(
	[x_train, y_train],
    axis=1
).groupby(['Location']).mean().index

X = pd.DataFrame(
	scaler.fit_transform(
    	pd.concat(
        	[x_train, y_train],
            axis=1
        ).groupby(['Location']).mean()
    ), 
    columns=columns, 
    index=index

일단 변수마다 스케일이 맞지 않으니 정규화를 해준다. 다음, Location 변수를 기준으로 모든 변수들의 평균을 구한다. 그럼 아래 그림과 같은 표가 만들어진다.

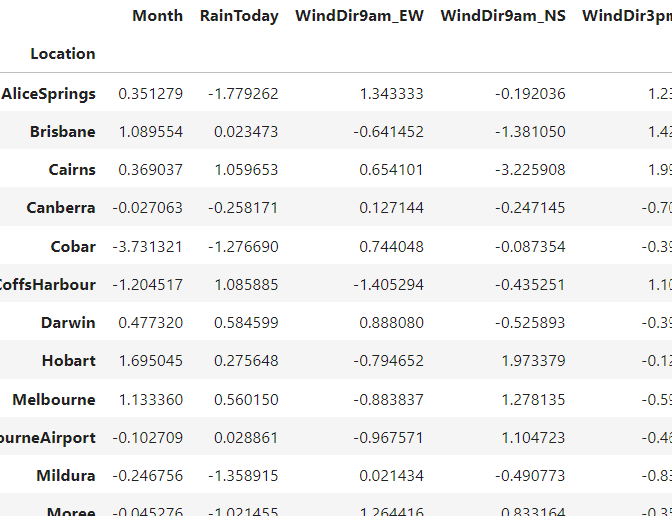
이렇게 표를 계층적 군집분석 코드에 넣어주면 된다. 참 쉽다.

- 덴드로그램

from scipy.cluster import hierarchy as hc
labels = X.index
model = hc.dendrogram(
    hc.linkage(X, method="ward"),
    labels=labels,
    orientation='right'
)
plt.title('Dendrogram')
plt.axvline(7, color="gray", linestyle="--", label="num clusters: 4")
plt.legend()
plt.show()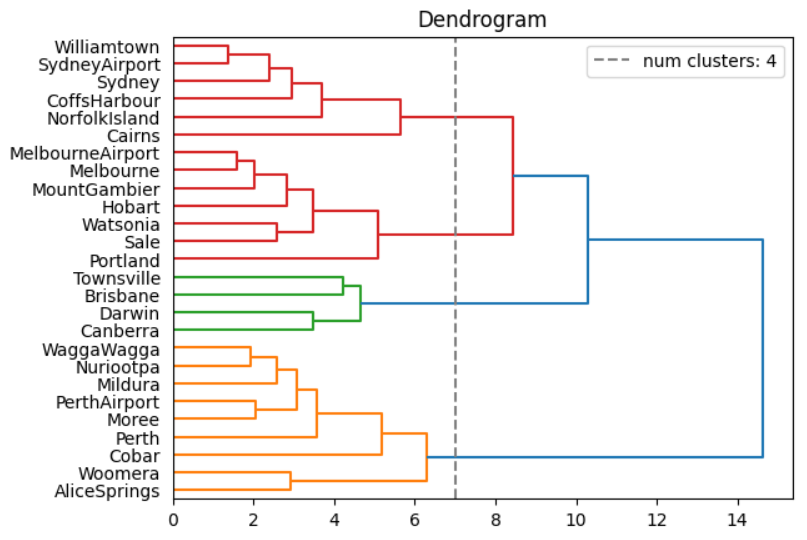

Ward라는 학자가 고안한 Ward 거리 측정법에 따라 각 점들간의 거리를 구하고, 그 거리가 짧은 변수부터 차례대로 군집화해나간 과정을 보여주는 그래프이다. 보통은 '뭔가' 빽빽해지기 직전의 군집수를 최적의 군집수로 파악한다. 여기에선 ward 거리가 7인 선을 기준으로 군집된 집단의 수를 살펴보면 4개의 집단으로 나뉨을 확인할 수 있다.

- 실루엣 계수

from sklearn.metrics import silhouette_score
from sklearn.cluster import AgglomerativeClustering
silhouette_scores = []
for n_cluster in range(2, 8):
    model = AgglomerativeClustering(n_clusters=n_cluster, linkage="ward")
    X_pred = model.fit_predict(X)
    score = silhouette_score(X, X_pred)
    silhouette_scores.append(score)   
plt.bar([x for x in range(2, 8)], silhouette_scores)
plt.title('Silhouette Score')
plt.xlabel('n_cluster')
plt.show()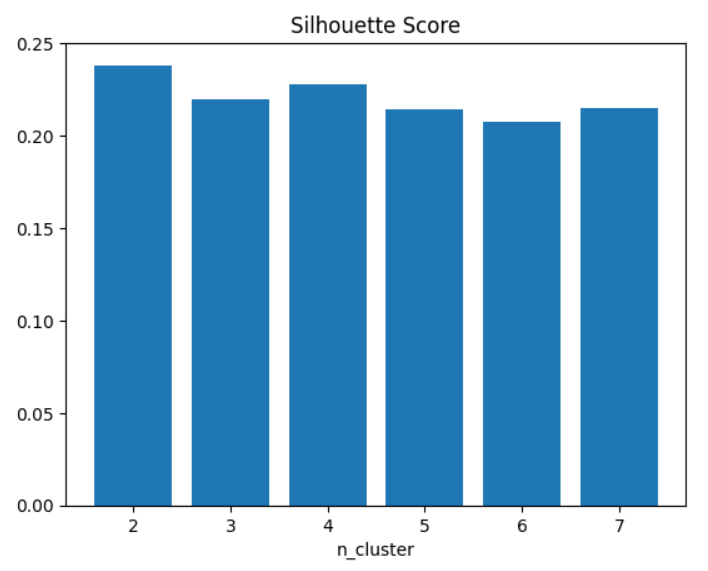

실루엣 계수는 군집수(n_cluster)에 따라 얼마나 집단 간 거리가 떨어져있는지를 알려주는 지표이다. 이 값이 높을수록 각 집단은 상이하다는 뜻이다. 표를 보면 군집의 개수가 2를 제외하곤 4인 경우에 실루엣 계수가 가장 높게 형성됨을 알 수 있다.

- 군집 수 결정

덴드로그램, 실루잇 계수 그래프를 종합하면, 실루엣 계수가 높으면서 각 집단마다 개수가 골고루 분포되게 하기 위해선 네 집단으로 나누는 게 제일 적절하다고 판단할 수 있다. n_cluster를 4로 확정한다.

model = AgglomerativeClustering(n_clusters=4, linkage="ward")
X_pred = model.fit_predict(X)
X['Label'] = X_pred
X['Label'].value_counts()
x_label = X['Label'].reset_index()

x_train = pd.merge(
	x_train.reset_index(), 
    x_label, 
    how='left', 
    on='Location'
).set_index('index')

x_test = pd.merge(
	x_test.reset_index(), 
    x_label, 
    how='left', 
    on='Location'
).set_index('index')

- Month -> Season

Month도 범주의 개수가 12개로 꽤나 많다. 도메인 지식을 활용해 봄, 여름, 가을, 겨울로 만들어주자.

# x_test도 동일
x_train['Season_spring'] = x_train['Month'].apply(
	lambda x: 1 if 3 <= x <= 5 else 0
)
x_train['Season_summer'] = x_train['Month'].apply(
	lambda x: 1 if 6 <= x <= 8 else 0
)
x_train['Season_fall'] = x_train['Month'].apply(
	lambda x: 1 if 9 <= x <= 11 else 0
)

수동 원핫 인코딩을 해주자. winter를 만들지 않은 이유는 세 변수가 다 0이면 winter인 걸 알 수 있기 때문이다. 변수 순서를 정리해주면 독립 변수는 다음과 같다.

4. 오버 샘플링

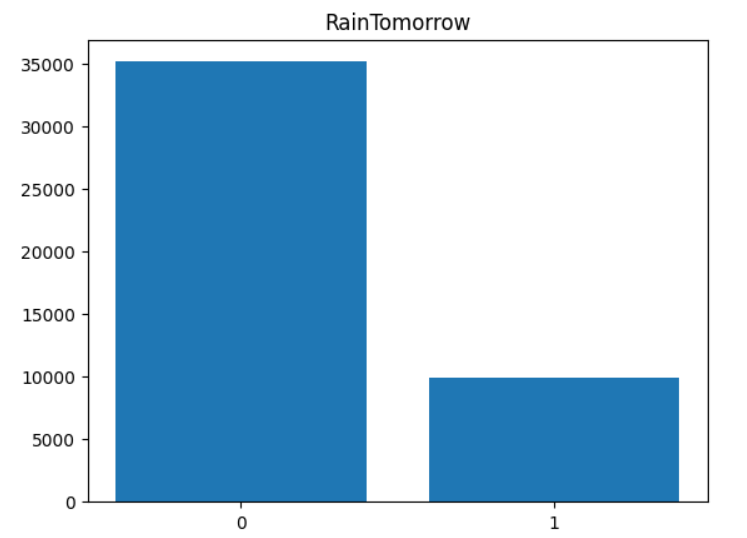
종속 변수 RainTomorrow는 그래프에서 확인할 수 있듯이 불균형 그래프이다. 우리가 날씨를 확인할 때 보통 정확히 알고 싶어하는 건 비가 오냐 마냐이다. 즉, 이제 모델을 만들텐데 실제값이 1일 때 1을 잘 맞혀내는 모델을 만들어야 할 건데, 이렇게 불균형한 모델일 경우, 예측값이 샘플수가 더 많은 0에 쏠릴 심산이 크다. 그런 관계로 1의 샘플수를 증가시켜, 즉, 오버 샘플링을 하여 불균형을 해소해주기로 한다. 방법은 단순하게 했다. 종속 변수가 1인 샘플들을 3배 증가시켜줬다.

train = pd.concat([x_train, y_train], axis=1)
train_1 = train[df['RainTomorrow']==1]
train_0 = train[df['RainTomorrow']==0]
train_over = pd.concat([train_1, train_1, train_1, train_0])
train_over = train_over.reset_index(drop=True)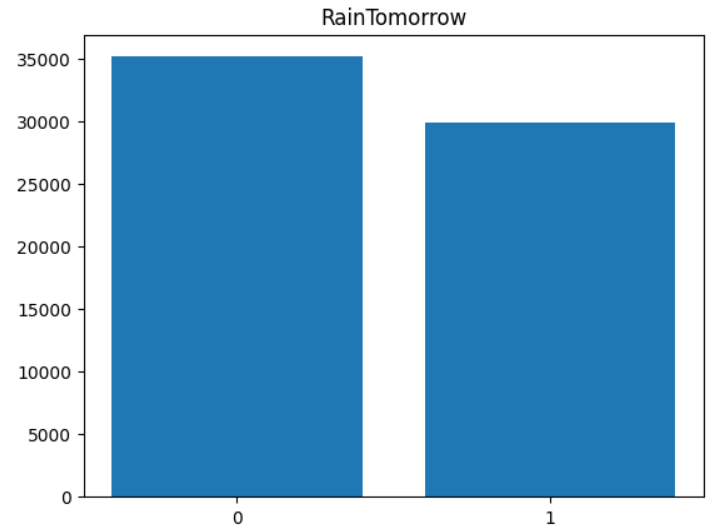

5. 로지스틱 회귀 분석

로지스틱 회귀 분석을 돌린 결과, Evaporation 변수의 회귀 계수가 유의하지 않다고 나와, Evaporation 변수를 제거해주고 다시 돌려주었다. 그 결과는 아래와 같다.

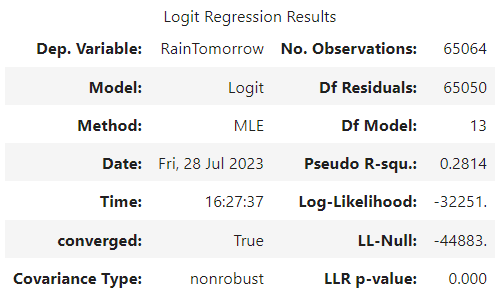
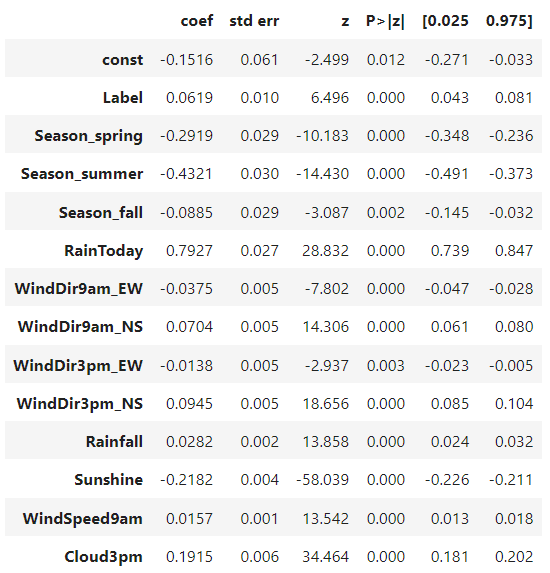
이제 이 모델로 x_test를 예측하고, y_test와 비교하여 얼마나 잘 들어맞았는지 확인해보자.

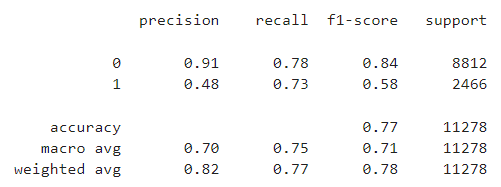
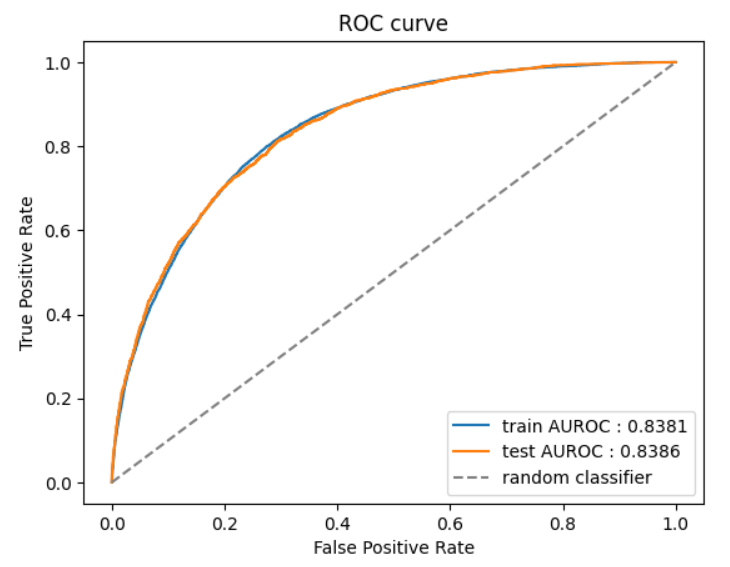
train 자체적으론 accuracy(정확도), recall(재현율), precision(정밀도), f1, roc_auc 수치 모두 골고루 잘 나왔지만, test를 보면 precision 값이 확 떨어졌다는 걸 알 수 있다. 사실 데이터의 불균형을 해소하지 않고 모델을 학습하면 반대의 결과가 나온다. recall이 떨어진다. recall이 떨어진다는 것은 위양성을 걸러내지 못한다는 의미이다. 즉, 비가 올 것임에도 비가 안 올 것이라고 한다는 것이다. 만약 불균형을 해소하지 않은 모델을 사용한다면, 정확도 자체는 더 높을 것이다. 0인 경우는 귀신같이 잘 맞힐 것이기 때문이다. 그러나 우리가 일기예보를 보는 이유는 '비를 피하기 위함'이 더 크다. 즉, recall이 높지 않다면, 그냥 무조건 비가 안 올 것이라고 가정한 경우와 크게 다르지 않을 것이다. 이 문제를 해결하기 위해, 비가 오는 경우에 잘 적합하게 모델을 수정해줬다. 그 영향으로 해가 쨍쨍한 날에도 우산을 들고 갈 가능성이 커지긴 했지만, 쫄딱 비 다 맞는 것보단 괜찮지 않은가? 우산을 양산 대신 쓸 수도 있고.

6. 마치며

아무래도 종국엔 recall, precision 중 양자 택일을 해야 했던 게 아쉬움으로 남는다. 둘 모두 잘 맞힐 수 있다면, 훌륭한 모델이겠지만, 어디 한낱 집에서 컴퓨터 한 대로 모델 만들어서 돌려 본 결과가 더할 나위 없이 훌륭해버리면 기상청이 있을 이유가 없지 않겠는가. 그리고 도메인 지식이 더 충분히 있었다면 변수 선택에 있어서 논리적 타당성을 더할 수 있었을 건데, 이 점도 아쉬움으로 남는다.