Paper : Robust Dynamic Radiance Fields

Abstract

배경

• 기존의 dynamic radiance field reconstruction 방법은 정확한 카메라 포즈를 SfM(Structure from Motion) 알고리즘에 의해 안정적으로 추정할 수 있다고 가정
• 그러나 SfM 알고리즘은 매우 동적인 물체, 잘못된 질감의 표면, 회전하는 카메라 움직임이 있는 비디오에서 잘못된 pose를 생성하기 때문에 신뢰할 수 없음

제안

• 카메라 매개 변수(pose 및 focal length)와 함께 static 및 dynamic radiance field를 공동으로 추정하여 이 robustness 문제 해결

결과

• state-of-the-art dynamic view synthesis 방법에 비해 유리한 성능을 보임

2. Related Work

Dynamic view synthesis

최근 동적 장면에서 새로운 뷰를 재구성하고 합성하는 여러 연구가 진행되었다.

• 인체에 초점을 맞추고(Humannerf), RGBD 데이터를 사용하고(Fusion4D), sparse geometry를 재구성하거나, 입력 뷰 간의 minimal stereoscopic disparity transition 생성
• hand-crafted prior을 사용하여 동적 장면을 piece-wise rigid part로 분해

많은 시스템은 복잡한 기하학적 구조를 가진 장면을 처리할 수 없으며, 대신 interactive view manipulation을 제공하기 위해 multi-view 및 time-synchronized 비디오를 입력으로 요구한다.

Novel view synthesis of dynamic scenes with globally coherent depths from a monocular camera는 단일 뷰 및 멀티뷰 스테레오의 깊이를 사용하여 명시적 깊이 기반 3D 와핑을 사용하여 단일 비디오에서 동적 장면의 새로운 뷰를 합성했다.

최근 연구는 동적 장면을 처리하도록 NeRF를 확장한다.

• TiNeuVox, Open4D, Neural Scene Flow Fields, Nerfies, Hypernerf, D-nerf, Non-Rigid Neural Radiance Fields, Space-time neural irradiance fields for free-viewpoint video

이러한 시공간 합성 결과는 인상적이지만, 이러한 기술은 정확한 camera pose 입력에 의존한다. 이는 즉슨, COLMAP 또는 SfM 시스템을 통해 추정이 실패하는 어려운 장면에는 부정확한 결과를 초래한다. 따라서 본 연구의 접근 방식은 known camera pose 없이 복잡한 동적 시나리오를 처리할 수 있다.

Visual odometry and camera pose estimation

이미지 모음에서 visual odometry는 3D camera pose를 추정한다.

• photometric consistency을 극대화하는 직접 방법
• 수동으로 생성되거나 학습된 feature에 의존하는 feature 기반 방법

Visual odometry
로봇 공학 및 컴퓨터 비전에서 카메라의 입력을 받아 객체(차량,인간,로봇)의 위치와 방향을 추정하는 과정

자체 감독 이미지 재구성 손실은 최근 학습 기반 시스템에서 시각적 오도메트리 [2, 6, 26, 35, 70, 77, 80, 81, 83, 84]를 다루기 위해 사용되었다.

무심코 캡처한 비디오에서 카메라 포즈를 추정하는 것은 여전히 어려운 작업이다. NeRF 기반 기술은 정적 시퀀스로 제한되지만 최적화를 위해 신경 3D 표현과 카메라 포즈를 결합하도록 제안되었다. 따라서 본 연구의 시스템은 camera pose를 동시에 최적화하고 동적 객체 모델을 모델링한다.

3. Method

3.1. Preliminaries

NeRF

Neural radiance fields(NeRF)는 $\Theta$에 의해 파라미터화된 implicit MLP로 정적 3D 장면을 나타내며 3D 위치 $(x, y, z)$ 및 viewing direction $(θ, ϕ)$을 해당 컬러 $\mathbf c$ 및 밀도 $σ$에 매핑한다:

카메라 원점에서 방출되는 ray에 따라 볼륨 렌더링을 적용하여 픽셀 색상을 계산할 수 있다:

• $δ(i)$ : ray에 따라 연속되는 두 샘플 포인트 사이의 거리
• $N$ : 각 ray 위의 샘플의 수
• $T(i)$ : 누적된 투명도

볼륨 렌더링 절차는 미분 가능하므로 렌더링된 색상 $\hat\mathbf C$와 실측 색상 $\mathbf C$ 사이의 reconstruction error를 최소화하여 radiance field를 최적화할 수 있다:

Explicit neural voxel radiance fields

NeRF 기반 방법은 저장 효율성을 위해 MLP와 같은 implicit representation으로 장면을 모델링한다. 그러나 이 방법은 훈련하는 속도가 매우 느리다. 이 단점을 극복하기 위해 최근 연구는 explicit voxel로 radiance field를 모델링할 것을 제안한다.

이 방법은 매핑 함수를 voxel grid로 대체하고 voxel에서 샘플링된 feature를 직접 최적화한다. 이 방법은 일반적으로 작은 MLP를 사용하여 view-dependent 효과를 처리한다. MLP를 적게 사용으로써 훈련 시간이 며칠에서 몇 시간으로 단축된다. 본 연구는 explicit representation을 활용한다.

3.2. Method Overview

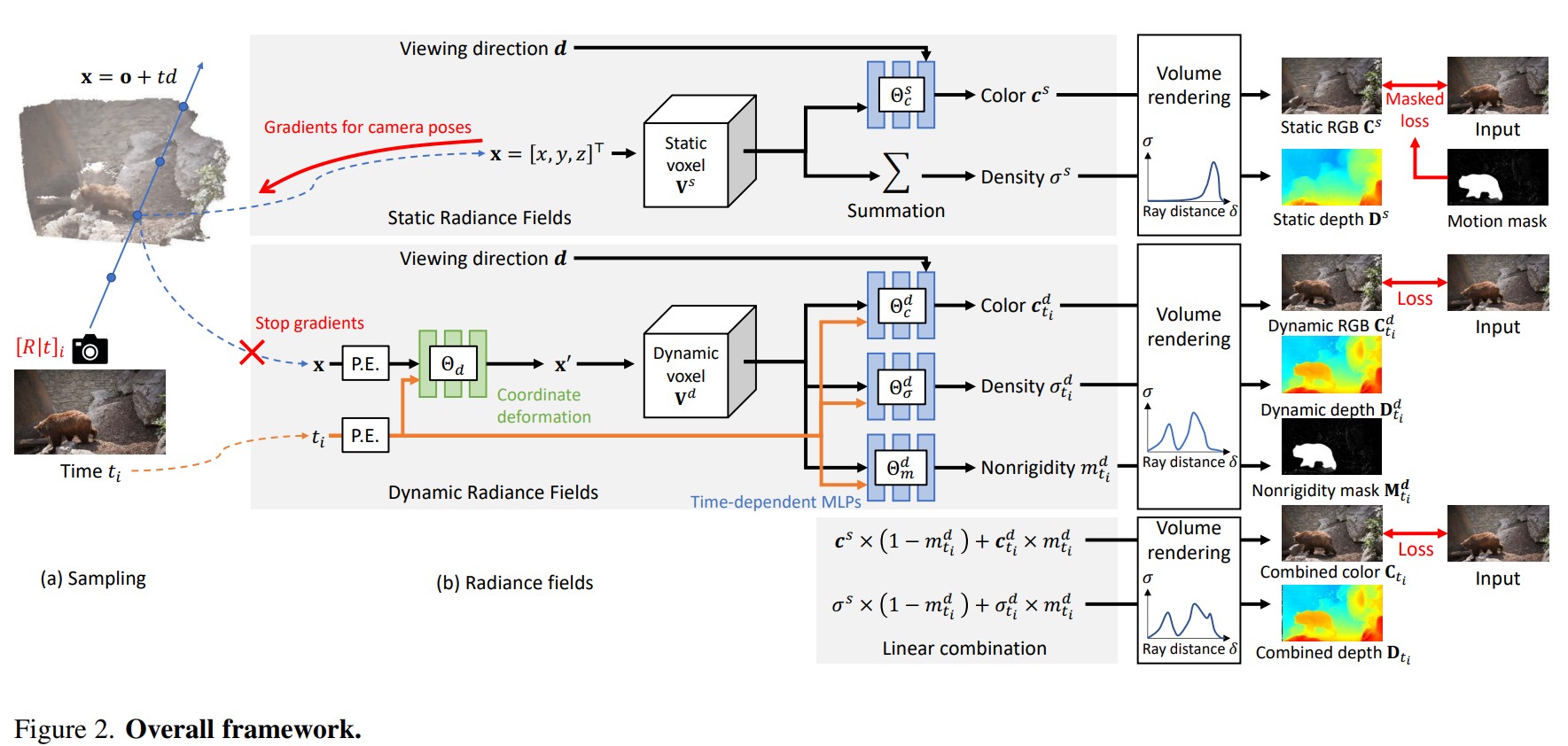
$N$개의 프레임으로 입력 비디오 시퀀스가 주어지면, camera pose, focal length, static 및 dynamic radiance field를 공동으로 최적화한다. 정적 부분과 동적 부분을 각각 explicit neural voxel $\mathbf V^s$와 $\mathbf V^d$로 표현한다.

Static radiance field

static radiance field는 정적 장면을 재구성하고 camera pose와 focal length를 추정하는 역할을 한다.

1. 샘플링된 좌표 $(x, y, z)$와 viewing direction $\mathbf d$를 모두 입력으로 받아 밀도 $σ^s$와 색상 $c^s$를 예측한다.
2. 정적 부분의 밀도는 시간과 viewing direction에 invariant하므로 쿼리된 feature의 합을 밀도로 사용한다(MLP를 사용하는 대신).
3. 정적 영역에 대한 loss만 계산하며 계산된 gradient는 static voxel field와 MLP뿐만 아니라 카메라 파라미터에도 역방향으로 전달한다.

Dynamic radiance field

dynamic radiance field는 비디오의 장면 역학(일반적으로 움직이는 물체에 의해 발생)을 모델링한다.

1. 샘플링된 좌표와 시간 $t$를 사용하여 canonical space에서 deformed coordinates $(x ′, y ′, z′)$를 얻는다.
2. dynamic voxel field에서 변형된 좌표를 사용하여 feature를 쿼리하고 time index와 함께 feature를 time-dependent 얕은 MLP에 전달하여 동적 부분의 색상 $c^d$, 밀도 $σ^d$ 및 nonrigidity $m^d$를 얻는다.

마지막으로 볼륨 렌더링 후 정적 및 동적 부분에서 RGB image $\mathbf C^{\{s,d\}}$와 깊이 맵 $\mathbf D^{\{s,d\}}$를 nonrigidity mask $\mathbf M^d$와 함께 얻을 수 있다. 이후 프레임별 reconstruction loss를 계산한다. 이때, 프레임별 loss만 포함한다.

3.3. Camera Pose Estimation

Motion mask generation

비디오에서 동적 영역을 제외하면 카메라 포즈 추정이 수월해진다. 기존 방법은 Mask R-CNN과 같은 기성 instance segmentation 방법을 활용하여 공통 이동 객체를 마스킹하곤 했다. 그러나 입력 비디오에서 물이 흐르거나 나무가 흔들리는 것과 같이 활동성이 많은 객체는 감지/분할하기 어렵다.

따라서 Mask R-CNN의 mask 외에도 연속 프레임의 optical flow을 사용하여 기본 행렬을 추정한다. 그런 다음 Sampson distance(각 픽셀에서 추정된 epipolar line까지의 거리)를 계산하고 임계값을 지정하여 binary motion mask를 얻는다. 마지막으로 Mask R-CNN과 epipolar distance 임계값의 결과를 결합하여 최종 motion mask를 얻는다.

Coarse-to-fine static scene reconstruction

먼저 camera pose와 함께 static radiance field를 재구성한다. 6D camera pose $[R|t]_i, i ∈ [1..N]$ 및 모든 입력 프레임이 동시에 공유하는 focal length $f$를 공동으로 최적화한다. 기존 포즈 추정 방법과 유사하게, coarse-to-fine 방법으로 static scene representation을 최적화한다. 이 방법은 energy surface가 더 부드러워지기(?) 때문에 camera pose 추정에 필수적이다. 따라서 optimizer는 sub-optimal solution에 갇힐 가능성이 적다(그림 4(a) vs. 그림 4(d)).

Late viewing direction conditioning

주된 감독은 photometric consistency loss이기 때문에, 최적화는 neural voxel을 우회하고(?) viewing direction에서 출력 샘플 색상까지의 매핑 함수를 직접 학습할 수 있다. 따라서,색상 MLP의 마지막 레이어에서만 viewing direction을 융합하도록 선택한다. 이 설계는 scene geometry뿐만 아니라 camera pose도 재구성하고 있기 때문에 매우 중요하다.

Late viewing direction 조정 없이 MLP를 최적화함으로써 photometric loss를 최소화하면, 잘못된 camera pose 및 geometry 추정을 초래할 수 있다(그림 4(c)).

Losses

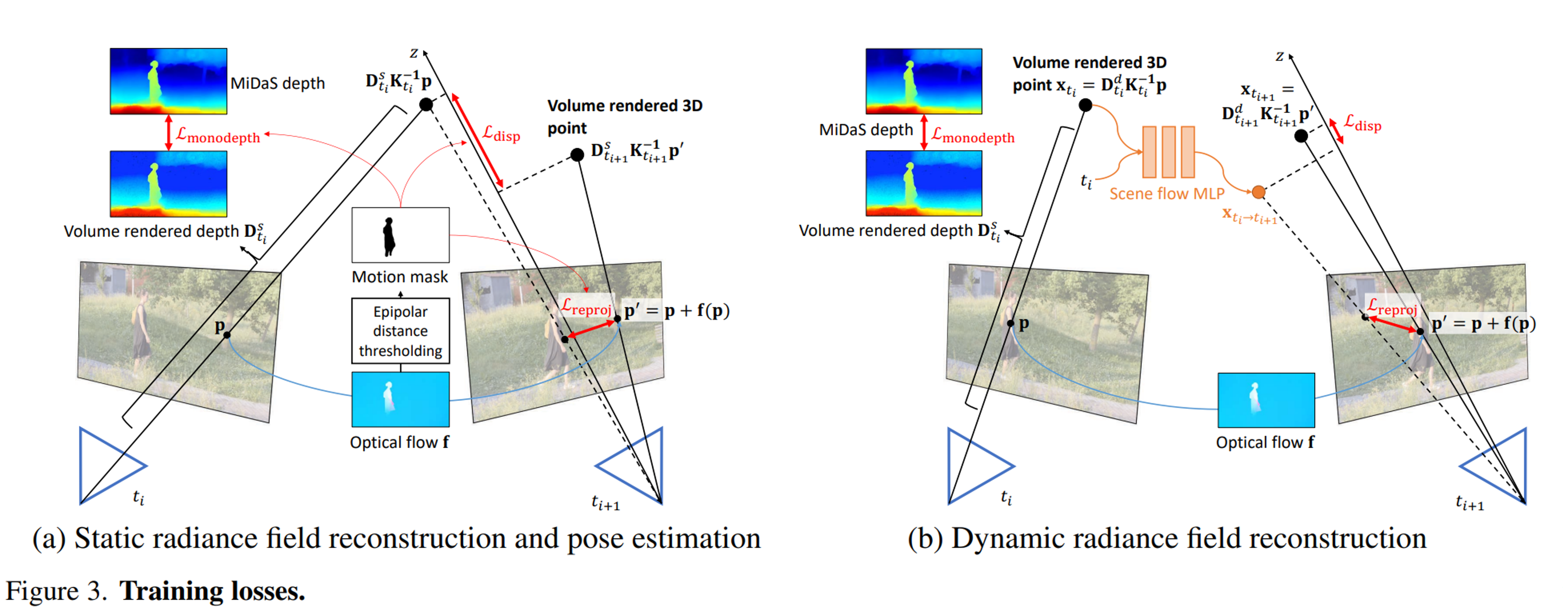
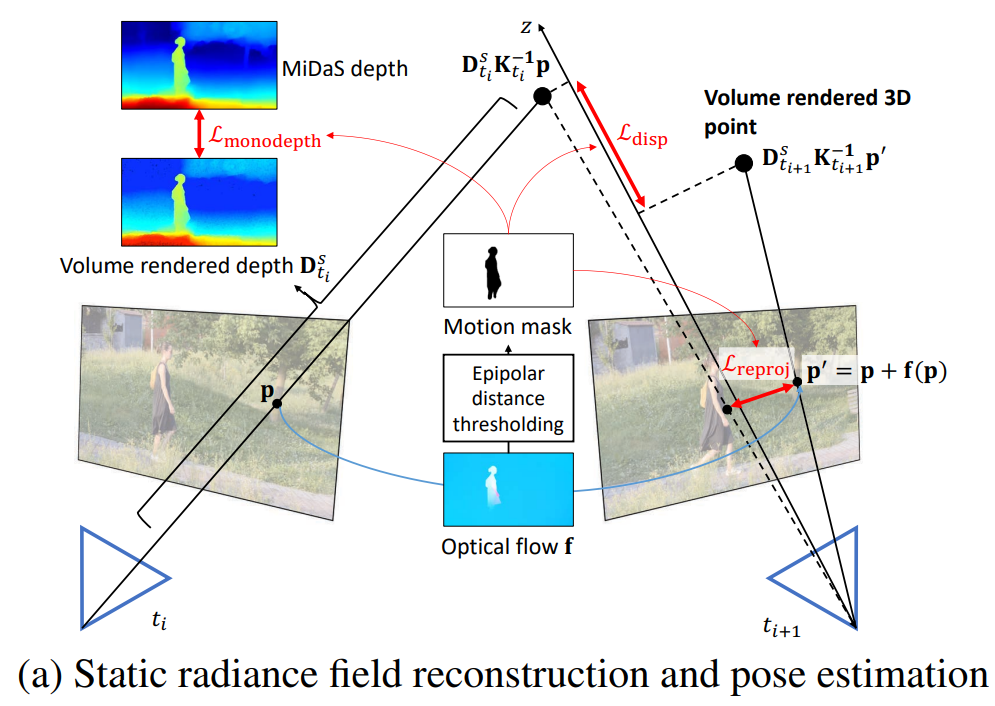
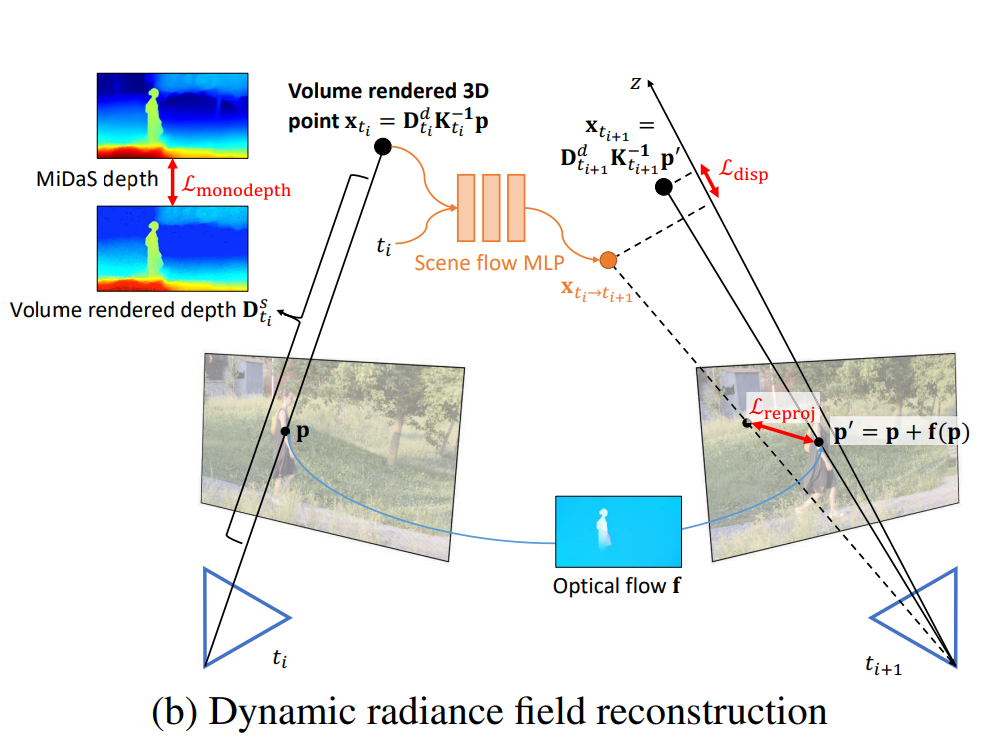
(a) loss 계산에서 동적 영역을 제외하기 위해 motion mask를 사용한다. (b) scene flow MLP를 사용하여 렌더링된 볼륨 3D 포인트의 3D 움직임을 모델링한다.

• Reprojection loss : 3D 볼륨 렌더링 포인트를 이웃 프레임에 투영하여 사전 계산된 flow와 유사하도록 유도
• Disparity loss : 이웃 프레임의 두 대응하는 포인트에서 렌더링된 볼륨 3D 포인트가 유사한 $z$ 값을 가지도록 강제
• Monocular depth loss : 볼륨 렌더링 깊이와 사전 계산된 MiDaS 깊이 사이의 스케일 및 shift-invariant loss를 계산

정적 영역에서 예측 $\hat\mathbf C^s(\mathbf r)$와 캡처된 이미지 사이의 photometric loss을 최소화한다:

• M : motion mask

복잡한 카메라 궤적을 처리하기 위해 추가로 auxiliary loss를 도입하여 훈련을 정규화한다.

1. Reprojection loss $L^s_\text{reproj}$ : RAFT에 의해 추정된 2D optical flow를 사용하여 훈련한다. 먼저, 표면 점을 생성하기 위해 모든 샘플링된 3D 점을 ray를 따라 볼륨 렌더링한다. 그런 다음 이 점을 이웃 프레임에 재투영하고 RAFT에서 추정된 대응값으로 reprojection error를 계산한다.

   RAFT: Recurrent All-Pairs Field Transforms for Optical Flow
   optical flow estimation model인 RAFT는 픽셀당 feature를 추출하고 픽셀의 모든 쌍에 대해 multi-scale 4D correlation volume을 구축한다. 이후 이 correlation volume에 대해 검색하는 recurrent unit을 통해 flow field를 업데이트 한다.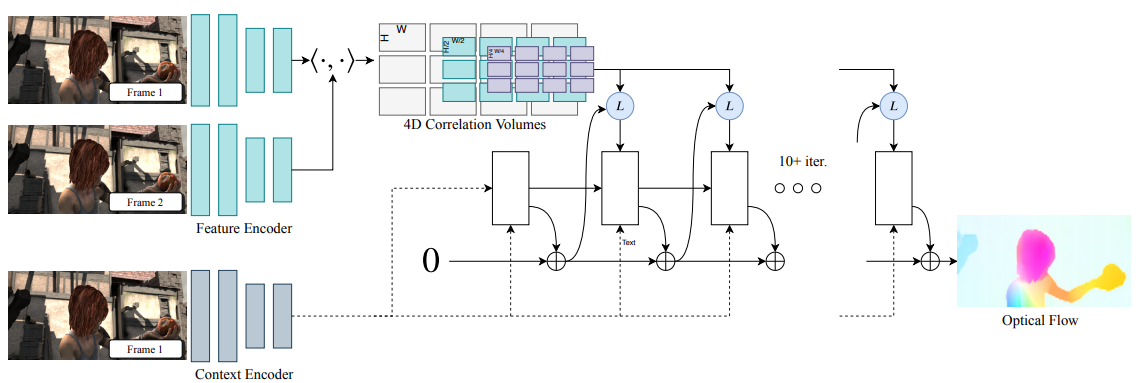

   

2. Disparity loss L $L^s_\text{disp}$: reprojection loss과 유사하게 $z$-방향(카메라 좌표)의 error를 정규화한다. 볼륨을 통해 두 개의 해당 점을 3D 공간으로 렌더링하고 $z$ component의 error를 계산한다. 먼 것보다 가까운 것에 더 집중하기 때문에 inverse-depth domain에서 이 loss를 계산한다.

3. Monocular depth loss실 $L^s_\text{monodepth}$: 위 두 loss는 순수 회전 카메라를 처리할 수 없으며 종종 잘못된 camera pose와 geometry로 이어진다(그림 4(b)). monocular depth map의 순서와 일치하도록 동일한 프레임의 여러 픽셀에서 깊이 순서를 강제한다. MiDaSv2.1 을 사용하여 depth map을 사전 계산한다. MiDaS의 깊이 예측은 알 수 없는 스케일과 이동까지이다. 따라서 렌더링된 깊이 값을 제한하기 위해 MiDaS에서 동일한 scale- 및 shift-invariant loss를 사용한다.

   MiDaS
   MiDaS는 단일 이미지로부터 상대적 역 깊이(relative inverse depth)를 계산하는 모델이다.

Optical flow와 depth map이 정확하지 않을 수 있기 때문에, 훈련 중에 이러한 auxiliary loss의 가중치에 대해 annealing을 적용한다. 입력 프레임이 동적 물체를 포함하므로, 이 모든 loss와 L2 reconstruction loss를 적용하면서 모든 동적 영역을 마스킹해야 한다.

Annealing
최적화 알고리즘 중 하나로, 함수의 최솟값을 찾는 과정에서 파라미터 값을 조정하는 방법이다. 이 방법은 주로 복잡한 최적화 문제에서 사용되며, 전역 최솟값에 빠르게 수렴하기 위해 파라미터 값을 조정하는 과정을 포함한다.

정적 부분에 대한 최종 loss :

3.4. Dynamic Radiance Field Reconstruction

Handling temporal information

Voxel에서 time-varying feature를 쿼리하기 위해 먼저 3D 좌표 $(x, y, z)$를 time index $t_i$와 함께 coordinate deformation MLP로 전달한다. coordinate deformation MLP는 3D time-varying deformation vector $( ∆x, ∆y, ∆z)$를 예측한다. 이후 이러한 변형을 원래 좌표에 추가하여 deformed coordinate $(x ′, y′, z′)$를 얻는다. 이 deformation MLP는 voxel이 canonical space이고 서로 다른 시간의 각 해당 3D 지점이 이 voxel space에서 동일한 위치를 가리켜야 함을 나타낸다. original camera space 에서 canonical voxel space로 3D 지점을 변형하도록 deformation MLP를 설계한다.

그러나 시간 차원을 따라 전체 시퀀스를 나타내기 위해 단일 compact canonical voxel을 사용하는 것은 매우 어렵다. 따라서 시간에 따라 변하는 색상과 밀도를 예측하기 위해 voxel에서 쿼리된 feature를 향상시키기 위해 time-dependent MLP를 추가로 도입한다. 여기서 MLP의 목적은 canonical voxel에서 쿼리된 feature를 더욱 향상시키기 위한 것이므로, 2~3개의 레이어만 있는 time-dependent MLP는 다른 동적 뷰 합성 방법의 것보다 훨씬 더 얕다. time-varying 효과의 대부분은 여전히 coordination deformation MLP에 의해 수행된다.

동적 영역에 대한 photometric training loss는 다음과 같다:

Scene flow modeling

동적 움직임을 더 잘 모델링하기 위해 external prior에 기반한 세 가지 loss를 도입한다. 3D 움직임을 잘 포착하기 위해 scene flow MLP를 도입한다.

• $S_{i→i+1}$ : 3D scene flow of the 3D point $(x, y, z)$ at time $t_i$
• 3D scene flow을 사용하면 dynamic radiance field에 loss를 적용할 수 있다. 그림3(b)의 훈련 손실을 보인다

1. Reprojection loss $L^d_\text{reproj}$: scene flow MLP에서 포즈, 깊이 및 추정된 3D scene flow을 사용하여 2D flow를 유도한다. 그리고 이 induced flow의 error를 RAFT에 의해 추정된 것과 비교한다.
2. Disparity loss $L^d_\text{disp}$: 정적 부분의 disparity loss과 유사하지만, 여기에 3D scene flow이 추가로 있다. 3D 공간에서 해당 지점을 얻고, 추정된 3D scene flow을 추가하며, inverse-depth domain의 z 성분의 차이를 계산한다.
3. Monocular depth loss L$L^d_\text{monodepth}$: MiDaSv2.1을 사용하여 미리 계산된 깊이 맵으로 렌더링된 깊이 사이의 scale- 및 shift-invariant loss을 계산한다.

매끄럽고 작은 scene flow loss를 도입하여 MLP의 3D 움직임 예측을 더욱 정규화한다:

scene flow MLP는 렌더링 프로세스의 일부가 아니라 loss의 일부이다. 3D scene flow를 MLP로 표현하고 적절한 사전 작업을 수행함으로써 밀도 예측을 더 우수하고 합리적으로 만들 수 있다. 또한 dynamic radiance field에서 카메라 포즈로 그래디언트를 분리한다. 마지막으로 motion mask $\mathbf M$으로 비강성 마스크 $\mathbf M^d$를 감독한다:

동적 부분의 전체 loss :

예측된 nonrigidity $m^d$를 사용하여 정적 및 동적 부분을 최종 결과로 선형 구성한다:

Total training loss

3.5. Implementation Details

• camera pose, focal length, static 및 dynamic radiance field를 동시에 추정한다. forward-facing scene의 경우 정규화된 장치 좌표(NDC)로 장면을 매개 변수화한다. 야생 비디오의 unbounded scene을 처리하기 위해 contraction parameterization를 사용하여 장면을 매개 변수화한다.
• 견고한 표면 장면 재구성을 장려하고 부유물을 방지하기 위해 distortion loss을 추가한다.
• NDC와 contraction의 경우 가장 높은 voxel 해상도를 각각 262,144,000과 27,000,000으로 설정한다. 또한 모델 압축을 위해 TensoRF의 VM-decomposition을 사용하여 voxel grid를 분해한다.
• 하나의 NVIDIA V100 GPU로 전체 교육 과정은 약 28시간이 소요된다.