[Paper Review] NeRF-DS: Neural Radiance Fields for Dynamic Specular Objects

E0u0n·2023년 10월 15일

NeRF

목록 보기

5/12

Paper : NeRF-DS: Neural Radiance Fields for Dynamic Specular Objects

Abstract

배경

렌더링을 위해 observation space에서 공통 canonical space으로 프레임 전체의 이동 지점을 warping하지만, dynamic NeRF는 warping하는 동안 반사되는 색상의 변화를 모델링하지 않는다.
→ 이 접근 방식은 움직이는 반사 물체에서는 실패하는 경우가 많다.

제안

Observation space의 표면 위치와 방향에 따라 조절되도록 neural radiance field 함수를 재구성한다.
→ 다양한 pose의 specular surface가 공통 canonical space에 매핑될 때 서로 다른 반사 색상을 유지할 수 있다.

Deformation field를 학습하기 위해 움직이는 물체의 mask를 추가한다.
→ specular surface가 움직이는 동안 색상이 변하기에 mask는 RGB 감독만으로 시간적 대응을 찾지 못하는 문제를 완화한다.

결과

기존 NeRF 모델에 비해 monocular RGB 비디오에서 움직이는 반사 물체의 재구성 품질을 크게 향상시킨다.

3. Dynamic NeRF Preliminaries

NeRF는 장면의 volumetric representation $F : (\mathbf x, ωo) → (σ, c)$ 이다. MLP는 spatial position $\mathbf x$ 를 volume density $σ(\mathbf x)$ 및 bottleneck $b(\mathbf x)$ 에 매핑하는 데 사용된다. 또 다른 MLP head는 bottleneck $b(\mathbf x)$ 및 viewing direction(또는 outgoing radiance direction) $ω_o$ 를 사용하여 해당 지점의 색상 $c(\mathbf x, ω_o)$ 를 예측한다:

c(\mathbf x, ω_o)=F(\mathbf x, ω_o). \tag 1

장면의 이미지를 렌더링하기 위해, 카메라 중심 $\mathbf o$ 로부터 각 픽셀 ray $r$ 에 대해 $N$ 개의 샘플 $\mathbf x_i = \mathbf o - k_iω_o$ 을 가져온다. 픽셀 색상 $C(r)$ 는 이러한 샘플링된 지점의 색상에 대한 가중 합이다. 이때 가중치는 step size $δ_i$ 및 ray를 따르는 local volume density에 기반한 누적 투과율 $α_i$ 의 곱이다:

\alpha_i=\exp \left(-\sum_{j=1}^{i-1} \sigma_i \delta_i\right), w_i=\alpha_i\left(1-\exp \left(-\sigma_i \delta_i\right)\right) (2\text a) \\ C(r)=\sum_{i=1}^N w_i \cdot c_i \,\,\,\,\,\,\,\,\,\,(2\text b)

Dynamic NeRF는 단안 RGB 카메라 영상으로부터 3D 동적 장면을 재구성한다. 동적 장면의 객체는 시간에 따라 이동하거나 변형될 수 있으므로 장면의 각 순간에 대해 하나의 프레임만 사용할 수 있다. Multi-view 영상 없이 장면의 3D 구조를 재구성하는 것은 어렵다. 따라서 대부분의 동적 NeRF는 deformation field $T : \mathbf x → \mathbf x'$ 를 사용하여 시간 $t$ 의 observation space에서 공통 canonical space으로 장면을 변환한다. 이 공통 canonical space을 활용하여 다양한 시간과 veiw의 영상을 사용하여 정적 NeRF 모델 $F(\mathbf x', ω_o)$ 로 장면을 재구성할 수 있다:

c(\mathbf x, ω_o, t)=F(T(\mathbf x, t),ω_o)=F(\mathbf x',ω_o). \tag 3

실제로, 샘플링된 observation space 좌표 $\mathbf x$ 와 time embedding $ϕ_t$ 는 deformation field prediction MLP에 입력되어 canonical space 좌표 $\mathbf x'$ 를 예측한다. HyperNeRF는 다른 MLP를 사용하여 $\mathbf x$ 와 $ϕ_t$ 로부터 hyper canonical 좌표 $\mathbf w$ 를 예측한다. Canonical 좌표 $\mathbf x'$ 와 $\mathbf w$ 는 볼륨 밀도 $σ$ 을 예측하기 위해 canonical NeRF MLP에 제공된다. Canonical NeRF MLP의 색상 예측 head는 viewing direction $ω_o$ 를 받아들여 색상 c를 출력한다. 기존의 동적 NeRF $F(\mathbf x', ω_o)$ 는 동적 반사 물체를 렌더링할 때 under-parameterizing된다. 특히, 색상은 observation space 표면 법선 $\mathbf n$ 과 위치 $\mathbf x$ 에도 의존해야 한다. 따라서 본 논문은 모델을 $F(\mathbf x', ω_o,\mathbf x, \mathbf n)$ 로 확장할 것을 제안한다.

4. Our Method: NeRF-DS

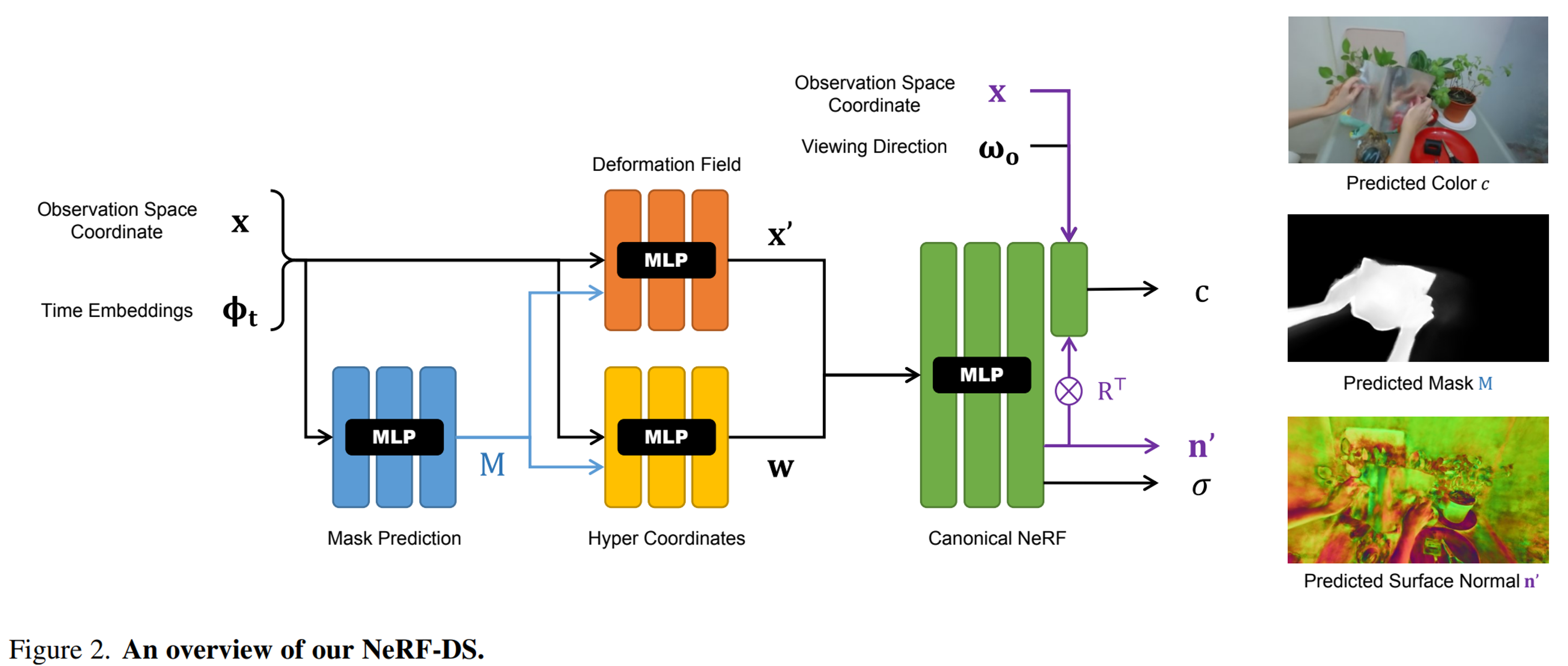
Observation space 좌표 $\mathbf x$ 및 time embedding $\phi_t$ 로부터 움직이는 물체의 3D mask $\text M$ 를 예측한다. Mask는 $\mathbf x$ 및 $\phi_t$ 와 함께 deformation field 및 hyper-coordinate(파란색 화살표)을 예측하는 데 사용된다.
Canonical NeRF 모델은 canonical space 좌표 $\mathbf x'$ 와 hyper-coordinate $\mathbf w$ 를 사용하여 부피 밀도 $σ$ 및 canonical 표면 법선 $\mathbf n'$ 을 예측한다. 회전된 표면 법선 $\mathbf n$ 과 observation space의 좌표 $\mathbf x$ 는 viewing direction $ω_o$ 와 함께 color branch(보라색 화살표)에 공급되어 색상을 예측한다.
색상과 mask는 볼륨 렌더링 후 2D ground truth를 사용하여 감독되고, 표면 법선은 부피 밀도의 negative gradient로 감독된다.

4.1 절

NeRF-DS는 observation space에서 정확한 반사 색상을 예측하기 위해 추가적인 observation space 좌표 $\mathbf x$ 와 orientation $\mathbf n$ 에 대해 조정된 canonical NeRF를 포함한다.
$\mathbf x$ 는 ray 샘플에서 얻어지며 annealing된 positional encoding이 추가된다. $\mathbf n$ 은 canonical space에서 예측된 표면 법선 $\mathbf n'$ 을 warping하여 얻는다.

4.2 절

specular 표면의 대응 및 deformation field를 더 잘 학습하기 위해, deformation field과 hyper coordinate 예측은 움직이는 물체의 mask $M$ 을 사용한다.
$M$ 은 mask prediction MLP에 의해 예측되고 2D ground truth에 의해 감독된다.

4.1. Surface-Aware Dynamic NeRF

컴퓨터 그래픽스에서 specular surface의 렌더링은 일반적으로 렌더링 방정식에 기초한다(Rendering equation):

L_o(\mathbf x, ω_o)=L_e(\mathbf x, ω_o)+L_r(\mathbf x, ω_o)\tag 4

$\mathbf x, ω_{\mathbf i}, ω_o, \mathbf n$ : spatial coordinates, incident angle, outgoing angle, surface normal
$L_o(\mathbf x, ω_o)$ : Outgoing radiance
$L_e(\mathbf x, ω_o)$ : 대상 물체가 광원일 때 emission light
$L_r(\mathbf x, ω_o)=\int_\Omega \rho(\mathbf x, ω_{\mathbf i}, ω_o)L_i(\mathbf x, ω_{\mathbf i})(ω_{\mathbf i}\cdot \mathbf n)d\omega$ : BRDF $\rho$ 및 환경 맵 $L_i$ 을 기반으로 상반구 $\Omega$ 에 걸쳐 들어오는 모든 radiance $ω_i$ 의 나가는 reflected radiance를 적분하는 반사 성분

BRDF(Bidirectional reflectance distribution function)
특정 입사각과 반사각에 대해서 빛이 반사되는 정도에 대한 분포를 나타내는 함수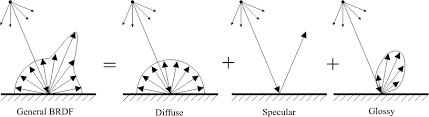

https://cw.fel.cvut.cz/b201/_media/courses/b4m39rso/lectures/03-x39rso-brdf.pdf

NeRF 모델에서 radiance 색상 $L_o(\mathbf x, ω_o)$ 은 모든 reflected radiance를 explicit하게 적분하는 대신, implicit하게 표현한다. 이후 반사 성분을 함수 $L_r(\mathbf x, ω_o, \mathbf n)$ 로 단순화할 수 있다:

L_o(\mathbf x, ω_o)=L_e(\mathbf x, ω_o)+L_r(\mathbf x, ω_o,\mathbf n). \tag 5

자기 반사가 없다고 가정하면 반사되는 색은 모두 광원 또는 정적인 환경의 물체에서 나온 것이며, 식 (5)의 공간 좌표 $\mathbf x$ , viewing direction $ω_o$ 및 표면 법선 $\mathbf n$ 은 observation space 내에서 표현된다.

정적 장면에서는 객체의 표면이 움직이지 않으므로 observation space과 canonical space 사이에 차이가 없다. 결과적으로 표면 법선 $\mathbf n$ 은 $N(\mathbf x)$ 로 표시되는 $\mathbf x$ 의 함수로 간단히 나타낼 수 있다:

L_o(\mathbf x, ω_o)=L_e(\mathbf x, ω_o)+L_r(\mathbf x, ω_o,\mathbf N(\mathbf x))=F(\mathbf x, ω_o). \tag 6

동적 NeRF에서, 움직이는 물체는 먼저 observation space으로부터 공통의 canonical space으로 매핑되어 렌더링된다. 동일한 canonical space 위치 $\mathbf x'$ 와 viewing direction $ω_o$ 에 있는 점들은 NeRF MLP $F(\mathbf x, ω_o)$ 를 사용하여 동일한 색으로 렌더링된다. 그러나 식 (5)의 렌더링 방정식에서 설명된 바와 같이, specular surface의 색은 observation space 위치 $\mathbf x$ 와 표면 법선 $\mathbf n$ 에 의존한다. 동일한 $\mathbf x'$ 와 $ω_o$ 지만 다른 $\mathbf x$ 와 $\mathbf n$ 을 갖는 점들은 다른 색을 반사할 수 있다.

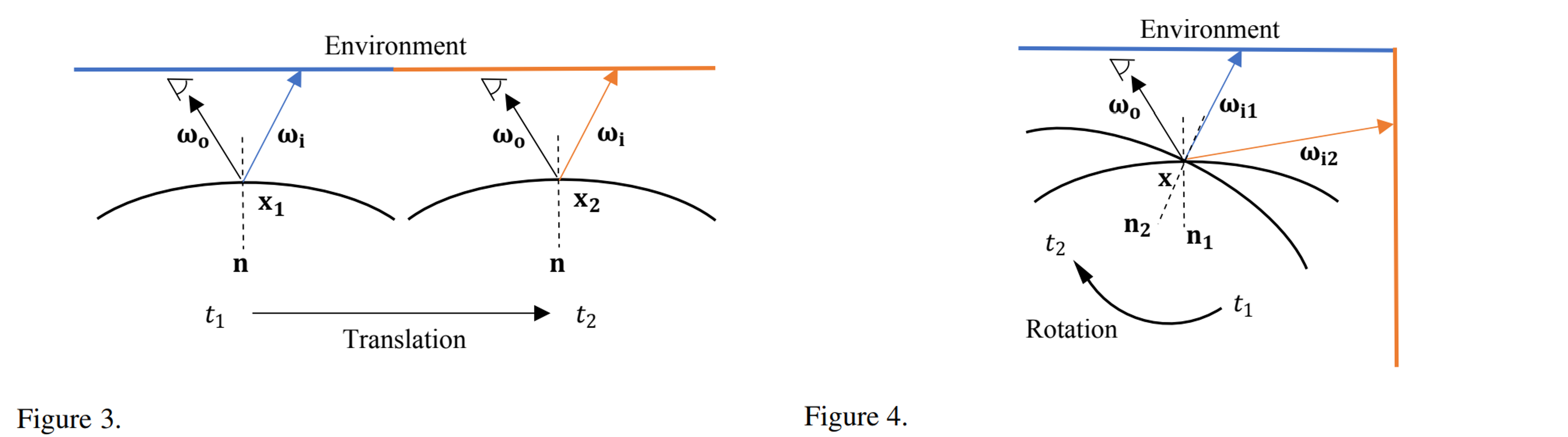
$F : (\mathbf x', ω_o) → (σ, c)$ 형태의 기존의 동적 NeRF는 이 경우 under-parameterization 함수가 된다.

그림 3에서 기존의 동적 NeRF는 translation한 점 $\mathbf x_1$ 과 $\mathbf x_2$ 를 canonical space의 동일한 점, 즉 $T(\mathbf x_1, t_1) = T(\mathbf x_2, t_2) =\mathbf x'$ 으로 왜곡한다. NeRF 모델 $F(\mathbf x', ω_o)$ 는 다른 색을 반사하는 대신 동일한 색으로 잘못 렌더링한다.
그림 4에서 기존의 동적 NeRF는 표면 법선 방향을 무시한다. NeRF 모델 $F(\mathbf x', ω_o)$ 는 회전 전후 점 $\mathbf x$ 를 다른 색으로 반사하는 대신에 동일한 색으로 잘못 렌더링한다.

본 연구는 동적 NeRF에서 under-parameterization 문제를 해결하기 위해 식 (5)에 이어 surface-aware dynamic NeRF를 도입한다. Observation space의 표면 정보는 specular surface 색상을 렌더링하기 위해 canonical NeRF 모델에 제공된다. 구체적으로, 부피 밀도 예측 분기를 변경하지 않은 채로 NeRF 색상 예측 분기(그림 2의 보라색)의 입력에 observation space 좌표 $\mathbf x$ 와 표면 법선 $\mathbf n$ 을 추가한다. 그러면 수정된 NeRF 함수는 다음과 같이 표현될 수 있다:

L_o(\mathbf x, ω_o)=L_e(\mathbf x, ω_o)+L_r(\mathbf x, ω_o,\mathbf N(\mathbf x))=F(\mathbf x, ω_o,\mathbf x,\mathbf n). (7 \text a)\\ F:(\mathbf x', ω_o,\mathbf x,\mathbf n)→(\sigma(\mathbf x'),c(\mathbf x',ω_o,\mathbf x,\mathbf n)).(7 \text b)

모델이 observation space에서 직접 렌더링되어 공유 canonical space를 무시하는 것을 방지하기 위해 Nerfies와 같이 annealing된 position encoding $\gamma_\tau(\mathbf{x})$ 을 사용하여 observation space 좌표 $\mathbf{x}$ 를 입력한다:

z_j(\tau)=\frac{1-\cos (\pi \cdot \operatorname{clamp}(\tau-j, 0,1))}{2} (8 \text a)\\ \gamma_\tau(\mathbf{x})=\left(\cdots, z_k(\tau) \sin \left(2^k \pi \mathbf{x}\right), z_k(\tau) \cos \left(2^k \pi \mathbf{x}\right), \cdots\right.). (8 \text b)

$τ$ 의 값은 0으로 초기화되고 훈련 중에 천천히 증가하여 초기 훈련 단계에서 $\mathbf{x}$ 를 모델에서 완전히 잘라냄

그러나 표면 법선 $\mathbf{n}$ 은 NeRF와 같은 volumetric 모델에서 직접 추출할 수 없다. 이를 해결하기 위해 먼저 canonical space 좌표 $\mathbf{x}$ 에 대한 부피 밀도 $σ$ 의 negative gradient를 가진 canonical space 표면 법선 $\bar\mathbf n'$ 을 추정한다:

\bar\mathbf n'=-\frac{\nabla\sigma(\mathbf x')}{\|\nabla\sigma(\mathbf x')\|} \tag 9

그러나 부피 밀도 $σ$ 의 1차 미분은 직접적인 감독 없이는 noise가 많다. 따라서 추정된 $\bar\mathbf n'$ 을 사용하여 NeRF MLP로부터 더 매끄럽게 예측된 표면 법선 $\mathbf n'$ 을 감독하고 Ref-NeRF와 같이 역방향 법선에 페널티를 적용한다.

\begin{gathered} \mathcal{L}_{\text {norm }}=\sum_i w_i\left\|\mathbf{n}^{\prime}-\overline{\mathbf{n}}^{\prime}\right\|^2 \\ \mathcal{L}_{\text {backward }}=\sum_i w_i \cdot \max \left(0, \mathbf{n}^{\prime} \cdot-\omega_o\right) \end{gathered} \tag {10}

observation space에서 canonical space으로의 deformation field로 3D special Euclidean group $(\text{SE(3)) T}(x) = [\text R | \mathbf t]\mathbf x$ 를 사용한다. 마지막으로, 다음을 사용하여 canonical space 표면 $\mathbf n'$ 을 observation space 표면 $\mathbf n$ 으로 되돌릴 수 있다:

\mathbf{n}=\text R^\top\mathbf{n}'. \tag {11}

Canonical space에서 표면 법선을 예측한 후 warping함으로써 시간 경과에 따른 표면 법선 일관성이 보장된다. 시간 $t_1$ 과 $t_2$ 에서 두 대응점의 표면 법선 $\mathbf n_1$ 과 $\mathbf n_2$ 는 $\mathbf n_1 = \text R^⊤_1 \text R_2\mathbf n_1$ 과 관련된다. Observation space의 표면 법선은 예측된 canonical 표면 법선에서 warping되어 있다. RGB 값은 정규화된 surface norm vector의 xyz 성분을 나타낸다.

4.2. Mask Guided Deformation Field

대부분의 non-specular 물체는 움직일 때 색이 급격하게 변하지 않는다. 그러나 식 (5)와 같이 specular 물체의 색은 다른 위치와 방향에서 크게 변할 수 있다. 동적 NeRF의 변형은 RGB 감독으로부터만 학습된다. 동일한 점의 색이 너무 많이 변하면 점 대응이 거의 성립되지 않는다. 결과적으로 모델은 그림 6과 같이 deformation field을 완전히 학습하지 못하는 경우가 많다.

이 문제를 해결하기 위해 이동 물체의 2D mask를 사용한 mask guided deformation field을 도입한다. specular surface의 색이 급격하게 변하는 것과 달리 이 mask는 물체가 움직이는 동안 일관성을 유지한다.
(mask는 specular surface에 대한 deformation field 예측을 위한 의미 있는 guidance를 제공하며, deformation fiel에 대한 deformation prediction network에 강력한 단서를 제공한다.)

따라서 observation space의 각 3D 지점에서 mask 값을 예측하는 mask prediction network $G : \mathbf x → \text M$ 을 추가한다. 예측된 mask $\text M$ 은 deformation field 및 hyper-coordinate prediction network(그림 2의 파란색)에 입력된다. 예측된 3D mask는 볼륨 렌더링을 사용한 훈련 view에서 2D mask $\bar\text M$ 에 의해 감독된다:

\mathcal L_{mask}=\|(\sum^N_{i=1}w_i\cdot\text M)-\bar\text M\|^2. \tag {12}

2D mask는 이진값이므로 mask 예측은 색상 예측보다 모호하다. $w_i$ 대신 더 날카로운 가중치 $w'_i$ 를 사용하여 3D mask가 물체 표면 근처에서 예측되도록 권장한다. 이는 각 샘플 $\mathbf x_i = \mathbf o + k_iω_o$ 에 대한 가중치 $w_i$ 에 Gaussian multiplier를 적용하여 계산된다. Gaussian $\mathcal N$ 은 최대 가중치 위치 $k_\text{max}$ 의 중심에 있으며 훈련 중 표준 편차 $β$ 가 감소한다:

w_i^*=w_i \cdot P\left(k_i \mid \mathcal{N}\left(k_{\max }, \beta\right)\right), w_i^{\prime}=w_i^* /\left(\sum_j w_j^*\right) \tag {13}

그림 6과 같이, mask guided deformation field는 더 의미 있는 deformation field를 예측한다.

이 mask가 camera pose registration 동안 대부분의 동적 NeRF에 이미 필요하다는 것에 주목한다. 올바른 등록을 위해 움직이는 전경 특징을 모션 구조 알고리즘에서 마스킹해야 하므로 파이프라인에 추가 입력을 도입하지 않는다. 이 마스크 없이 추정된 포즈는 특히 움직이는 부분이 이미지에서 클 때 훨씬 더 낮은 정확도를 가질 수 있다. 예를 들어, 마스크가 없는 "basin" 장면에서 추정된 카메라 포즈는 Procrustes 정렬 후 원래 포즈에서 31.7% 벗어났다. 이러한 포즈에 대해 훈련된 HyperNRF는 PSNR에서 6.9%, LPIPS에서 82.7% 성능이 떨어진다.