Abstract

문제

• 기존 grid-based NeRF 프레임워크는 주로 bounded scene을 위해 설계되었으며 unbounded scene을 처리하기 위해 space warping에 의존
• 기존 space warping 방법은 forward-facing 궤적 또는 360° object-centric 궤적만을 위해 설계되었을 뿐 임의의 궤적 처리 불가

제안

• grid-based NeRF 프레임워크에서 임의의 궤적을 처리할 수 있는 perspective warping이라는 새로운 space warping 방법 제안
• 임의의 입력 카메라 궤적을 가능하는 grid-based NeRF의 일종 F$^2$-NeRF (Fast-Free-NeRF) 제시

결과

• 제안 wariping 방법이 두 표준 데이터 세트와 수집한 자유 궤적 데이터 세트에서 고품질 이미지 렌더링 가능함을 입증

1. Introduction

NeRF의 등장으로 novel view synthesis의 연구가 급격하게 발전했다. NeRF의 핵심 아이디어는 1) 3D scene을 MLP network를 통해 인코딩하여 density field와 radiance field로 표현하는 것과, 2) 미분 가능한 volume rendering 기술로 MLP network를 최적화하는 것이다. NeRF는 photo-realistic 렌더링 결과를 달성했지만, 매우 긴 training time으로 적용 범위가 제한된다.

최근 연구인 Plenoxels, DVGO, TensoRF 및 Instant-NGP와 같은 grid-based 방법은 몇 분 이내에 NeRF를 빠르게 훈련 가능함을 보인다. 그러나 이러한 방법은 scene의 크기에 따라 cubic 순서로 메모리 소비가 증가한다. 이를 줄이기 위해 voxel pruning, tensor decomposition, hash indexing과 같은 다양한 기술이 제안되었지만, 여전히 original Euclidean space에 그리드가 구축될 때 bounded scene만 처리할 수 있다.

Space warping

unbounded scene을 표현하기 위해 일반적인 전략은 unbounded scene을 bounded space에 매핑하는 space-warping 방법을 사용하는 것이다. warping function은 일반적으로 두 가지 종류가 있다.

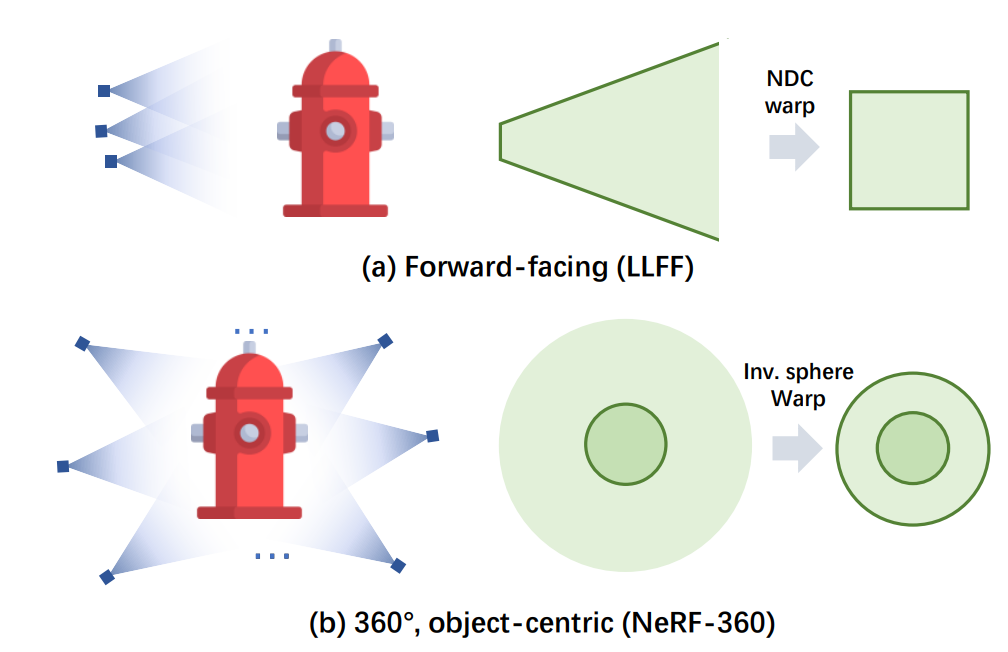
1. For forward-facing scene (a)
   Normalized Device Coordinate(NDC) warping으로 z 축을 따른 공간을 왜곡하여 무한히 먼 view frustum을 bounded box에 매핑
2. 360° object-centric unbounded scene (b)
   inverse-sphere warping으로 sphere inversion transformation을 통해 무한히 큰 공간을 경계가 있는 구에 매핑

이 두 warping 방법은 특수 카메라 궤적 패턴이나 임의의 카메라를 처리할 수 없다. 특히 궤적이 길고 여러 관심 대상을 포함하는 free trajectory의 경우 렌더링된 이미지의 품질이 저하된다.

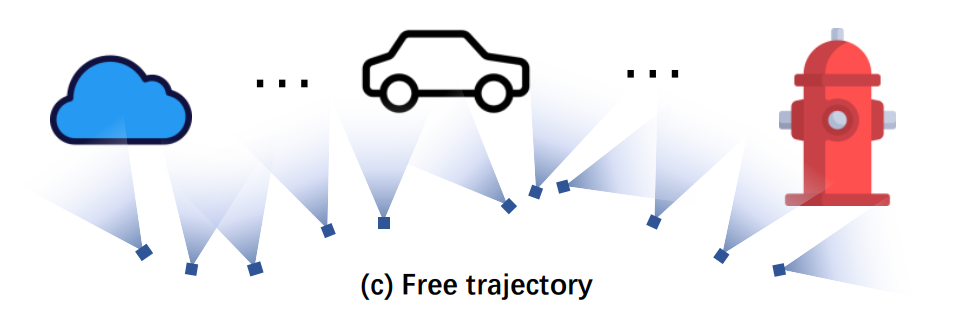
Free trajectory에 대한 성능 저하는 공간 표현 용량의 불균형한 할당으로 인해 발생한다. 특히 궤적이 좁고 긴 scene은 많은 영역이 비어 있고 input view에도 보이지 않는다. 이러한 빈 공간의 낭비는 voxel pruning, tensor decomposition, hash indexing을 사용하여 완화될 수 있지만 제한된 GPU 메모리로 인해 여전히 흐린 이미지를 유발한다.

위 문제를 해결하기 위해 F$^2$-NeRF는 임의의 카메라 궤적에 적용할 수 있는 perspective warping이라고 하는 space-warping 체계를 제안한다.

1. input image에서 $\mathbf p$의 투영의 2D 좌표를 연결하여 3D 점 $\mathbf p$의 위치를 나타낸다.
2. PCA를 사용하여 이러한 2D 좌표를 소형 3D 하위 공간으로 매핑한다.

또한 이 방법을 grid-based NeRF 프레임워크에서 구현하기 위해 배경에는 coarse grid를, 전경에는 fine grid를 적응적으로 사용하는 space subdivision 알고리즘을 추가로 제안한다.

F$^2$-NeRF (Fast-Free-NeRF)는 Instant-NGP의 프레임워크를 기반으로 구축되어 다양한 카메라 궤적을 가진 unbounded scene에서 효율적으로 training되며, hash-grid representation의 빠른 수렴 속도를 유지한다.

Experiments

Dataset : unbounded forward-facing dataset, unbounded 360° object-centric dataset, new unbounded free trajectory dataset
Free camera trajectory free Dataset에서는 baseline grid-based NeRF 방법을 능가하며 2080Ti GPU에서 training하는 데 12분이 걸린다.

3. Approach

3.1. Overview

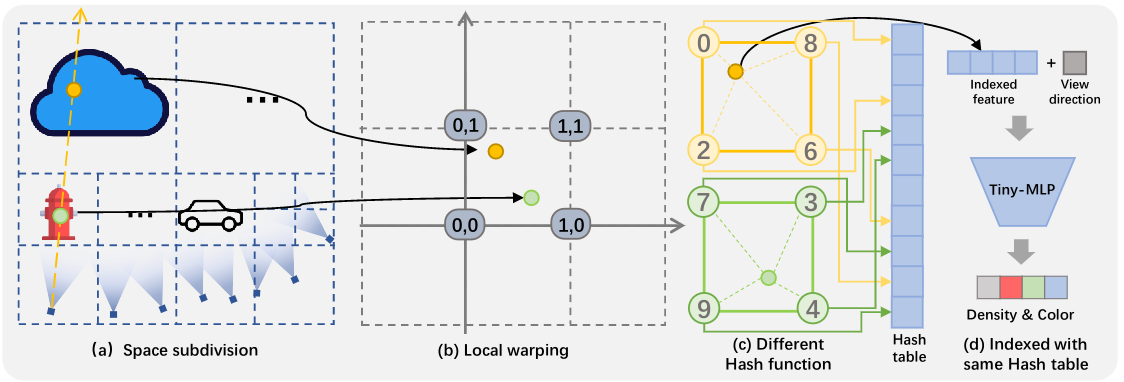
렌더링 절차를 준비 단계와 실제 렌더링 단계로 요약한다.

1. 준비 단계에서는 카메라의 view frustum에 따라 Space subdivision(3.3절) 후, 각 하위 영역에 대해 선택된 카메라를 기반으로 local warping function을 구성(3.2절)
2. 렌더링 단계에서는 카메라 ray 위의 포인트를 샘플링(3.5절)하고, 샘플링된 포인트의 density와 color는 multiresolution hash grid에서 가져와서(3.4절), 가중 누적을 수행하여 렌더링

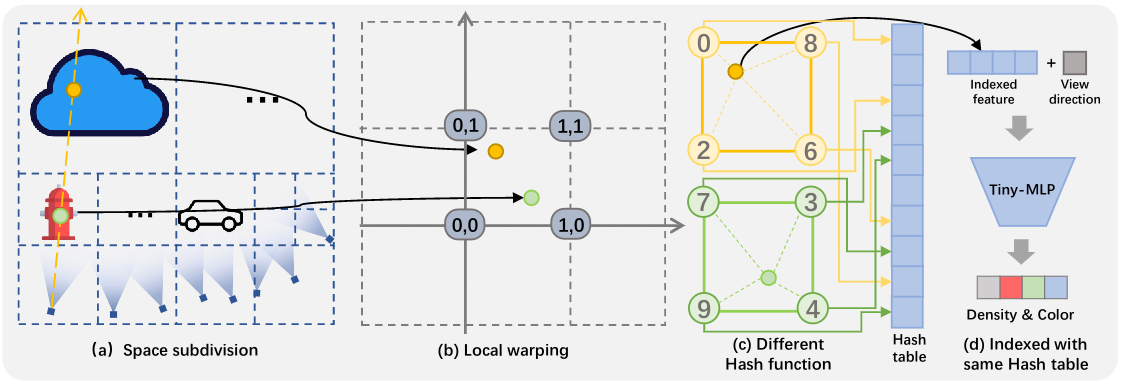
Detail

(a) 관심 영역이 큰 경우 input view frustum에 따라 공간을 세분화한다.
(b) 두 개의 다른 leaf node에 있는 녹색 점과 노란색 점이 동일한 warp space에 두 개의 다른 perspective warping function에 의해 매핑한다.
(c) 두 점이 warp space의 동일한 voxel에 있을 때, 인접한 vertex의 좌표는 동일하지만 두 점은 서로 다른 hash function을 사용하여 인접 vertex에 대해 서로 다른 hash 값을 계산한다.
(d) 이때 밀도와 색상은 동일한 해시 테이블에서 가져온다. 계산된 hash 값은 feature vector를 검색하기 위해 동일한 hash table을 indexing하는 데 사용된다.

Volume rendering with perspective warping

픽셀에 대한 색상 $\hat c$ 렌더링 과정

1. 픽셀에서 방출되는 카메라 ray의 sample point $\mathbf x_i$에 새로운 point sampling 전략 perspective sampling 적용
2. 이 sample point는 perspective warping에 의해 warp space으로 warping되며, warp space에 구축된 neural representation으로부터 sample point의 밀도 $σ_i$ 및 색상 $c_i$ 계산
3. 픽셀 색상 $\hat c$ 를 계산하기 위해 색상을 합성
   ${\hat c} =\sum_{i}T_i\alpha_ic_i \tag 1$
   • $T_i=\prod_{j=0}^{i-1}\left(1-\alpha_j\right)$ : accumulated transmittance
   • $\alpha_i=1-\text{exp}(-\delta_i\sigma_i)$ : opacity of the point

3.2. Perspective warping

Unbounded scene을 표현하기 위해 기존 NeRF에서는 NDC warping을, NeRF++, Mip-nerf 360에서는 inverse sphere warping과 같은 space warping 방법을 사용했다. 다만 이는 forward-front scene에 유용한 방법으로 임의의 궤적을 가진 scene에서는 낮은 성능을 보인다. 이에 본 논문에서는 free-trajectory scene을 렌더링하기 위해 perspective warping을 사용한다.

2D analysis

2차원 공간에서 2대의 카메라가 바라본 두 점을 1D image plane에 투영하는 상황을 가정하고 문제를 정의한다.

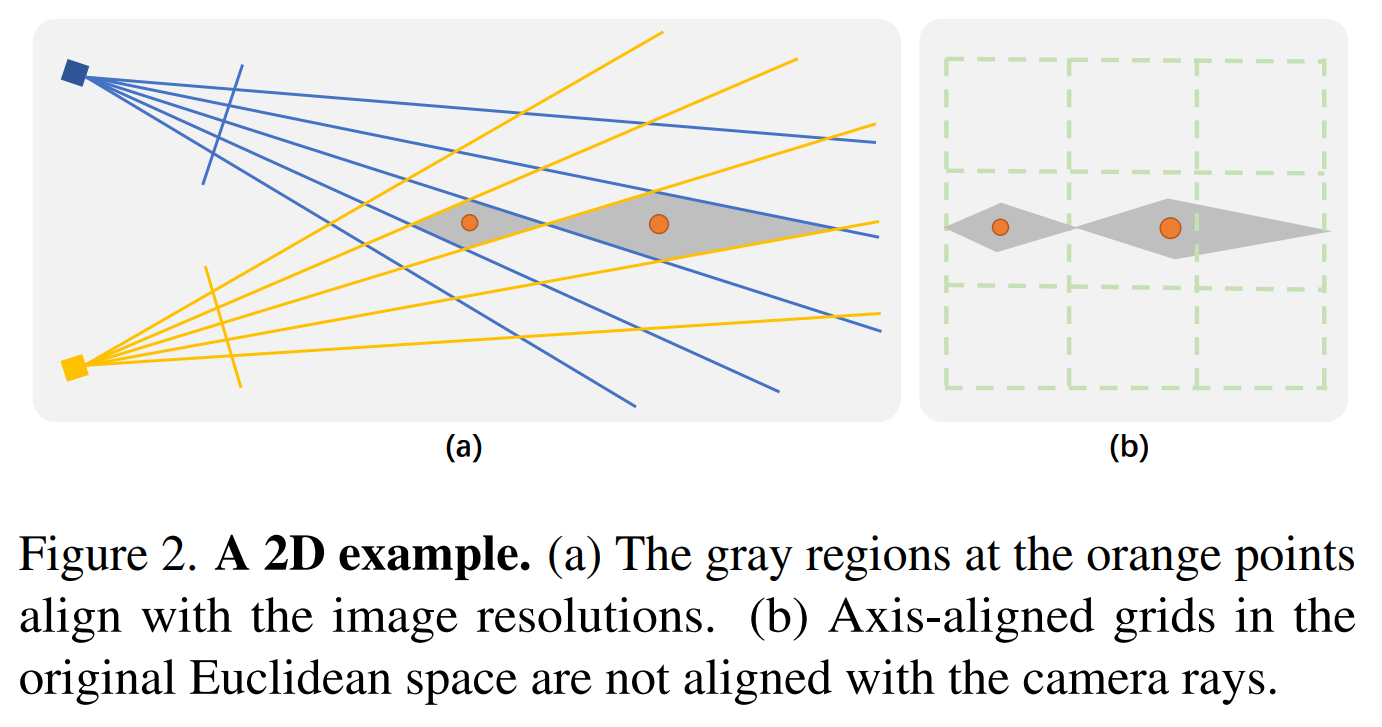
(a) 2차원 공간에서 2대의 카메라로 주황색 점을 관측 할 때, 2D 공간의 점이 1D image plane에 투영된다. 주황색 점이 있는 회색 영역은 이미지의 한 픽셀을 의미한다.
(b) 같은 scene을 original Euclidean space axis-aligned grid로 표현하였을 때, 카메라 ray와 정렬되지(일치하지) 않는다. 즉, 카메라를 통해 본 회색 범위가 axis-aligned grid에서는 서로 다른 영역에 속할 수 있다.

기존 grid-based representation은 축에 정렬된 규칙적인 그리드로 구성되어 카메라 ray로부터 구성된 회색 마름모와 일치하지 않는다. 이는 카메라로부터의 거리가 멀어질수록 더욱 심해진다. 카메라 ray가 그리드와 일치하도록 original Euclidean space를 axis-aligned grid가 구축된 공간으로 적절히 warping 해야한다.

이를 달성하기 위해 본 연구에서는 아래 definition을 만족하는 warping function을 $F(\mathbf x)=(C_1(\mathbf x),C_2(\mathbf x))$로 정의한다. 이때 $C_i(\mathbf x)$는 카메라의 image plen에 투영된 점을 의미한다.

Definition 1

• 3D Euclidean space 영역 $S$에 visible camera 세트 $\{C_i|i=1,2,...,n_c\}$ 존재
• $\mathbf x1, \mathbf x2 \in S$이라면, warping space에서의 이 두 점 사이의 거리는 모든 visible camera 공간 상에서의 두 점 간의 거리의 합과 동일

$\left\|F\left(\mathbf{x}_1\right)-F\left(\mathbf{x}_2\right)\right\|_2^2=\sum_i^n \| C_i\left(\mathbf{x}_1\right)-C_i\left(\mathbf{x}_2\right)\|_2^2$

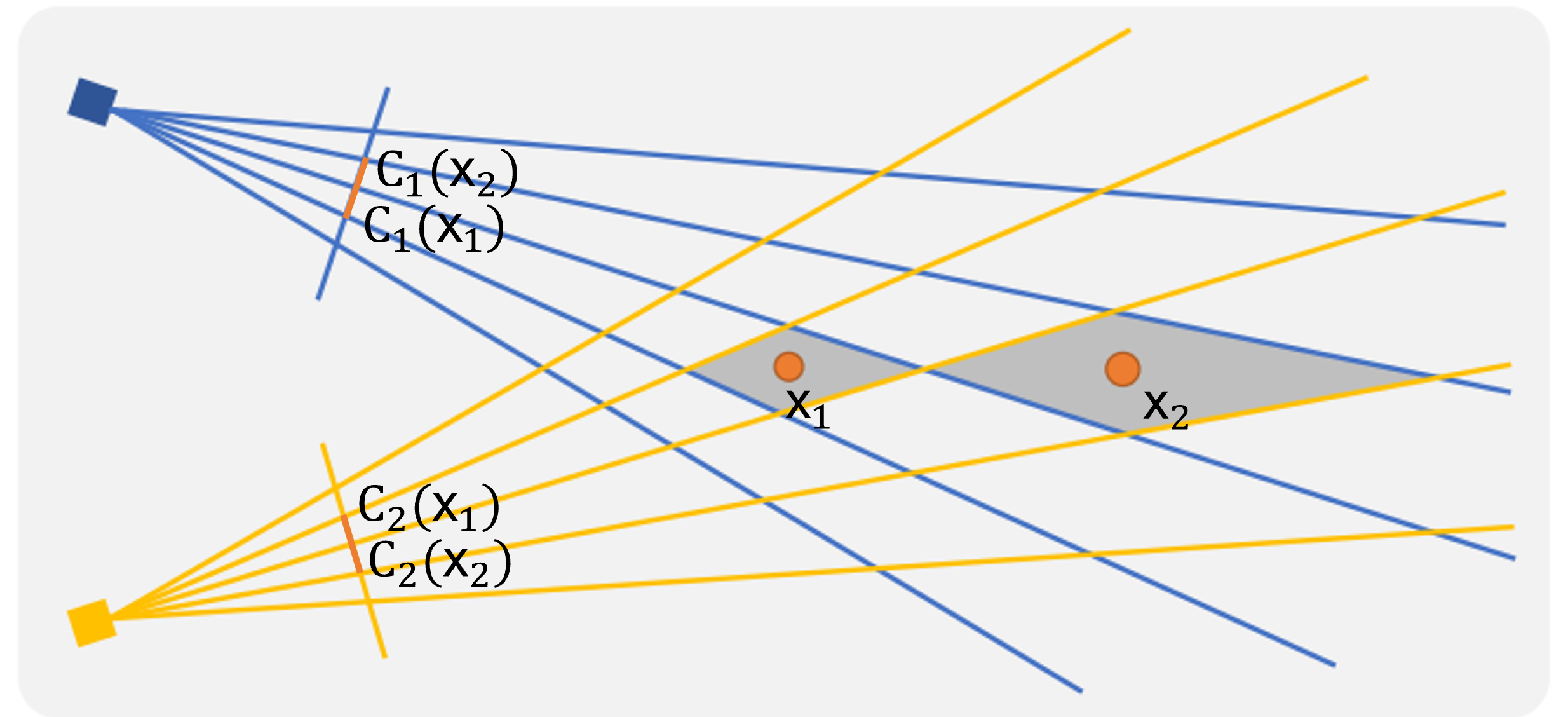
그림 2를 기반으로 2D toy eample을 설명하자면, 각 점은 warping function에 의해 $F(\mathbf x_1)=(C_1(\mathbf x_1),C_2(\mathbf x_1))=(2,1)$ 와 $F(\mathbf x_2)=(C_1(\mathbf x_2),C_2(\mathbf x_2))=(1,2)$ 로 warping된다. 위 difinition에 의거하여 계산하면 두 space에서의 두 점의 거리가 같은 것을 확인할 수 있다.

3D perspective warping

3차원에서의 warping을 고려한다면 warping function $F(\mathbf x)$는 $\mathbb R^3→\mathbb R^3$ 을 달성해야한다. 다만 이는 위 2D의 예시처럼 투영만으로써는 warping을 달성하기는 쉽지 않다.

2D 예시처럼 먼저 3D로부터 2D로의 투영을 고려해볼 수 있다. 3D point $\mathbf x$가 각 카메라 $C_1$과 $C_2$의 2D image plane에 투영된 점을 $C_1(\mathbf x)$와 $C_2(\mathbf x)$로 표현한다. 이 투영된 점들을 $G(\mathbf x)$로 정의한다.

이는 3D로부터 2D로의 올바른 warping function이지만 최종적으로 구축하고자 하는 것은 3D 공간을 다른 3D 공간으로 매핑하는 함수이다. 따라서 $G(\mathbf x)$를 이용하여 대략적으로 올바른 warping function $F(\mathbf x)$를 구축하는 것을 목표한다.

perspective warping

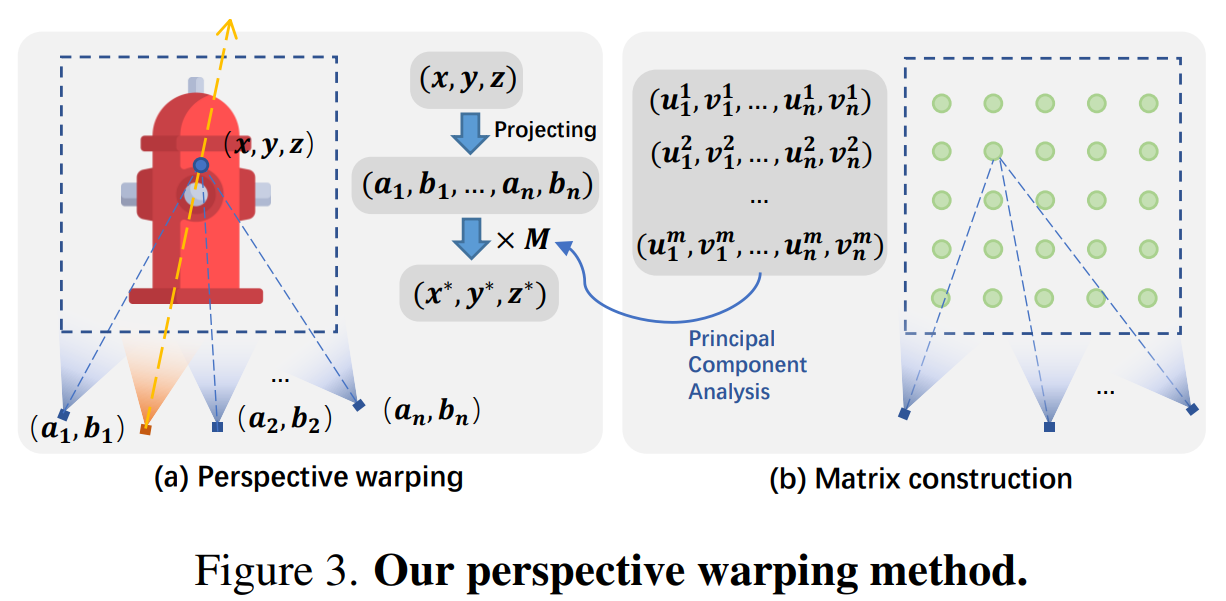
Perspective warping은 image plane으로 투영된 point $G(\mathbf x)$들을 original euclidean space에서 axis-aligned grid space로 매핑하는 함수를 통해 달성된다.

해당 perspective warping 함수는 아래와 같은 문제를 정의함으로써 시작한다.

Problem 1
Original Euclidean space의 local region $S$에서 균등하게 샘플링된 점을 $\{\mathbf x_j|j=1,2,...,n_p\}$ 라고 할 때, 죄표 $\mathbf y_j = G(\mathbf x_j) ∈ \mathbb R^{2n_c}$ 를 $\mathbf z_j = M \mathbf y_j$를 통해 $\mathbf z_j ∈ \mathbb R^3$ 에 매핑한다. 이 때, $\sum_{j}^{K}\|M^\intercal \mathbf z_j-\mathbf y_j\|_2^2$ 를 최소화하는 projection matrix(?) $M ∈ \mathbb R^{3\times2n_c}$ 을 찾고자 한다.(왜 $M^{-1}$이 아니고 $M^\intercal$인지?)

이때, 3D 영역 $S$는 space subdivision을 통해 충분히 작은 영역으로 세분화된 voxel node이며, 해당 node에 속한 visible camera를 $C_i$라고 한다.

Perspective warping을 달성하기 위해 최적화하려는 행렬 $M$은 $G(\mathbf x)$의 좌표값들의 PCA를 통해 구성된다.

Principal component analysis

최적화할 $M$을 구하기 위해서 먼저 초기 $M'$을 정의한다. 선택된 카메라의 영역 $S$가 주어지면 먼저 $S$ 내부의 $n = 32^3$개의 점 $\{\mathbf x_i\}$를 균일하게 샘플링한다. 이 샘플링한 점을 선택된 카메라에 투영한 후, 카메라 마다의 투영된 좌표를 연결하여 고차원 좌표를 구한다.

모든 $n$개의 점은 좌표 행렬 $K ∈ \mathbb R^{ 2n_c×n}$ 로 구성된 후, 공분산 행렬을 계산한다. 이때 $\bar K$는 투영된 모든 점의 평균 좌표이다.

공분산 행렬의 고유분해를 통해 고유벡터를 구하고, 이중 가장 큰 세 고유벡터로 구성한 행렬 $M' ∈ \mathbb R^{3×2n_c}$을 얻는다.(고유벡터 행렬에서 크다는 기준이 무엇인지?) 이 행렬 $M'$은 투영 축의 방향을 정의한다.

(추측) 해당 PCA를 통해 투영 축의 방향을 구하는 이유를 다음과 같이 생각해 볼 수 있다. 3D point $\mathbf x$를 projection matrix $P_i$를 통해 $C_i$로 투영하는 식을 $C_i(\mathbf x)=P_{i}\mathbf x$ 라고 할 때, 투영된 고차원의 좌표들을 $[P_1\mathbf x , ..., P_{n_c}\mathbf x]$ 로 볼 수 있다. 결국 해당 고차원 좌표의 PCA를 통해 고유 벡터를 얻는다는 것은 해당 영역의 카메라들의 projection matrix를 대표할 수 있는 벡터를 찾기 위함을 의미한다.

Computing the axis length

어느 한 점이 image space에서 한 픽셀(단위 길이) 정도 움직인다면 warp space에서도 마찬가지로 해당 공간의 단위 길이만큼 움직여야 한다. 따라서 위에서 정의한 행렬 $M'$ 의 각 축의 길이를 조정하기 위한 scale parameter $\{s_1, s_2, s_3\}$ 를 찾는다. $\{s_1, s_2, s_3\}$ 로부터 구성된 diagonal matrix(대각 행렬) $S ∈ \mathbb R^3$(대각행렬이면 $\mathbb R^{3×3}$이 아닌지?)를 통해 $M'$을 정규화할 수 있으며 이 정규화를 통해 처음 최소화하고자 했던 $M$을 구할 수 있다.

Jacobian matrix

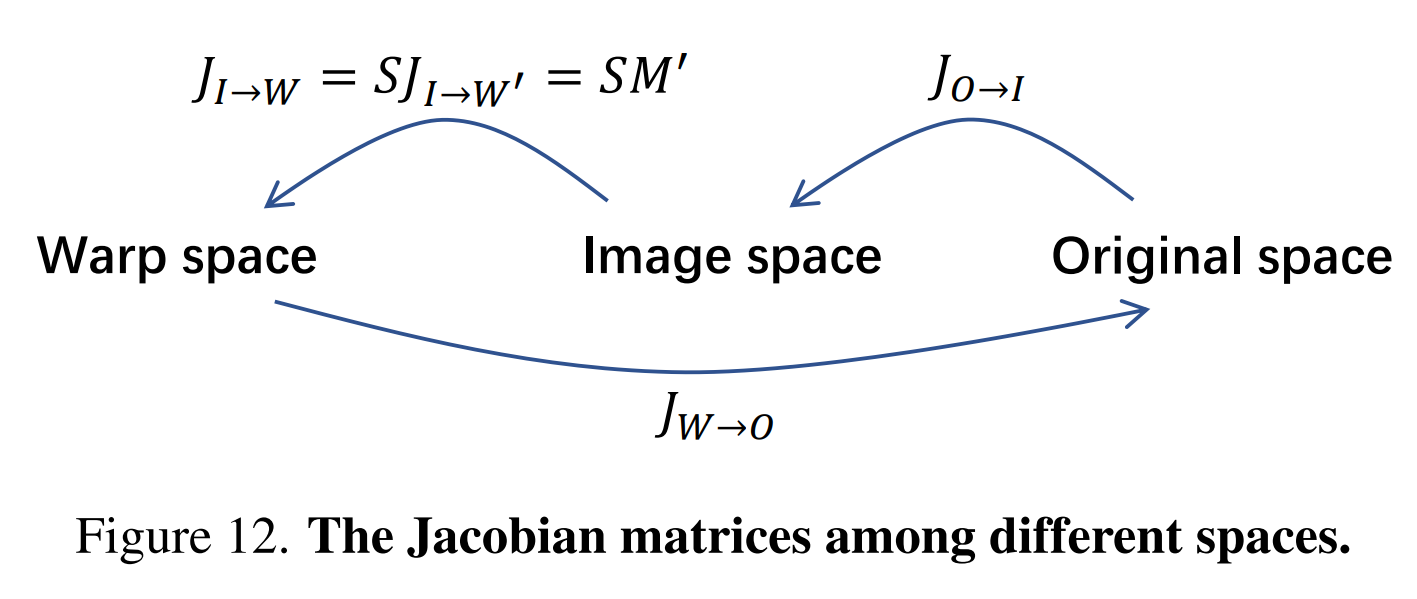
• original space에서 image space까지의 Jacobian 행렬 : $J_{O→I} ∈ \mathbb R^{3×2_{n_c}}$ (3D→2D를 위해선 $\mathbb R^{2_{n_c}×3}$이 아닌지?)
• image space에서 warp space까지의 Jacobian 행렬 : $J_{I→W} = M = SM'$

목표는 Jacobian 행렬 $J_{W→I} ∈ \mathbb R^{2_{n_c}×3}$ 을 계산하는 것이다. $J_{W→I}$ 는 정방행렬이 아니므로 $J_{I→W}$의 역으로 직접 계산할 수 없다. 이는 아래와 같이 더 자세히 표현할 수 있다.

$J_{W→I}$의 각 열 벡터의 최대값이 1이 되도록 scale parameter를 조정하여 점 $\mathbf x$에 대한 $\{s_1, s_2, s_3\}$ 값을 풀 수 있다. 모든 샘플링된 점 $\{\mathbf x_i\}$에 대해 최종 scale parameter로 $\{s_1, s_2, s_3\}$의 평균값을 사용한다.

이를 통해 제안된 각 node 마다의 perspective warping function인 $F(\mathbf x) = MG(\mathbf x)$을 계산할 수 있다. 실제 구현에서는 $F(\mathbf x)$에 대해 사후 정규화를 수행하여 warp space의 원점 주위(?)에 위치한 resulting point $\{\mathbf z_j\}$를 만든다.

Intuition of $F(\mathbf x)$

$F(\mathbf x)$는 original space 영역 $S$를 warp space의 원점 주변 영역에 매핑한다. 그림 4는 인접한 두 카메라 사이에서 서로 다른 각도로 뒤틀리는 perspective warping을 보여준다.

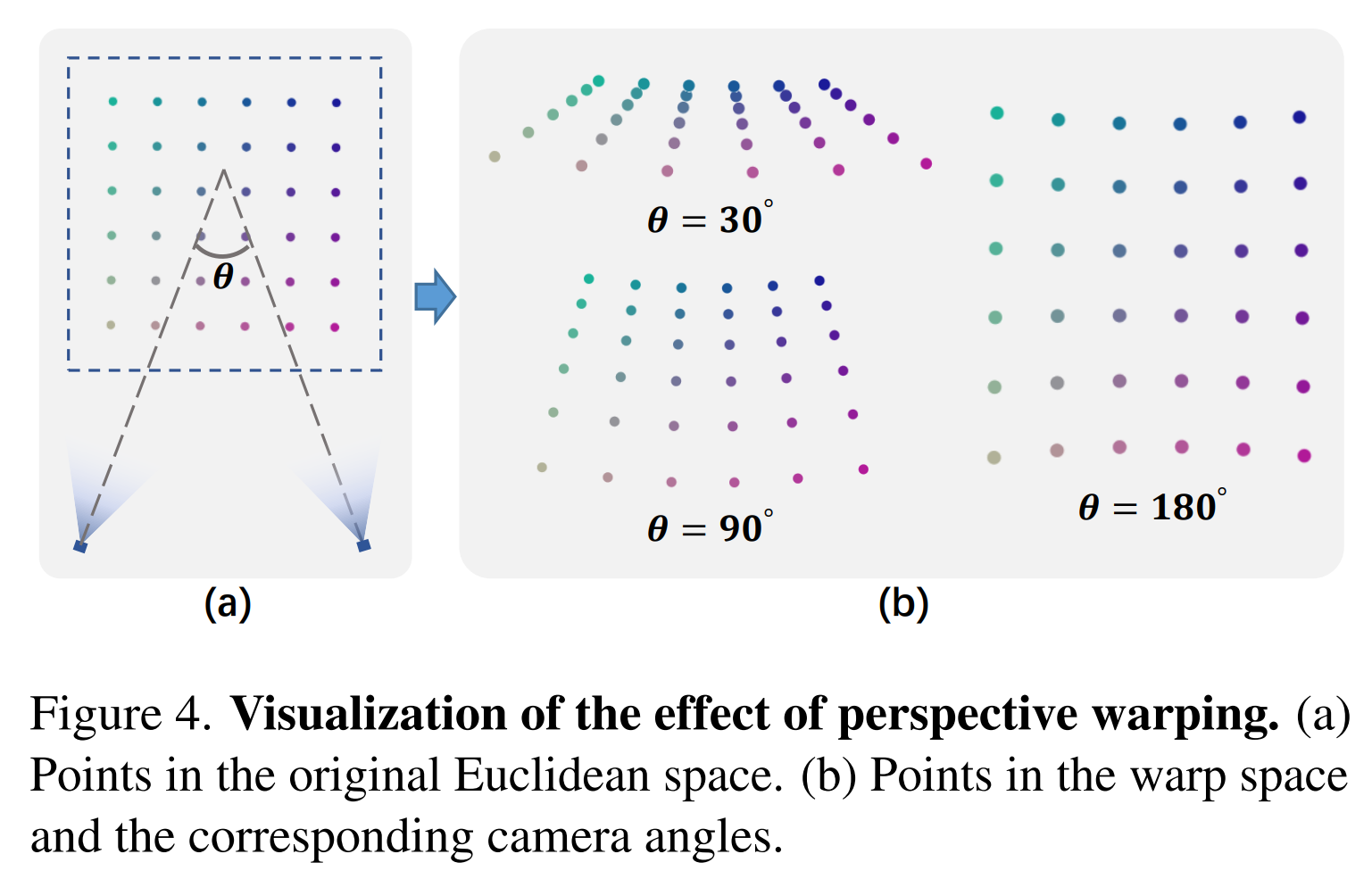
각도 $θ$가 작을수록 공간이 먼 영역에서 더 찌그러지며 이는 NDC warping과 유사하다. 각도가 커지면 warp space가 original Euclidean space과 더 유사하다. 모든 카메라가 정면을 향하고 있으면 perspective warping이 NDC warping과 유사하다.

Relationship with inverse sphere warping

Inverse sphere warping이 perspective warping function의 수동 근사치임을 경험적으로 보인다.

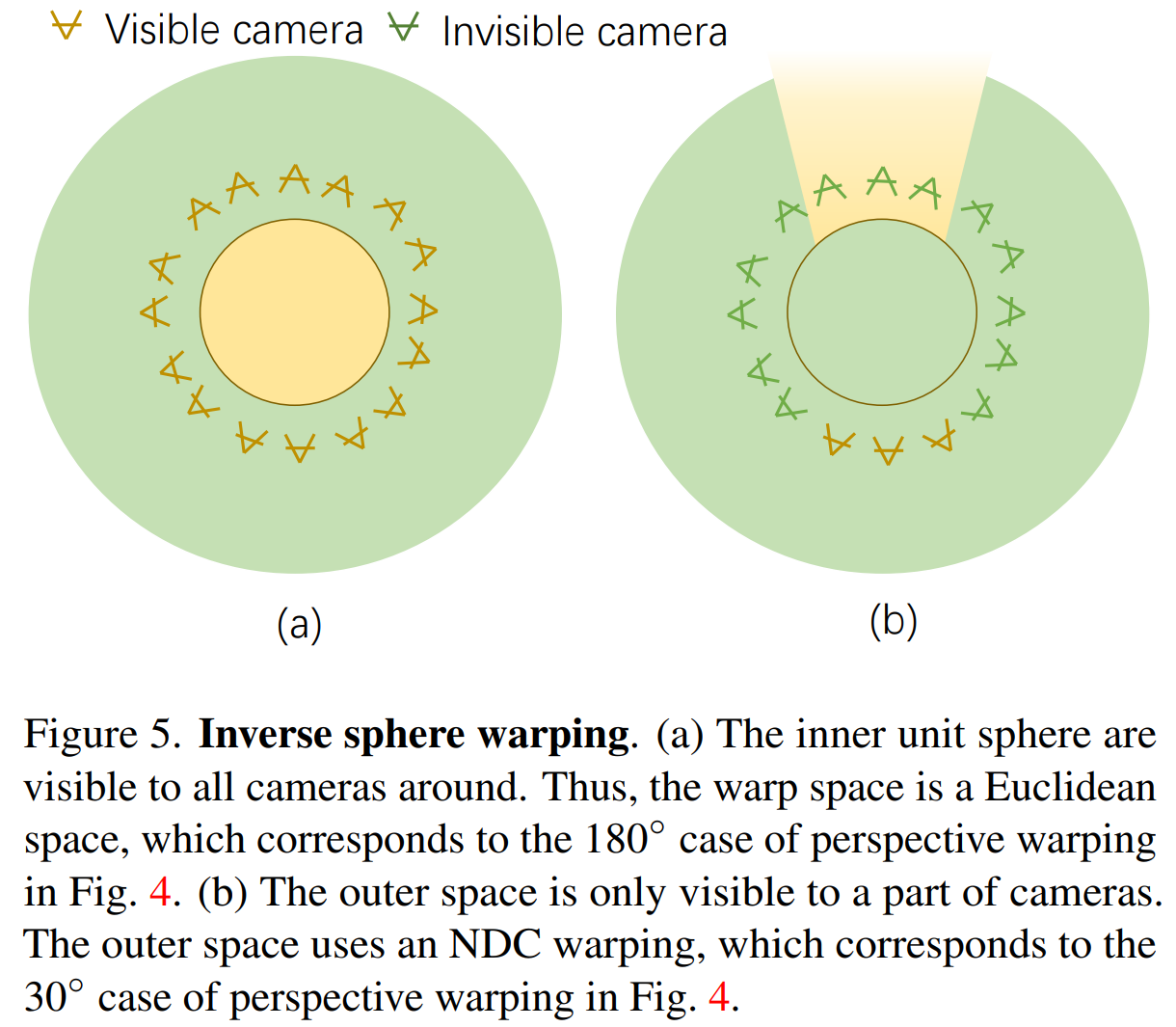
(a) 내부 단위 구에 대한 inverse sphere warping의 warp space는 이 단위 구에 주변의 모든 카메라가 보이기 때문에 original Euclidean space
→ perspective warping의 Fig. 4의 180° 케이스에 해당
(b) 외부 공간은 멀리 있는 몇 대의 카메라에서만 볼 수 있으므로 NDC warping과 유사하게 warping
→ perspective warping의 Fig. 4의 30° 케이스에 해당

3.3. Space subdivision

Perspective warping function $F(\mathbf x)$을 적용하기 위해서는 점 $\mathbf x$를 투영할 카메라를 지정해야 한다. 다만 free-trajectory scene에서는 특정 객체나 배경에 집중하는 카메라가 각자 다를 수 있다. 따라서 카메라에 따른 공간을 여러 영역으로 세분화하는 방법을 제안한다.

본 연구는 기본적으로 3D space를 octree로 구성한다. 어떤 카메라의 ray에서 샘플링된 점이 어떤 영역(voxel node)에 존재하면, 이 카메라를 해당 영역에서의 visible camera로 취급한다. 이 visible camera가 어떤 기준을 충족하면 공간을 세분화한다. 이후 각각의 세분화된 영역 $S_i$에 와핑 함수 $F_i(\mathbf x)$를 적용하여 $S_i$를 warp space에 매핑한다.

Subdivision strategy

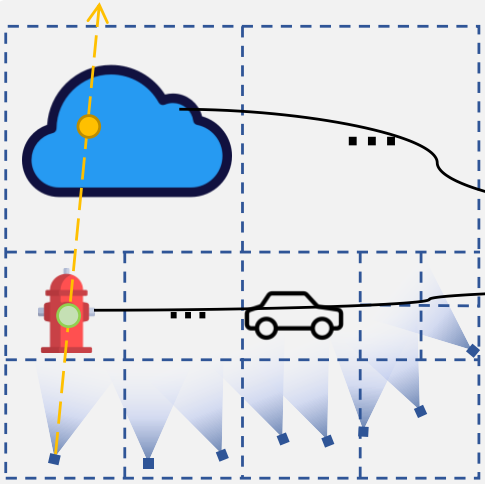
1. 3D space는 octree로 구성된다. 이 octree의 root node는 모든 카메라의 중심 위치를 포함하는 bounding box의 512배로 초기화된다. 이때 node의 측면 길이는 $s$이다.
2. 이 visible camera의 중심으로부터 node 중심까지의 거리를 $d$라고 할 때, $d ≤ λs$를 충족하면 측면 길이가 $s/2$ 인 8개의 sub node로 세분화된다. ($λ$는 3으로 설정)
3. $d$가 $λs$보다 더 크다면 해당 node와 카메라의 거리가 너무 멀기에(해당 node는 충분히 작으므로) 세분화를 멈추고 leaf node로 표시한다. 이 과정을 $n_l$개의 leaf node $\{S_i |i = 1, 2, ..., n_l\}$를 얻을 때까지 반복한다. 이때 $n_l$은 사전에 정한다.
4. 계산 효율을 위해 각 leaf node는 최대 4개의 visible camera를 가진다. node를 바라보는 카메라가 4개 보다 더 많으면 그 중 카메라를 랜덤으로 선택하고, 선택한 카메라와 가장 먼 카메라를 visible camera에 추가하는 과정을 4번 반복한다.

Camera rectification

Subdivision strategy을 통해 세분화된 leaf node $S$에 속한 visible camera의 보정 전략을 제안한다.

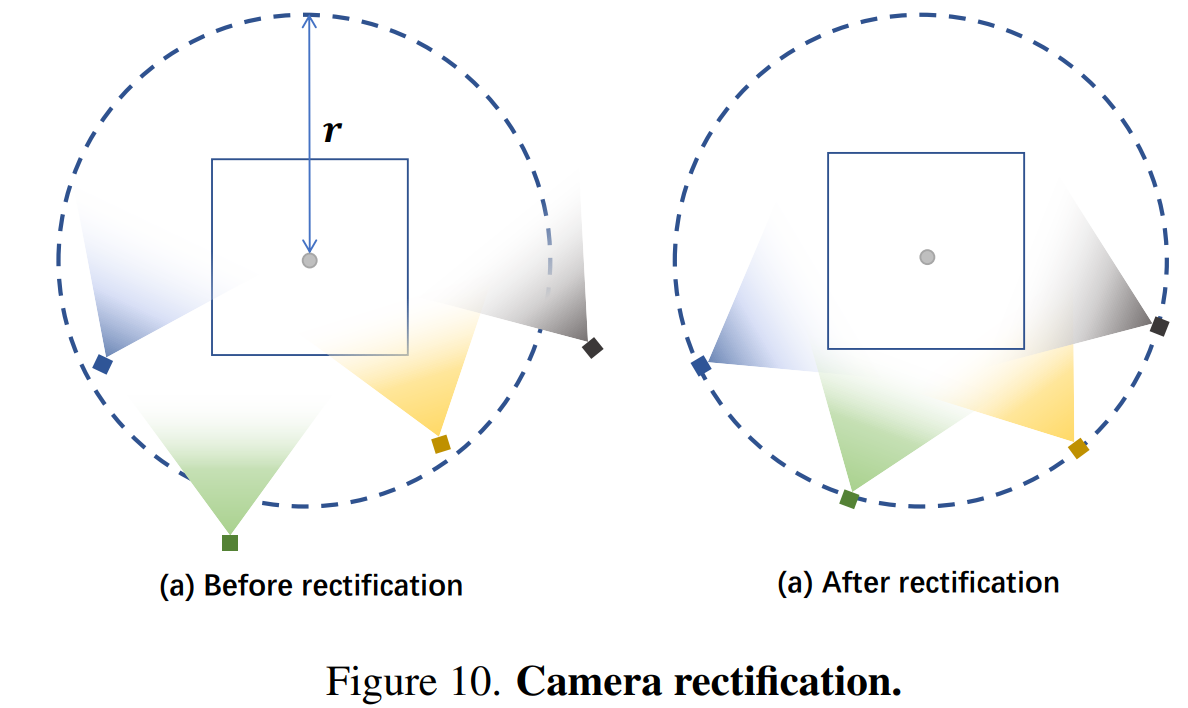
(a)와 같이 적절하지 않은 영역을 바라보는 일부 카메라는 perspective warping 계산에 직접 사용하기에 적합하지 않다. 따라서 카메라를 특정 거리에 위치시키고 카메라 view 방향을 회전하여 영역 $S$의 중심을 바라보게 하는 카메라 보정 전략을 제안한다. 이 방법은 $S$ 내부의 점이 의미 있는 좌표로 warping될 수 있도록 하는 데 도움을 준다. 이후 warping function $F_i$를 적용하면 각 leaf node는 warp space의 원점 주변 영역에 매핑된다.(?)

3.4. Scene representation

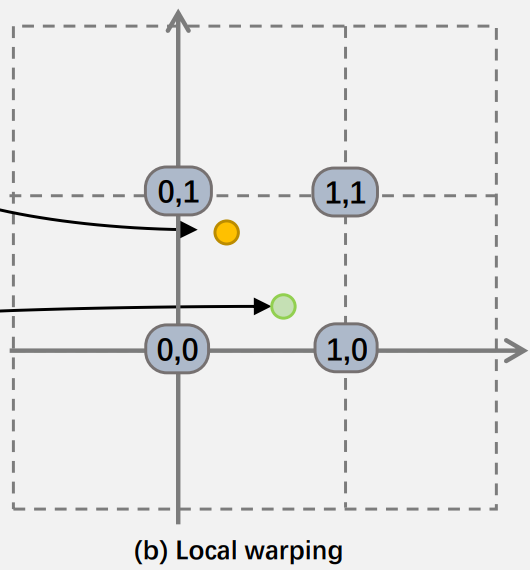
위에서 세분화된 각 leaf node에는 서로 다른 warping function이 적용되어 $n_l$개의 다른 warp space가 존재하게 된다. 이 warp space의 특정 지점에 대한 색상 및 밀도를 계산하는 naïve한 방법은 각 warp space에 $n_l$개의 다른 grid representation을 구축하는 것이다. 그러나 이것은 leaf node의 수에 따라 매개 변수의 수가 증가한다.

이를 해결하기 위해 warping function을 통해 동일한 서로 다른 leaf node를 같은 warp space에 매핑한다. 다만 두 leaf node가 동일한 warp space를 공유하면 밀도와 색상이 다른 두 point가 warp space의 동일한 지점에 매핑되어 충돌이 발생한다.

기존 Instant NGP에서는 하나의 hash function을 사용하지만, 본 연구는 이런 충돌 문제를 해결하기 위해 서로 다르지만 동일한 warp space에 매핑된 leaf node에 대해 서로 다른 hash function을 사용하여 hash-grid representation을 구축한다.

Hash grid with multiple hash functions

$i$번째 leaf node의 점 $\mathbf x$를 $\mathbf z = F_i(\mathbf x)$를 통해 warp space에 매핑하고 $\mathbf z$에 인접한 8개의 정수 좌표 grid vertex $\mathbf { \hat v}$를 찾는다. 이후 각 정수 vertex $\mathbf { \hat v}$에 대한 hash 값을 계산한다. 이때 서로 다른 숫자 $π_{i,k}$와 offset $Δ_{i,k}$을 사용하여 각 leaf node 마다 다른 hash function이 생성된다.

• $\oplus$ : bitwise xor operation
• $\{π_{i,k}\}$ & $\{\bigtriangleup_{i,k}\}$ : random large prime numbers $ offset
• $k = 1, 2, 3$ : index of $x, y, z$ coordinate of the warp space
• $L$ : length of the hash table

계산된 hash 값은 hash table을 indexing하는 데 사용되어 vertex $\mathbf { \hat v}$에 대한 feature vector를 검색한 후 8개의 vertex feature vector로부터 점 $\mathbf z$의 feature vector를 삼선 보간한다. 이후 point z에 대한 색상과 밀도를 생성하기 위해 $\mathbf z$의 feature vector와 view direction $\mathbf d$를 작은 MLP 네트워크로 공급한다.

서로 다른 leaf node의 두 점은 같은 warp space에서 동일한 vertex를 공유하지만 서로 다른 vertex feature vector를 탐색하므로 충돌 가능성이 줄어든다.

3.5. Perspective sampling

적절한 warp space에서 두 point 사이의 거리는 이미지 평면에 투영된 두 point 사이의 거리의 합과 같다(Definition 1). 이 definition에 따르면 original Euclidean space에서는 균일하지 않지만 warp space에서는 균일하게 샘플링할 수 있어 효율성을 향상시키고 보다 안정적인 수렴이 가능하다.

기존 NeRF에서의 샘플링 방법을 사용하여 얻은 첫번째 sample point가 $\mathbf x_i = \mathbf o + t_i\mathbf d$ 라면, 다음 sample point를 $\mathbf x_{i+1} = \mathbf x_i + δ_i\mathbf d$로 정의한다. 또한 warp space에서 균일하게 샘플링하기 위해 이 점들에 대해 perspective warping function $F$를 적용한다. 이 때 두점의 사이가 균일할 수 있도록 두 점의 거리를 $l$로 제한한다.

• $l$ : parameter controlling sample density($l = √3$, 즉 warp space에서 단위 큐브의 대각선 길이로 설정) → sampling 간격을 조정

Original space에서 효율적으로 marching step $δ_i$를 계산하기 위해 선형 근사를 통해 치환한다:

• $J_i$ : Jacobian matrix at $\mathbf x_{i}$ from the original space to the warp space

선형 근사치를 통해 구한 구한 $δ_i$를 통해 warp space에서 균일한 샘플링을 수행한다.

3.7. Training

Training loss

Color reconstruction loss

Regularization loss

• Disparity loss : disparity(inverse depth)가 지나치게 크지 않도록 하며 floating artifact를 줄임

  $\mathcal L_\text{Disp}=\frac{1}{n_r}\sum_k \text{disp}^2_k \tag 7$
  • 각 ray의 disparity는 샘플링된 inverse distance의 가중치 합으로 계산
  • $\text{disp}=\sum_{i}w_i \frac {1}{t_i}$ 와 $\{w_i\}$ : 볼륨 렌더링으로 계산된 가중치

• Total variance loss : 이웃한 두 octree nodes $i, j$의 경계에 있는 점들이 유사한 밀도와 색상을 갖도록 장려

  $\mathcal L_\text{TV}=\frac{1}{n_b}\sum_k \|\text{feat}^k_0-\text{feat}^k_1\|^2_2 \tag 8$
  • 이를 달성하기 위해, 각 training 반복에서 ocree node의 경계에서 $n_b = 8192$ 포인트를 무작위로 sampling
  • 각 샘플 포인트 $k$에 대해 $\text{feat}^k_0$과 $\text{feat}^k_1$은 인접한 두 octree node에 조건을 맞춘 두 가지 다른 함수를 사용하여 hash table에서 가져온 feature vector

• LLFF dataset : $λ_\text{Disp} = 2.5 × 10^{−4} , λ_\text{TV}= 10{−1}$

• Free, NeRF-360-V2 dataset : $λ_\text{Disp} = 10^{−3} , λ_\text{TV}= 10{−1}$

4. Experiments

4.1. Experimental Settings

Datasets

1. Free dataset : 자유 궤적을 가진 경계가 없는 7개의 수집 데이터 세트로, 긴 입력 카메라 궤적과 다중 초점 전경 객체가 있으므로 새로운 veiew 합성 작업을 위한 신경 표현을 구축하기 어려움
   

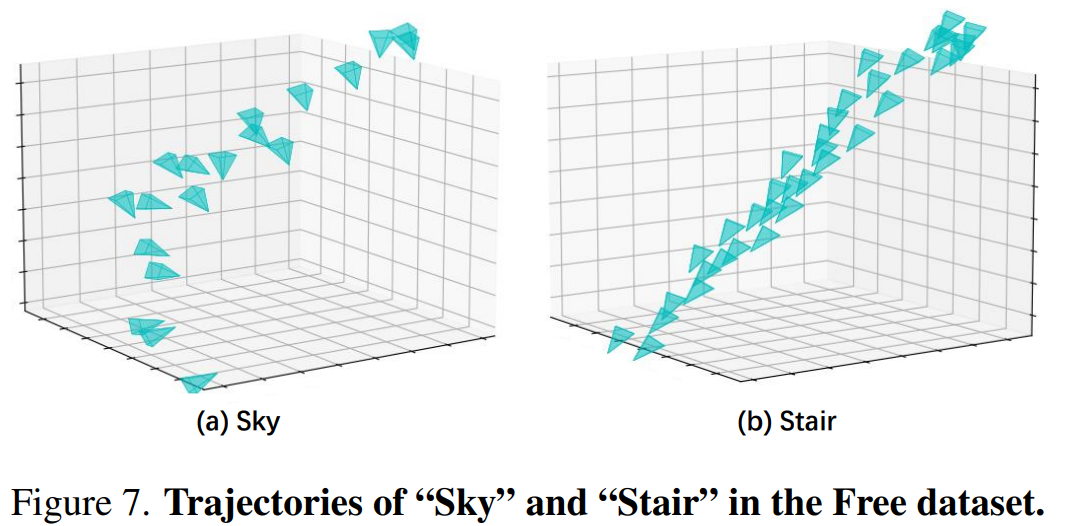
2. LLFF 데이터 세트 : 복잡한 기하학적 구조를 가진 8개의 실제 경계가 없는 전방 장면을 포함

3. NeRF-360-V2 데이터 세트 : 7개의 경계가 없는 360도 내부 및 실내 장면을 포함

• 여덟개 이미지 중 하나를 테스트, 나머지를 훈련 세트
• 평가 : PSNR, SSIM, LPIPSVGG

Baselines

(1) DVGO (2) 플레녹셀 (3) Instant-NGP와 비교

• NeRF++, 밉NeRF 및 밉-NeRF-360을 포함한 MLP 기반 NeRF 방법의 결과를 보고
• F2 -NeRF와 Instant-NGP는 모두 동일한 배치 크기로 20,000 단계 동안 훈련되었으며, LibTorch를 사용
• 모든 훈련 시간은 단일 2080Ti GPU에서 평가

Warping functions

• LLFF 데이터 세트에서는 모든 baseline이 NDC warping function을, Free 데이터 세트와 NeRF-360-V2 데이터 세트 모두에서 Instant-NGP를 제외한 모든 baseline 방법은 inverse sphere warping function을 사용
• Instant-NGP에서는 공식 구현을 따라 ray marching bounding box를 확대하여 배경을 나타내고, 다양한 장면에서 최상의 성능을 달성하기 위해 scale 매개 변수를 조정하기 위해 공식 구현 따름
• F$^2$-NeRF는 모든 데이터 세트에 대해 항상 perspective warping 사용

Architecture details

• Instant-NGP와 유사한 설정 : 16개 레벨의 해시 테이블을 사용하며, 각 레벨은 2차원의 $2^{19}$개 feature vector를 포함
• 크기 32 fetched hash feature vector는 너비 64 hidden layer가 있는 작은 MLP로 공급되어 장면 특징과 볼륨 밀도를 얻음
• scene feature는 뷰 방향의 spherical harmonics encoding과 연결하고 너비 64의 두 개의 hidden layer를 가진 다른 렌더링 MLP로 공급되어 RGB 색상을 얻음

Training details

• Instant-NGP를 따르고 포인트 샘플의 고정 배치 크기를 256k로 설정하는 반면, 광선의 배치 크기는 광선의 평균 샘플링 포인트에 따라 동적
• optimizer : Adam
• learning rate : 처음 1k 단계에서는 0에서 $1 × 10^{−1}$로 선형적으로 증가하고 cosine scheduling을 사용하여 훈련이 끝나면 $10^{−2}$로 감소

Cosine annealing
학습율의 최대값과 최소값을 정해서 그 범위의 학습율을 코싸인 함수를 이용하여 스케쥴링하는 방법

• iteration : 20,000
• LibTorch를 사용하여 F$^2$ -NeRF 구현
• 훈련 시간은 장면의 복잡성에 따라 다르며, 대부분의 경우 단일 Nvidia 2080Ti GPU에서는 10분에서 15분 사이

4.2. Comparative studies

Free 데이터셋에 대한 정량적 비교 결과

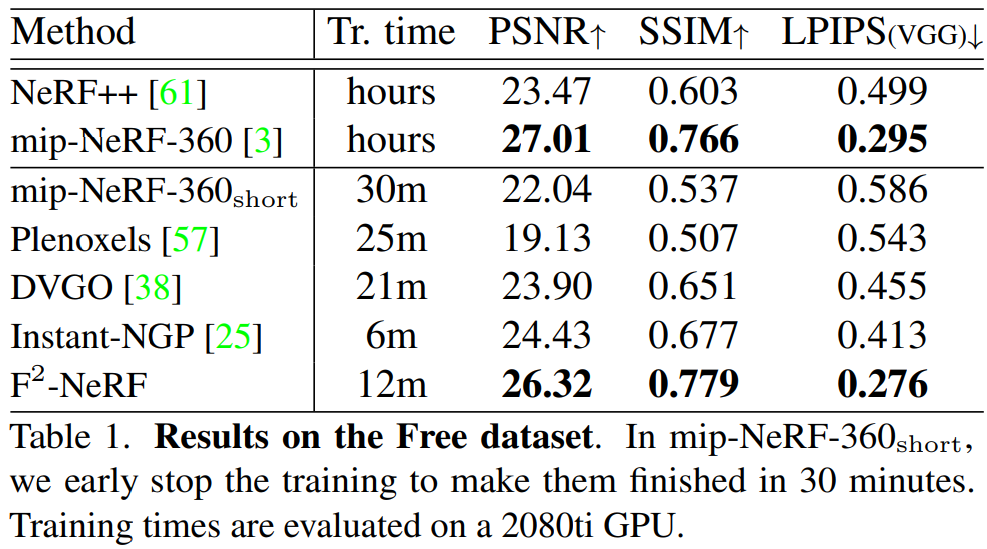
• F2-NeRF는 빠른 NeRF 중에서 최고의 렌더링 품질 달성

Free 데이터셋에 대한 정성적 비교 결과

• DVGO 및 Plenoxels : 긴 궤적을 나타내기에는 해상도가 제한적이기 때문에 흐릿
• Instant-NGP : 더 날카로워 보이나, 불균형한 장면 공간 구성 때문에 명확하지 않음
• F2-NeRF : perspective warping과 적응적 space subdivision을 활용하여 표현 능력을 최대한 활용하므로 더 나은 렌더링 품질
• mip-NeRF-360 : Free 데이터셋에서 오랫동안 훈련시키면 명확한 이미지를 렌더링할 수도 있다는 것을 발견
  → 이는 훈련 과정에서 사용되는 대규모 MLP 네트워크가 점차 전경 객체에 집중하고 이 객체에 더 많은 용량을 동적으로 할당할 수 있기 때문
  → 그러나 이러한 MLP 네트워크들은 Free Trajectory 데이터셋에서 수렴을 위해 오랜 시간을 소비
• mip-NeRF-360(짧은 시간(30분) 훈련) : 안개 같은 아티팩트 포함

데이터셋 LLFF와 NeRF-360-V2에서의 평가

Perspective warping이 특수화된 카메라 궤적과 호환되는지를 보여주기 위해 forward-facing dataset(LLFF) 및 360◦ object-centric datase(NeRF-360-V2)에서 평가

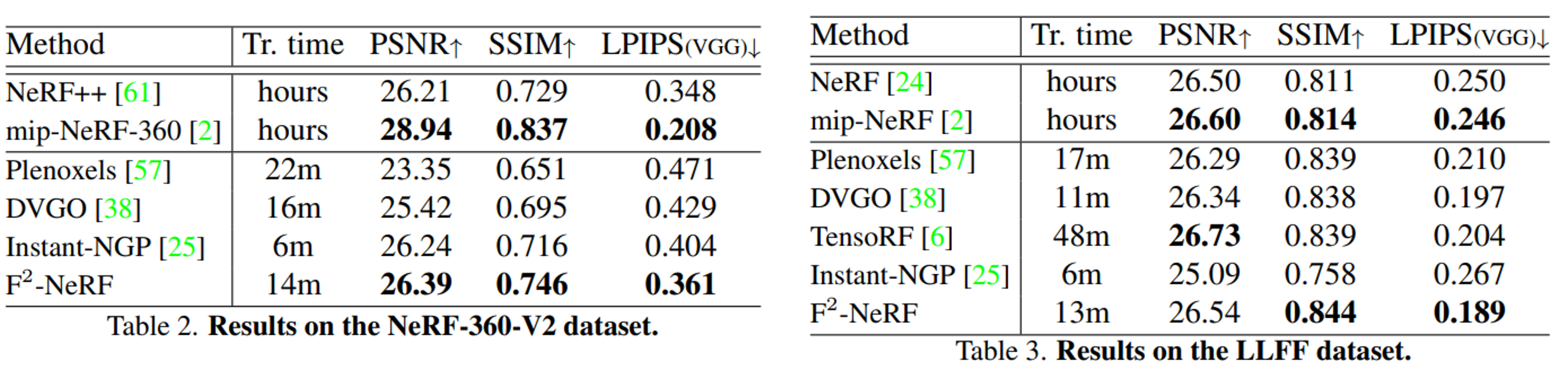
• 두 데이터셋 모두에서 F2-NeRF는 다른 빠른 NeRF 방법과 유사한 결과 달성
• 기존 빠른 NeRF baseline 방법들은 두 데이터셋에 대해 특별히 설계된 NDC warping 또는 inverse sphere warping을 채용하는 반면, F2-NeRF는 모든 데이터셋에 대해 항상 동일한 perspective warping 사용

4.3. Ablation studies

"pillar"라는 장면을 대상으로 ablation study를 수행

• multi-resolution hash grid를 scene representation으로 사용하고 warping function과 샘플링 전략을 변경
• warping function : inverse sphere warping (Inv. warp), perspective warping (Pers. warp), no warping (w/o warp) 사용
  → Free 데이터셋에서 inverse sphere warping을 구현할 때, 모든 카메라 위치의 bounding sphere를 전경 내부 구로 사용하고 구 바깥 공간을 배경으로 취급
• 샘플링 전략 : mip-NeRF-360의 disparity (inverse-depth) 샘플링 (Disp. Sampling), InstantNGP 의 exponential function 샘플링 (Exp. Sampling), 본 연구의 원근 샘플링

• A) warping 없이 disparity sampling을 사용하는 모델로 성능이 가장 나쁨
• B) Inv. warping을 사용하는 모델로 결과가 향상되어, (A)와 비교하면 무한한 장면과 더 호환성이 높은 것을 보임
• C) exponential sampling으로 disparity sampling을 대체하며 결과가 더 좋아짐
• D) 제안된 perspective warping을 사용하며, 역 구 형태 구 왜핑과 비교하여 성능이 급격히 향상
  → perspective warping이 자유 궤적에서의 효과를 입증
• E) (D)에 원근 샘플링을 적용하며 가장 우수한 성능

Reference

• https://xoft.tistory.com/41
• https://www.youtube.com/watch?v=mrRQ-6iC9xA