⚡ 백트래킹
📌 백트래킹(Backtracking)
- 여러 가지 선택지(옵션)들이 존재하는 상황에서 한가지를 선택한다.
- 선택이 이루어지면 새로운 선택지들의 집합이 생성된다.
- 이런 선택을 반복하면서 최종 상태에 도달한다.
- 올바른 선택을 계속하면 목표 상태(goal state)에 도달한다.
🔷 백트래킹과 깊이 우선 탐색과의 차이
- 어떤 노드에서 출발하는 경로가 해결책으로 이어질 것 같지 않으면 더 이상 그 경로를 따라가지 않음으로써 시도의 횟수를 줄임.
💡
Prunning(가지치기) 라고 한다.
- 깊이 우선 탐색이 모든 경로를 추적한다면 백트래킹은 유망성 검사를 통해 불필요한 경로를 조기에 차단한다.
❗ 깊이 우선 탐색을 가하기에 경우의 수가 너무 많을 때 가장 바람직하지만 최악이 경우에는 여전히 지수함수 시간을 요하므로 처리가 불가능할 수 있다.
🔷 N-Queen 문제
-
NxN 서양 장기판에서 배치한 Queen들이 서로 위협하지 않도록 n개의 Queen을 배치하는 문제
어떤 두 Queen도 서로를 위협하지 않아야한다. 이 때, Queen을 배치한 n개의 위치는?
-
완전탐색은 해답이 될 가능성이 전혀 없는 노드의 후손 노드들도 전부 탐색하기 때문에 굉장히 비효율적인 방식이 된다.
-
어떤 노드의 유망성을 점검한 후에 유망(
promising)하지 않다고 결정되면 그 노드의 부모로 되돌아가(backtracking)다음 자식 노드로 간다. -
어떤 노드를 방문하였을 때 그 노드를 포함한 경로가 해답이 될 수 없으면 그 노드는 유망하지 않다고 하며, 반대로 해답의 가능성이 있으면 유망하다고 한다.
🌟 백트래킹에 정해진 정답은 없다!
📌 순열(Permutation)
🔷 서로 다른 것들 중 몇 개를 뽑아서 한 줄로 나열하는 것
- 서로 다른 n개 중 r개를 택하는 순열: nPr
💡 nPr은 다음과 같은 식이 성립한다.
nPr = n x (n-1) x (n-2) x ... x (n-r+1)
nPn = n!(Factorial)
-
다수의 알고리즘 문제들은 순서화된 요소들의 집합에서 최선의 방법을 찾는 것과 관련 있다.
-
N개의 요소들에 대해서 n! 개의 순열들이 존재한다.
-
사전적 순서도 있지만 최소 변경을 통한 방법도 있다.
💡 각각의 순열들은 이전의 상태에서 단지 두 개의 요소들 교환을 통해 생성된다는 점을 이용한다.
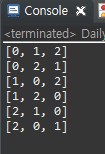
🖥 최소 변경을 통한 순열 출력(swap)
import java.util.Arrays;
public class DailyClass {
public static int [] nums; // 배열
public static int N; // 원소수
public static void main(String[] args) {
nums = new int[] {0,1,2};
N = nums.length;
perm(0);
}
// 최소 변경을 통한 순열 출력
// idx: 현재 판단 위치
public static void perm(int idx) {
// 기저조건
if(idx == N) {
System.out.println(Arrays.toString(nums));
return;
}
// 재귀조건
for(int i = idx; i < N; i++) {
swap(i, idx);
perm(idx+1);
swap(i, idx);
}
}
// nums 배열을 static하게 처리 했기 때문에 매개변수로 받지 않아도 처리 가능
public static void swap(int a, int b) {
int tmp = nums[a];
nums[a] = nums[b];
nums[b] = tmp;
}
}
🖥 최소 변경을 통한 순열 출력(방문 체크)
import java.util.Arrays;
public class DailyClass {
public static int [] nums; // 배열
public static int N; // 원소수
public static int [] result; // 결과저장
public static boolean[] visited; // 해당 원소 사용 유무
public static void main(String[] args) {
nums = new int[] {0,1,2};
N = nums.length;
result = new int[N];
visited = new boolean[N];
perm(0);
}
// 최소 변경을 통한 순열 출력
// idx: 현재 판단 위치
public static void perm(int idx) {
// 기저조건
if(idx == N) {
System.out.println(Arrays.toString(result));
return;
}
// 사용할 수 있는 모든 원소 체크
for(int i = 0; i < N; i++) {
if(visited[i]) continue; // 이미 사용한 원소일 때 생략
result[idx] = nums[i]; // 해당 i번째의 원소를 저장
visited[i] = true; // i번째 원소 사용했다고 표시
perm(idx+1);
visited[i] = false; // i번째 원상복구
}
}
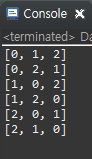
}🌟 비트마스킹을 활용할 수도 있다.
import java.util.Arrays;
public class DailyClass {
public static int [] nums; // 배열
public static int N; // 원소수
public static int [] result; // 결과저장
public static void main(String[] args) {
nums = new int[] {0,1,2};
N = nums.length;
result = new int[N];
perm(0, 0);
}
// 최소 변경을 통한 순열 출력
// idx: 현재 판단 위치
// 인자를 통한 비트마스킹을 하면 일회성으로 이용 가능하기 때문에 visited 배열 선언보다 효율적이다
public static void perm(int idx, int visited) {
// 기저조건
if(idx == N) {
System.out.println(Arrays.toString(result));
return;
}
// 사용할 수 있는 모든 원소 체크
for(int i = 0; i < N; i++) {
// 해당 원소를 썼는지 체크
if((visited & (1<<i)) > 0) continue;
result[idx] = nums[i]; // 결과저장
perm(idx+1, visited | (1 << i));
}
}
}
❗ 중복된 값이 포함된 배열의 순열을 체크할 때 같은 순열을 중복 출력할 수 있다. 이 때는
next_permutation을 사용할 수 있다. 이건 나중에 알아보자.