⚡ 그래프 (1)
📌 그래프(Graph)
🔷 아이템(사물 또는 추상적 개념)들과 이들 사이의 연결 관계 표현
정점(Vertex)들의 집합과 이들을 연결하는간선(Edge)들의 집합으로 구성된 자료구조- 선형자료구조나 트리자료구조로 표현하기 어려운 M:N관계를 표현
⭐ 그래프의 종류
-
완전 그래프
- 정점들에 대해 가능한 모든 간선들을 가진 그래프
- 간선의 개수 =
N(N-1)/2
-
부분 그래프
- 원래 그래프에서 일부의 정점이나 간선을 제외한 그래프
-
무향 그래프(Undirected Graph)
- 간선의 방향이 없다.
-
유향 그래프(Directed Graph)
- 간선의 방향이 존재한다.
-
가중치 그래프(Weighted Graph)
- 간선에 값을 부여한 그래프
-
순환 그래프(Cylcle graph)
- 사이클이 있는 그래프
-
사이클 없는 방향 그래프(DAG, Directed Acyclic Graph)
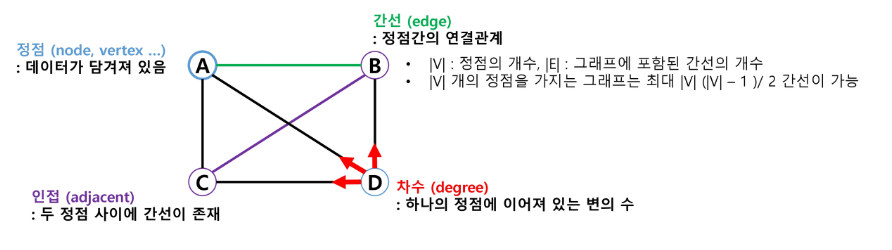
⭐ 인접 정점
🔷 인접(Adjacency)
- 두 개의 정점에 간선이 존재(연결됨)하면 서로 인접해 있다고 한다.
- 완전 그래프에 속한 임의의 두 정점들은 모두 인접해 있다.
⭐ 그래프 경로
🔷 경로(Path)
- 간선들을 순서대로 나열한 것
- 경로 중 한 정점을 최대한 한번만 지나는 경로를
단순경로라 한다. - 시작한 정점에서 끝나는 경로를
사이클(Cycle)이라고 한다.
📌 그래프 표현
🔷 간선의 정보를 저장하는 방식, 메모리나 성능을 고려해서 결정
- 인접 행렬
- |V| X |V| 크기의 2차원 배열을 이용해서 간선 정보를 저장
- 배열의 배열
- 인접 리스트
- 각 정점마다 해당 정점으로 나가는 간선의 정보를 저장
- 간선의 배열
- 간선(시작 정점, 끝 정점)을 배열에 연속적으로 저장
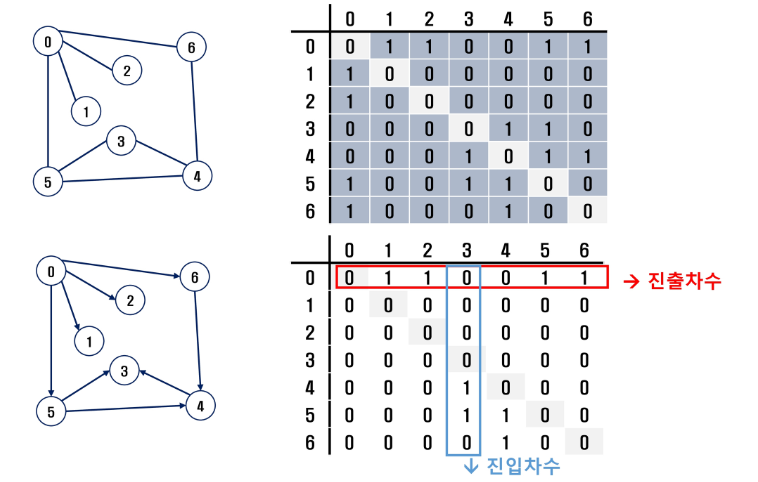
⭐ 인접 행렬
-
두 정점을 연결하는 간선의 유무를 행렬로 표현
-
|V| X |V| 정방 행렬 (2차원 배열)
-
행 번호와 열 번호는 그래프의 정점에 대응
-
두 정점이 인접되어 있으면 1, 그렇지 않으면 0으로 표현
❗ 시작 정점이 0인지 1인지가 중요하다. 이는 문제를 통해 확인하거나 문제의 input case로 확인한다.
🔷 무향 그래프
- i번째 행의 합 = i 번째 열의 합 = Vi의 차수
🔷 유향 그래프
- 행 i의 합 = Vi의 진출 차수
- 열 i의 합 = Vi의 진입 차수
🔷 단점
간선이 적을 때 낭비되는 메모리 공간이 많다.
import java.util.Scanner;
public class DailyAPS {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
//정점의 개수(V)와 간선의 수(E)가 주어진다.
int V = sc.nextInt();
int E = sc.nextInt();
//인접행렬
int [][] adjArr = new int[V+1][V+1]; // 1번~V개의 정점 번호를 이용한다라고 가정
//간선 정보 입력
for(int i = 0; i < E; i++) {
int A = sc.nextInt(); //시작정점
int B = sc.nextInt(); //끝정점
int w = sc.nextInt(); //가중치 그래프라고 했을 때 가중치 값
adjArr[A][B] = w; //가중치가 있을 때 w, 없다면 1
adjArr[B][A] = w; //무향일 때 필수, 유향일 때 생략
// adjArr[A][B] = adjArr[B][A] = w; //정리 표현
}
}
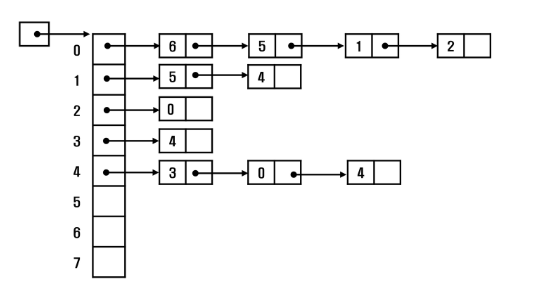
}⭐ 인접 리스트
- 각 정점에 대한 인접 정점들을 순차적으로 표현
- 하나의 정점에 대한 인접 정점들을 각각 노드로 하는 연결 리스트로 저장
🔷 무향 그래프
- 노드 수 = 간선의 수 * 2
- 각 정점의 노드 수 = 정점의 차수
🔷 유향 그래프
- 노드 수 = 간선의 수
- 각 정점의 노드 수 = 정점의 진출 차수
🔷 단점
탐색하는 시간이 인접 행렬에 비해 길어진다.
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class DailyAPS {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
//정점의 개수(V)와 간선의 수(E)가 주어진다.
int V = sc.nextInt();
int E = sc.nextInt();
//인접리스트
List<Integer>[] adjList = new ArrayList[V + 1];
//ArrayList를 초기화해주지 않으면 Null값으로 남아있게 되므로 초기화
for(int i = 0; i < V+1; i++) {
adjList[i] = new ArrayList<>();
}
//간선 정보 입력
for(int i = 0; i < E; i++) {
int A = sc.nextInt(); //시작정점
int B = sc.nextInt(); //끝정점
int w = sc.nextInt(); //가중치 그래프라고 했을 때 가중치 값
adjList[A].add(B);
adjList[B].add(A);//무향 그래프일 때 필수
}
}
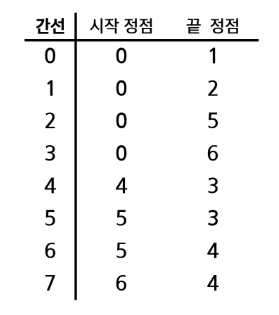
}⭐ 간선 배열
- 정점과 정점의 연결 정보인 간선을 배열에 저장
- 간선을 표현하는 두 정점의 정보를 배열 혹은 객체로 저장할 수 있음.
import java.util.Scanner;
public class DailyAPS {
static class Edge {
int st, ed;
public Edge(int st, int ed) {
this.st = st;
this.ed = ed;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
//정점의 개수(V)와 간선의 수(E)가 주어진다.
int V = sc.nextInt();
int E = sc.nextInt();
//간선배열 1 (2차원 배열 활용)
int [][] edges1 = new int[E][3]; // [i][0]: 시작정점, [i][1]: 끝정점, [i][2]: 가중치
//간선배열 2 (시작정점과 끝정점을 담은 간선 객체 활용)
Edge[] edges2 = new Edge[E];
for(int i = 0; i < E; i++) {
int A = sc.nextInt();
int B = sc.nextInt();
int w = sc.nextInt();
edges2[i] = new Edge(A, B); //간선 정보자체를 배열로 저장하기 때문에 유향/무향은 상관 없다
}
}
}