---

⚡ 그래프 (2)

---

📌 그래프 탐색

🔷 트리(그래프, 2차원 배열) 순회(탐색)

• 모든 자료를 빠짐 없이 탐색하는 것

⭐ 깊이 우선 탐색 (Depth First Search, DFS)

🔷 루트 노드(시작 정점, 출발 위치)에서 출발하여 한 방향으로 갈 수 있는 경로가 있는 곳까지 깊이 탐색해 가다가 더 이상 갈 곳이 없게 되면, 가장 마지막에 만났던 갈림길 간선이 있는 노드(정점)로 되돌아와서 다른 방향의 노드(정점)으로 탐색을 계속 반복하여 결국 모든 노드(정점)을 방문하는 순회방법

• 가장 마지막에 만났던 갈림길의 노드(정점)로 되돌아가서 다시 깊이 우선 탐색을 반복해야 하므로 후입선출(LIFO) 자료구조인 스택 사용
• 재귀 함수는 시스템 스택을 이용하므로 이를 이용하여 간단하게 구현할 수도 있다.

🔷 탐색 방법(stack)
1) 루트 노드를 stack에 push한다.
2) stack에서 노드(curr)를 pop한다.
3) curr의 모든 자식 노드를 stack에 push한다.
4) stack이 공백 상태가 될 때까지 2)-3)을 반복한다.

🔷 탐색 방법(재귀 함수)
1) 현재 노드(V) 방문
2) (V)의 자식 노드 (W)를 차례로 재귀 호출

❗ 재귀로 그래프 탐색 시 주의점
1. 트리와 다르게 그래프 탐색 시에는 탐색한 곳을 되돌아가 중복 탐색할 수 있다. 무한 재귀 지옥에 빠질 수 있으므로 visited 처리를 위한 boolean 배열을 따로 선언하여 사용해주자.
2. 인접 행렬 탐색시 범위 체크 중 배열 범위를 벗어날 수 있다. 오류 방지를 위해 2차원 배열의 x, y를 1씩 더 크게 선언한 뒤에 탐색하지 않게 하는 임의의 값을 넣으면 편리하다.

public class DailyAPS {
	static int N = 7;
	//인접 행렬
	static int [][] adj = {
			{ 0, 1, 1, 0, 0, 1, 0 },
			{ 1, 0, 0, 1, 0, 0, 1 },
			{ 1, 0, 0, 1, 0, 0, 0 },
			{ 0, 1, 1, 0, 0, 0, 1 },
			{ 0, 0, 0, 0, 0, 1, 1 },
			{ 1, 0, 0, 0, 1, 0, 0 },
			{ 0, 1, 0, 1, 1, 0, 0 }
	};
	
	static boolean[] visited = new boolean[N]; //방문처리를 할 배열
	
	public static void main(String[] args) {
		DFS(2);
	}
	
	//인자로 현재 내가 방문하고 있는 정점이 들어온다.
	static void DFS(int v) {
		//v에 대한 방문처리
		visited[v] = true;
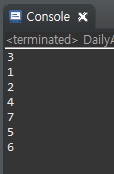
		System.out.println(v+1); //그래프가 1부터 시작한다고 가정하고 1을 더했다
		
		//방문하지 않았으면서, 연결된 간선이 존재한다면 재귀 호출
		for(int i = 0; i < N; i++) {
			if(!visited[i] && adj[v][i] == 1) {
				DFS(i);
			}
		}
	}
}

⭐ 너비 우선 탐색 (Breadth First Search, BFS)

🔷 루트 노드(시작 정점, 출발 위치)의 자식 노드(인접한 정점)들을 먼저 모두 차례로 방문한 후에 방문했던 자식 노드들(인접한 정점)을 시작점으로 하여 다시 해당 노드의 자식 노드(인접한 정점)들을 차례로 방문하는 방식

• 자식 노드(인접한 정점)들에 대해 탐색을 한 후, 차례로 다시 너비 우선 탐색을 진행해야 하므로, 선입선출(FIFO) 자료구조인 큐를 활용
• 너비 우선 탐색은 인접한 노드들 부터 차례대로 방문을 하므로 시작 정점과 끝 정점이 주어졌을 때 최단 길이를 구할 수 있다.

🔷 탐색 방법(queue)

1) 루트 노드를 queue에 삽입
2) queue에서 원소(curr) 꺼내기
3) 해당 원소 방문 처리
4) curr의 자식 노드를 queue에 삽입
5) queue가 공백이 될 때까지 2)~5) 반복

import java.util.LinkedList;
import java.util.Queue;

public class DailyAPS {
	static int N = 7;
	//인접 행렬
	static int [][] adj = {
			{ 0, 1, 1, 0, 0, 1, 0 },
			{ 1, 0, 0, 1, 0, 0, 1 },
			{ 1, 0, 0, 1, 0, 0, 0 },
			{ 0, 1, 1, 0, 0, 0, 1 },
			{ 0, 0, 0, 0, 0, 1, 1 },
			{ 1, 0, 0, 0, 1, 0, 0 },
			{ 0, 1, 0, 1, 1, 0, 0 }
	};
	
	static boolean[] visited = new boolean[N]; //방문처리를 할 배열
	static Queue<Integer> queue = new LinkedList<Integer>();
	
	public static void main(String[] args) {
		BFS(0); 
	}
	//v: 시작정점
	static void BFS(int v) {
		//시작정점을 큐에 넣는다.
		queue.add(v);
		visited[v] = true; //방문처리
		
		//큐가 공백이 될 때까지 반복
		while(!queue.isEmpty()) {
			//정점을 하나 꺼낸다
			int t = queue.poll();
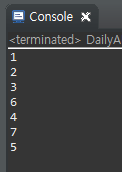
			System.out.println(t+1); //1부터 시작한다고 가정
			
			//t와 연결되어 있으면서 방문하지 않는 정점들은 queue에 넣고 방문처리를 한다
			for(int i = 1; i < N; i++) {
				if(!visited[i] && adj[t][i] == 1) {
					queue.add(i); //큐에 넣고 방문처리
					visited[i] = true;
				}
			}
		}
	}
}

🔷 최단 길이 구하는 방법
1) 2차원 배열을 만들어 직접 길이를 저장한다.
2) 큐에 넣을 때 같이 넣어 저장한다. (큐 생성시 Integer[]로 생성 or 클래스 멤버 변수로 함께 저장)
3) 길이를 저장하는 변수를 생성하여 이를 활용한다. (Queue size를 묶어 같은 레벨끼리 처리)

---

중요 파트!