논문 제목 : Densely Connected Convolutional Networks
논문 링크 : https://arxiv.org/pdf/1608.06993.pdf
이번에 리뷰할 논문은 DenseNet이다.
Abstract
기존의 신경망이 L개의 layer가 있을 때 L개의 connection이 있다면,
DenseNet은 개의 connection이 있다.
How?
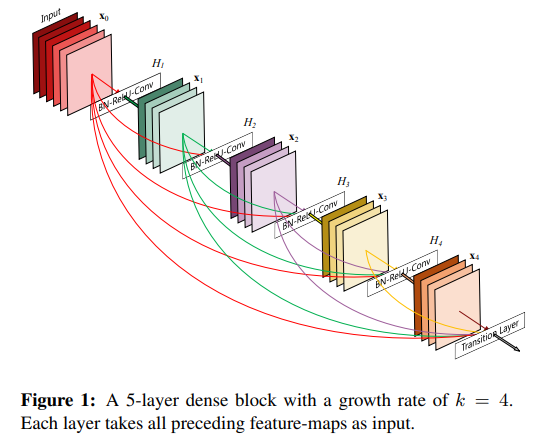
Fig. 1을 참고하자. L개의 layer가 있다면 이다.
첫 시작이 L인 이유는 input부터 모든 layer에 connection이 생기기 때문이다.
이러한 DenseNet은 아래와 같은 장점을 지닌다.
- 기울기 소실 문제 감소
- 견고한 feature propagation
- feature 재사용 장려
- parameter 수 감소
1. Introduction
CNN이 출연함에 따라 발전이 이어졌지만, 진짜 deep한 CNN은 최근에야 등장했다.
LeNet5는 layer가 5개뿐이고, VGG는 19개다.
(이 당시)오직 Highway Network와 ResNet만이 100개의 layer를 넘었다.
CNN이 깊어짐에 따라 input의 정보가 사라진다(wash out)는 문제가 있다.
이를 해결하기 위해
- ResNet과 Highway Network는 small connection을 만들어 layer간 signal pass를 만들었다.
- ResNet은 information과 gradient flow를 더 잘하게 하기 위해 확률적으로 layer를 drop해 Stochastic depth shorten을 했다.
- FractalNet은 많은 short path를 가진채로 깊은 depth를 유지하기 위해, 여러 개의 parallel layer sequence를 서로 다른 수의 convolutional block과 결합했다.
이러한 방법에는 공통적 특징이 있다 : layer 간 short path를 만드는 것이다.
이 논문에서 저자는 이러한 통찰을 녹여내며, maximum information flow를 보장하기 위해 모든 layer를 connect했다.
기존의 network들이 L-layer일 때 L개의 connection을 가진다면, DenseNet은 개의 connection이 있다(Fig. 1 참조).
이 말은 k 번째 feature map은 L-k 개의 layer들에 전달된다는 것이다.
이러한 특성때문에 이 논문을 Dense Convolutional Network(DenseNet)이라 명명했다.
Feed-forward 특성을 보존하기 위해, 각각의 layer는 additional input을 가진다.
ResNet과는 달리 더하는 것이 아닌 concatenating을 통해 결합한다.
중복되는 feature-map을 재학습할 필요가 없어 parameter가 오히려 더 적은 것은 직관과 반대되는 효과이다.
- 전통적 feed-forward 구조는 state를 가진 알고리즘으로 볼 수 있다.
Layer를 지나며 state를 바꾸고 보존할 information을 전달한다. - ResNet은 identity transformation을 더함으로써 명시적으로 information을 보존한다.
- ResNet 변형 연구에서 많은 layer는 매우 적게 관여해서 randomly dropped되기도 한다.
- 또 다른 변형 연구에서는 ResNet의 state를 unrolled RNN과 유사하게 만들었지만, 각 layer가 parameter가 너무 많아 훨씬 커졌다.
DenseNet은 추가된 정보와 보존할 정보를 명시적으로 구분한다.
DenseNet layer는 매우 좁아서(한 layer 당 12 filter) 오직 적은 수의 feature-map set만 network의 "collective knowledge"에 더하고 나머지 feature-map은 그대로 둔다.
(filter concatenate할 때 "기존 + 새로운 filter 수"가 될텐데 새로운 filter 수가 적어서(narrow,12 per layer) "기존 + 12"가 되니까 큰 변화가 없다는 듯?)
그리고 마지막 classifier는 모든 feature-map에 기반하여 결정을 내린다.
Parameter 효율성 말고도 큰 이점이 있다.
바로 information과 gradient flow의 개선이 되었고, 학습이 쉬워졌다.
또 각 layer가 loss function의 gradient와 input에 직접 접근할 수 있어서 유사 deep supervision이 가능했고 역시 deep한 구조 학습이 쉬워졌다.
또 dense connection은 규제 효과도 있어서 small training set에 대해 overfitting이 감소했다.
DenseNet을 CIFAR-10, CIFAR-100, SVHN, ImageNet에 테스트했고, SOTA보다 더 뛰어난 결과를 얻었다.
DenseNet은 현존하는 알고리즘보다 더 적은 parameter에 더 높은 accuracy를 얻어냈다.
2. Related Work
여태 다양한 연구들을 통해 deep CNN이 발전해왔다.
- Highway Network는 100개가 넘는 layer를 bypassing path(gating units)을 사용해 성공적으로 학습했다.
- ResNet은 identity mapping을 bypassing path로 사용했다.
- 1202-layer ResNet에서는 Stochastic Depth을 사용해 성공적으로 학습했다.
Stochastic Depth란 확률적으로 layer를 drop하는 것이다.
이는
1) 모든 layer가 꼭 필요한 것은 아니다
2) deep network에서 많은 중복이 있다
라는 사실을 시사한다.
DenseNet 논문은 이러한 관측에서 출발했다. - Pre-activation ResNet 또한 1000개가 넘는 layer로 SOTA를 달성했다.
- Deeper한 network를 만드는 orthogonal(깊다에 수직적 의미로 넓히다를 쓴 듯)한 방법인 width 넓히기도 있다.
대표적인 예로 GoogLeNet(Inception module), wide generalized resdiaul block을 사용한 ResNet이 있다. 사실 ResNet은 깊이만 충분하다면 filter 수 늘리기만 해도 성능이 증가한다. - FractalNet 또한 wide network structre로 좋은 성과를 냈다.
- DenseNet은 feature reuse로 parameter를 줄이고 train을 쉽게 했다.
Feature-map을 concatenate하는 것은 subsequent layer의 input에 variation을 늘리고, 효율성을 높인다.
Concatenate하는 구조인 Inception Network와 비교해서 DenseNet이 더 간단하고 효율적이다. - 좋은 성과를 낸, 주목할만한 network 구조들이 있다.
대표적으로
1) Network in Network(NIN, layer안에 micro multi-layer 삽입)
2) Deep Supervised Network(DSN, 내부 layer가 auxiliary classifier에 연결되어 earlier layer의 gradient를 강화)
3) Ladder Network(autoencoder로 연결해 semi-supervised로 accuracy 증가)
4) Deep-Fused Nets(DFNs, intermediate layer를 different base network와 연결해 information flow 개선)
5) Reconstruction loss를 최소화하기 위해 network를 pathway로 증가시키는 형태
가 있다.
3. DenseNets
Convolutional network를 지나가는 single image 를 생각해보자.
이다.
은 BN, ReLU, Poolinig, Conv와 같은 operation들이 적용된 non-linear transformation이다.
은 l번째 layer의 output이다.
ResNets
전통적인 convolutional feed-forward network는 l번째 layer와 (l+1)번째 layer를 connect하고,
여기에 ResNet은 skip-connection까지 추가했다.
ResNet의 이점은 gradient가 identity function을 통해 layer간 직접 흐를 수 있다는 것이다.
그러나 이 계산은 덧셈이라 network에서 information flow를 지연시킬 수 있다.
Dense connectivity
Information flow를 개선하기 위해 새로운 연결법을 제시한다.
한 layer를 그 후에 나오는 모든 layer와 연결하는 것이다.
여기서 는 0, .. l-1 layer의 feature-map을 single tensor로 concatenate한 것이다.
Composite function
타 논문에 영감받아, 을 BN, ReLU, 3x3 conv의 합성함수로 정의했다.
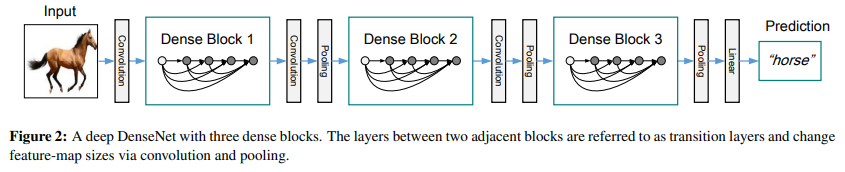
Pooling layers
앞서 나온 feature-map은 size가 변해서 viable하지 않다.
그래서 down-sampling과 size change를 위해 dense bock에 뒤이어 transition layer를 넣었다.
이는 BN, 1x1 conv 그리고 2x2 average pooling layer로 구성된다.
Growth rate
각각의 이 k개의 feature-map을 만든다면, l번째 layer는 input으로 개의 feature map을 가질 것이다(는 처음 input channel 수).
DenseNet은 k=12 정도의 좁은 layer로 구성되어 있지만, small growth rate로도 충분히 SOTA급 성능을 낼 수 있었다.
아마도 이는 feature-map들이 쌓이고 쌓여 network의 "collective knowledge"를 만들고, 이는 global state처럼 보이기 때문이다.
또 일단 한 번 쓰이면, network 어디에서든 접근 가능하기에 replicate할 필요가 없다.
Bottleneck layers
각 layer의 output이 오직 k개의 feature-map이어도, input은 더 많다.
그래서 3x3 conv 이전에 input feature-map 수를 줄이기 위해 1x1 conv를 넣는데, 이를 bottleneck layer라 했다.
Input feature-map이 감소함에 따라 컴퓨팅 효율성도 증가했다.
DenseNet에 효과적인 bottleneck layer를 적용한 발견했는데, 이를 적용한 버전을 DenseNet-B라 하기로 했다.
실험에서 1x1 convolution이 4k개의 feature-map을 만들도록 했다.
Compression
모델 경량화를 위해, transition layer에서 feature-map 수를 줄일 수 있었다.
만일 dense block이 m개의 feature-map을 만든다면, transition layer가 개의 output feature-map을 만들도록 했다.
여기서 이며, 이면 feature-map 수는 변하지 않는다.
인 경우를 DenseNet-C라 했고, 만일 앞서 디자인한 bottleneck과 transition layer가 같이 쓰였다면 DenseNet-BC라 했다.
Implementation Details
ImageNet을 제외한 나머지 dataset에서는 아래의 구조를 사용했다.
- 3개의 dense block을 가지며 각각의 layer수는 같다.
- 첫 dense block 이전에, 16 output channel(DenseNet-BC의 경우 2k)을 가진 convolution을 적용했다.
- 3x3 kernel size의 conv에 대해서는 1 pixel로 zero padding해서 feature-map size가 고정되게 했다.
- 1x1 conv - 2x2 average pooling 을 dense block 사이에 사용했다.
- 마지막 dense block 뒤에는 global average pooling을 한 후 softmax classifier를 적용했다.
- 세 dense block의 feature-map 크기는 32x32, 16x16, 8x8이다.
- 기본 DenseNet은 {L=40, k=12}, {L=100, k=12}, {L=100, k=24}로 실험했고,
DenseNet-BC에 대해서는 {L=100, k=12}, {L=250, k=24}, {L=190, k=40}으로 실험했다.
ImageNet에 대해서는 아래와 같다.
- DenseNet-BC를 사용했다.
- 224x224 input image에 대해 dense block을 4개 사용했다.
- 첫 conv layer는 2k 개의 7x7 conv(stride 2)로 구성된다.
- 다른 feature-map 수는 k를 따른다.
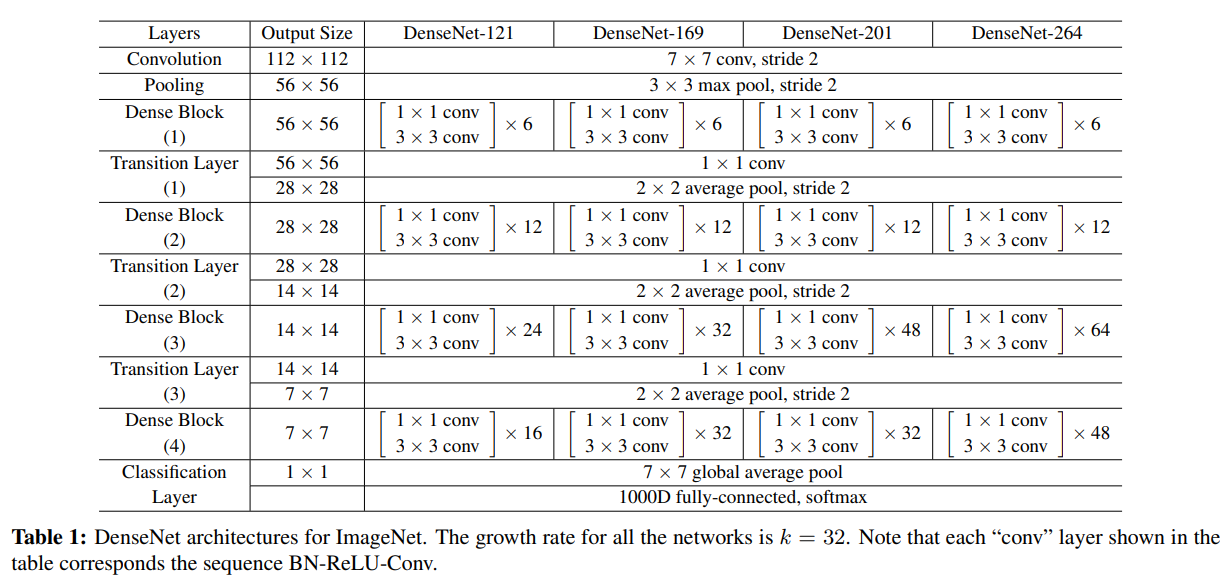
자세한 detail은 아래의 Table 1을 참조하자.
자세한 구조는 Table 1을 참조하자.
Table 1: ImageNet에 사용한 DenseNet이다. k=32이며 각 conv layer는 BN-ReLU-Conv의 순서를 따르고 있다.
4. Experiments
DenseNet의 효율성을 benchmark dataset을 써서 평가하고, SOTA(특히 ResNet) 구조와 비교할 것이다.
4.1 Datasets
CIFAR
CIFAR-10은 10개의 class, CIFAR-100은 100개의 class로 구성된 32x32 pixel의 image set이다.
Training과 test set은 각각 50,000, 10,000개의 image가 있고, 5,000개의 training image는 validation set으로 활용했다.
Data augmentation은 널리 사용되는 전략(mirroring/shifting)을 사용했고 적용된 data는 +를 붙여 표기했다(ex. C10+ = CIFAR-10 with data augmentation).
전처리는 평균과 표준편차로 정규화했고, 50,000개의 training 이미지를 모두 사용해 하긋ㅂ한 후 최종 test error를 report했다.
SVHN
SVHN(Street View House Numbers)는 32x32 크기의 colored digit images이다.
73,257개의 training image, 26,032개의 test image가 있고, 추가적 학습을 위한 531,131개의 image도 있다.
모든 training data를 활용했고 어떠한 data augmentation도 적용하지 않았다.
Validation set은 training set에서 분리한 6,000개의 image이다.
학습 중 가장 낮은 validation error를 보여준 model을 선택했고 그 model의 test error를 report했다.
전처리는 타 논문을 따라했고, pixel값을 255로 나눠 [0,1] 범위에 있도록 했다.
ImageNet
ILSVRC 2012 classification dataset인 ImageNet은 1000개의 class, 120만개의 training image, 50,000개의 test image로 구성되어 있다.
타 논문과 같은 data augmentation을 적용했고, 224x224로 signle-crop이나 10-crop을 적용했다.
Validation set에서의 classification error를 report했다.
4.2 Training
공통점
- 각 학습은 SGD로 이뤄졌다.
- 의 weight decay와 momentum이 0.9인 Nesterov(dampening x)를 사용했다.
- 가중치는 He initialization을 적용했다.
CIFAR과 SVHN에서는 아래와 같이 적용했다.
*Batch size는 64이고 각각 300/40 epoch 동안 학습했다.
- 초기 learning rate는 0.1이며, training epoch의 50%, 75%에 도달할 때마다 10으로 나눴다.
- Data augmentation이 없는 dataset에 대해서는 dropout을 각 conv(첫 conv 빼고!) 뒤에 더했다. Dropout rate는 0.2이다.
- Test error는 오직 한 번만 측정했다.
ImageNet에서는 아래와 같이 적용했다.
- Batch size는 256이고 90 epoch 동안 학습했다.
- 초기 learning rate는 0.1이며, epoch 30과 60에서 10으로 나눴다.
초기 DenseNet은 memory 효율성이 좋지 않아, GPU에서 원활한 학습을 위해 memory-efficient DenseNet을 만들었다(자세한 것은 technical report를 참고하자).
Technical Report : https://arxiv.org/pdf/1707.06990.pdf
4.3 Classification Results on CIFAR and SVHN
DenseNet을 다른 k, L로 학습했다.
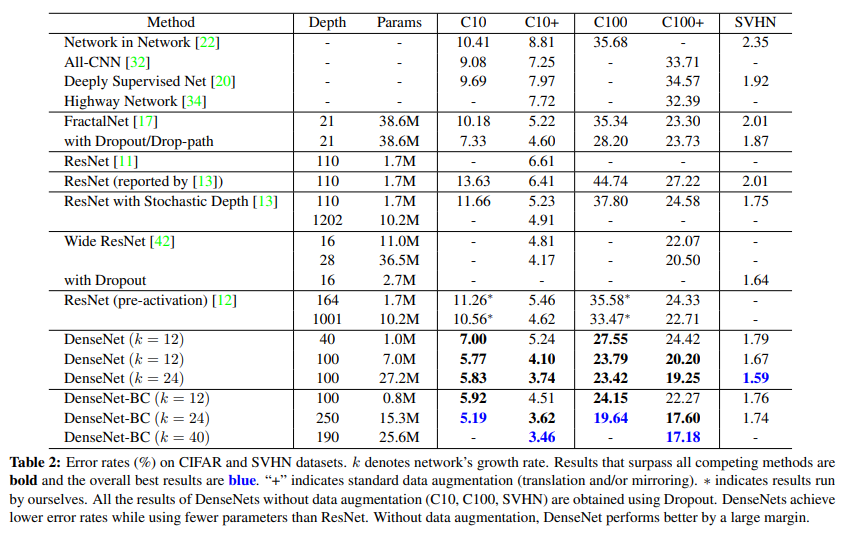
결과는 Table 2.에 잇다.
Bold로 쓰여진 내용은 SOTA를 뛰어넘은 결과이며, Blue는 그 중 최고의 결과이다.
Accuracy
Table 2의 맨 아래 열을 보면 DenseNet-BC가 L=190, k=40에서 모든 CIFAR dataset에 대해 SOTA를 뛰어넘는 결과를 보여준다.
C10+에서는 error rate 3.46%, C100+에서는 17.18%로 기존의 wide ResNet으로 나온 것보다 훨씬 낮은 수치이다.
C10과 C100에서 얻은 최고의 결과는 심지어 더 낫다.
둘 다 drop-path regularization을 쓴 FractalNet보다 30% 가량 낮다.
SVHN에서, DenseNet(L=100, k=24)은 또한 wide ResNet으로 얻어진 최고의 기록을 뛰어넘는다.
그러나 250-layer DenseNet-BC는 더 shorter layer model보다 성능이 좋지 않은데,
이는 아마 SVHN이 비교적 쉬운 과제이자, training set에 overfitting되었을 수 있기 때문이다.
Capacity
Compression이나 bottleneck layer가 없을때는, DenseNet은 L과 k가 증가할수록 성능이 좋아지는 경향이 있다.
이는 C10+과 C100+에서 두드러지게 나타난다.
L과 k가 커질수록 error가 drop하는 것을 볼 수 있다.
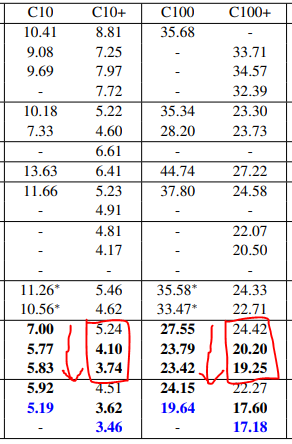
이는 DenseNet이 크고 깊은 model의 representational power를 잘 이용하고, overfitting에서 자유로운 것으로 보인다.
Parameter Efficiency
Table 2의 결과는 DenseNet이 parameter를 다른 구조(특히 ResNet)보다 더 효율적으로 사용함을 보여준다.
DenseNet-BC(bottleneck, dimension reduction)은 특히 parameter를 효율적으로 사용한다.
DenseNet-BC 250-layer model은 15.3M parameter를 가지고 있는데,
그럼에도 30M보다 많은 parameter를 가진 Fractalnet이나 WideResNet보다 성능이 좋다.
또 1001-layer pre-activaton ResNet과 DenseNet-BC(L=100, k=12)를 비교해보면, 90% 더 적은 parameter에도 비슷한 성능을 보여준다.
1001-layer pre-activation ResNet vs DenseNet-BC
- C10+에서 4.62% vs 4.51%
- C100+에서 22.71% vs 22.27%
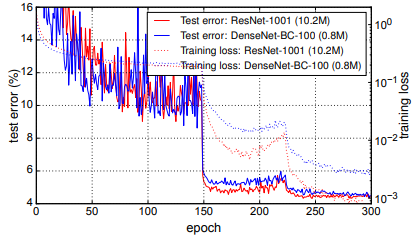
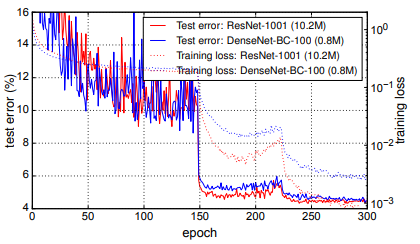
Fig. 4는 C10+에서 두 network의 training loss와 test error를 보여준다.
1001-layer deep ResNet은 더 낮은 training loss에 수렴하지만 test error는 비슷하다.
이는 아래에서 더 자세하게 분석할 것이다.
(아마도 training loss가 낮아진다 -> fitting이 된다
그러나 test error가 비슷하다 -> 실제 성능이 비슷하다
즉 ResNet은 더 많이 fitting해야 성능이 비슷해지지만, DenseNet은 더 적은 학습으로도 성능이 비슷하다는 것)
Overfitting
DenseNet이 parameter를 효율적으로 쓰는 것의 또다른 장점은 overfitting할 가능성이 낮다는 것이다.
Data augmentation이 없는 dataset에서 그 진가가 드러났다.
- C10에서, error는 기존의 7.33%에서 5.19%로 약 29% 감소했다.
- C100에서, error는 기존의 28.20%에서 19.64%로 약 30% 감소했다.
이 실험에서, k=12에서 14로 바꿈으로써 parameter를 4배 키운 결과, error는 5.77%에서 5.83%로 증가했다.
DenseNet-BC는 bottleneck과 compression layer 덕에 이러한 현상에 잘 대응했다.
4.4 Classification Results on ImageNet
DenseNet-BC를 다른 깊이와 growth rate로 ImageNet에 대해 평가했고, 이를 SOTA ResNet 구조와 비교했다.
공정한 비교를 위해, 오직 model만 바꾸고 나머지는 그대로 두었다
(ex. data-preprocessing, optimization, 이는 ResNet을 Torch로 구현해서 해결함)
그냥 단순히 ResNet을 DenseNet-BC로 바꾸기만 하고 나머지는 모두 ResNet과 동일하게 사용했다.
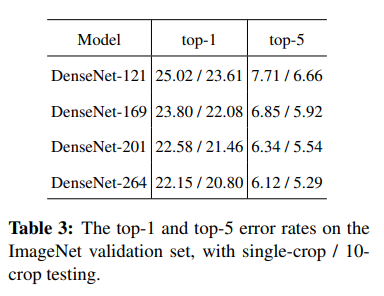
ImageNet에서 DenseNet의 single-crop, 10-crop validation error를 Table 3에 나타냈다.
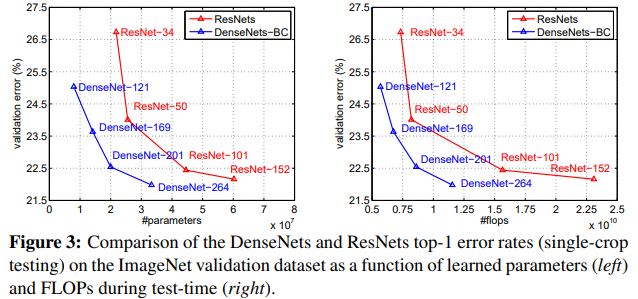
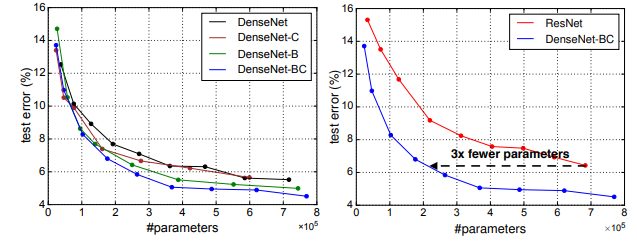
Figure 3는 single-crop의 top1 validation error를 ResNet과 DenseNet에서 비교한다.
각각 parameter 수와 FLOPs의 함수로 표현했다.
결과는 DenseNet이 SOTA ResNet보다 더 적은 parameter, 더 적은 컴퓨팅으로 더 훌륭한 성능을 보여주었다.
이러한 실험은 ResNet에 최적화된 hyperparameter 세팅으로 했기에 더 발전의 여지가 있다.
5. Discussion
DenseNet은 사실 ResNet과 거의 비슷하다.
다른 점이라면 의 input이 sum 대신 concatenate라는 것이다.
(물론 논문에는 안 나와있지만 sum을 concatenate으로 바꾼 것 말고도 layer의 feature-map이 all subsequent layer로 전달되는 것도 다른 점이다)
그러나 이러한 작은 차이가 큰 변화를 일으켰다.
Model compactness
DenseNet이 layer의 feature-map을 all subsequent layer로 전달하여 reuse를 하는 것은 곧 compact model로 이어졌다.
Figure 4의 좌측 두 그래프는 DenseNet의 변형과 ResNet을 parameter 수에 따른 test error를 나타낸다.
C10+에서 다양한 깊이로 학습했다.
DenseNet-BC는 가장 parameter 효율적인 구조이다.
비슷한 수준의 accuracy를 위해 ResNet의 1/3 정도인 parameter만 있어도 충분했다.
또 0.8M의 trainable parameter를 가진 DenseNet-BC는 10.2M parameter를 가진 1001-layer pre-activation ResNet과 성능이 비슷했다.
(0.8M vs 10.2M.. 10배 차이가 넘는다)
(근데 위에서는 1/3인데 왜 여기서는 10배 차이인가 하면
위의 그래프는 parameter가 0.7M vs 0.2M이고, 아래는 10.8M vs 0.8M이다.
Error rate을 조금 낮출 때마다 엄청난 parameter 상승이 동반되고, ResNet이 훨씬 가파르게 상승해서 이와 같은 차이가 벌어진 것 같다.)
Implicit Deep Supervision
Dense Convolutional Network의 뛰어난 성능에 대한 또다른 해석은,
아마 layer가 shorter connection을 통과한 loss function으로부터 추가적인 supervision(추가 정보를 받음)이 이뤄져서 그렇다고 생각할 수 있다.
즉 DenseNet을 일종의 "deep supervision"으로 생각할 수 있다.
(Deep supervision의 장점은 DSN 논문에 잘 나와있다.)
DenseNet은 내부적으로 유사 deep supervision을 수행한다
: network 말단의 하나의 classifier가 최대 2~3개의 transiton layer를 통해 모든 layer에 대한 direct supervision을 제공한다.
그럼에도 loss function과 gradient는 같은 loss function을 공유하기에 비교적 덜 복잡하다.
Stochastic vs deterministic connection
Dense convolutional 구조와 stochastic depth regularization은 약간의 관계가 있다.
Stochastic depth에서, residual network의 layer는 randomly dropped된다.
Pooling layer는 절대 drop되지 않기에, network가 DenseNet과 유사한 패턴을 보여준다.
확률상, pooling layer 사이의 모든 layer가 drop되어 direct 연결이 될 수 있다.
(direct 연결의 효과를 시사하는듯)
두 방법이 완전 다르지만 stochastic depth regularization에 대한 DenseNet 관점의 해석은 insight를 제공해준다.
Feature Reuse
디자인에 따르면, DenseNet은 이전 layer들의 feature-map에 layer가 접근하게 해준다(물론 transition layer를 지나치는 경우도 있지만).
처음에 DenseNet을 C10+에 L=40, k=12로 훈련시켰다.
각 layer l에 대해, layer s의 연결에 대한 average weight를 계산해 heat-map으로 나타냈다.
(l, s)가 red dot이라는 의미는 layer l이 이전에 생긴 layer s의 feature-map을 강하게 사용한다는 뜻이다.
(연관이 높다는 뜻)
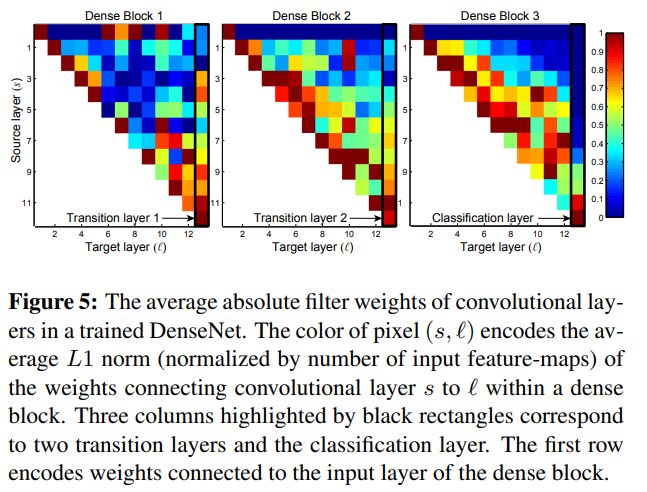
Fig. 5
(s, l)은 layer s에서 l을 잇는 weight의 average L1 norm을 나타낸 것이다
검은 사각형은 각각 2개의 transition layer, classification layer이다.
여기서 몇 가지 특성을 볼 수 있다.
- 모든 layer는 같은 block 내에서 input들에게 weight를 퍼뜨린다(색이 얼추 고르다 = 모두 연관이 있다)
이 말은 매우 초기의 layer의 feature도 동일한 dense block의 deep layer에서 직접 쓰인다는 것이다.
- 모든 layer는 같은 block 내에서 input들에게 weight를 퍼뜨린다(색이 얼추 고르다 = 모두 연관이 있다)
- Transition layer의 weight 또한 이전의 dense block layer들에게 weight를 퍼뜨린다
(target layer = Transition(세로줄)일 때 색이 얼추 고르게 퍼져있다 = indirect(Transition을 거치면 변환이 되므로 직접적 방식은 아니다)한 방법으로도 information이 이동한다).
즉 information이 몇 개의 간접적 방식으로 first to last layer로 이동한다.
- Transition layer의 weight 또한 이전의 dense block layer들에게 weight를 퍼뜨린다
- 두번째와 세번째 dense block은 transition layer에게 최소한의 weight만 할당한다
(색이 푸른색에 가깝다 = weight가 작다).
즉 transition output이 상당한 중복이 있고 DenseNet-BC에서 compress되는 결과와 일치한다(compress해도 좋은 결과 = 중복이 있어 중요도를 낮춰도 괜찮다).
- 두번째와 세번째 dense block은 transition layer에게 최소한의 weight만 할당한다
- 마지막 classification layer도 전체 dense block에 weight를 쓰긴 하지만,
마지막 feature-map에 집중된 것으로 보아 high-level feature은 나중에 생김을 알 수 있다
(붉은색이 아래에 집중됨 = 마지막 feature-map들의 중요도가 높음 = high-level feature가 나중에 생김).
- 마지막 classification layer도 전체 dense block에 weight를 쓰긴 하지만,
6. Conclusion
DenseNet은 direct connection을 통해 성능 발전을 이뤘다.
Dense구조는 또한 overfitting을 방지해주며, 더 적은 parameter와 컴퓨팅 비용으로 SOTA 성능을 보여줬다.
Feature reuse는 redundancy를 줄여 model을 compact하게 해줬다.
Code
구현
BottleNeck
class BottleNeck(nn.Module):
def __init__(self, in_channels, growth_rate):
super(BottleNeck, self).__init__()
inner_channels = 4 * growth_rate
self.residual = nn.Sequential(
# BN - ReLU - 1x1 - BN - ReLU - 3x3
# 1x1 conv = make before feature-map to 4k, if layers go deep, it become big, so downsize
nn.BatchNorm2d(in_channels),
nn.ReLU(),
nn.Conv2d(in_channels, inner_channels, kernel_size = 1, stride = 1, padding = 0, bias = False),
# 3x3 conv
nn.BatchNorm2d(inner_channels),
nn.ReLU(),
nn.Conv2d(inner_channels, growth_rate, kernel_size = 3, stride = 1, padding = "same", bias = False)
)
self.shortcut = nn.Sequential()
def forward(self, x):
return torch.cat([self.shortcut(x), self.residual(x)], dim=1)먼저 bottleneck 구조를 구현한다.
BottleNeck(for imagenet) 구조는 BN - ReLU - 1x1 - BN - ReLU - 3x3 이고
1x1는 channels을 무조건 4k(growth rate)로 만들고, 3x3은 k개의 feature map을 만드는 것을 기억하자.
결과는 이전까지의 input feature map + 현재 k개의 feature map을 해주면 된다.
Transition
class Transition(nn.Module):
def __init__(self, in_channels, out_channels):
super(Transition, self).__init__()
self.BN = nn.BatchNorm2d(in_channels)
self.relu = nn.ReLU()
self.conv = nn.Conv2d(in_channels, out_channels, kernel_size = 1, stride = 1, padding = 0, bias=False)
self.avgpool = nn.AvgPool2d(kernel_size = 2, stride = 2)
def forward(self, x):
x = self.BN(x)
x = self.relu(x)
x = self.conv(x)
x = self.avgpool(x)
return xTransition이다.
1x1 conv + 2x2 avg pooling이다.
Table 1을 보면 each "conv" layer는 BN-ReLU-Conv 구조이므로 저렇게 추가했다.
Transition은 channel을 바꿔주므로 input, output channel수가 필요하다.
DenseNet
class DenseNet(nn.Module):
def __init__(self, nblocks, growth_rate=12, reduction=0.5, num_classes=10, init_weight = True):
super(DenseNet, self).__init__()
self.growth_rate = growth_rate
# initial convolution layer comprises 2k convolutions - paper
inner_channels = 2 * growth_rate
self.conv1 = nn.Sequential(
nn.Conv2d(3, inner_channels, kernel_size = 7, stride= 2, padding = 3),
nn.MaxPool2d(kernel_size = 3, stride = 2)
)
# now channels = 2k
# Dense Block 1
layers = []
for i in range(nblocks[0]):
layers.append(BottleNeck(inner_channels, self.growth_rate))
# every time concatenate, +k
inner_channels += self.growth_rate
self.dense1 = nn.Sequential(*layers)
# Transition 1
out_channels = int(reduction * inner_channels)
self.trans1 = Transition(inner_channels, out_channels)
inner_channels = out_channels
# Dense Blcock 2
layers = []
for i in range(nblocks[1]):
layers.append(BottleNeck(inner_channels, self.growth_rate))
# every time concatenate, +k
inner_channels += self.growth_rate
self.dense2 = nn.Sequential(*layers)
# Transition 2
out_channels = int(reduction * inner_channels)
self.trans2 = Transition(inner_channels, out_channels)
inner_channels = out_channels
# Dense Blcock 3
layers = []
for i in range(nblocks[2]):
layers.append(BottleNeck(inner_channels, self.growth_rate))
# every time concatenate, +k
inner_channels += self.growth_rate
self.dense3 = nn.Sequential(*layers)
# Transition 3
out_channels = int(reduction * inner_channels)
self.trans3 = Transition(inner_channels, out_channels)
inner_channels = out_channels
# Dense Blcock 4
layers = []
for i in range(nblocks[3]):
layers.append(BottleNeck(inner_channels, self.growth_rate))
# every time concatenate, +k
inner_channels += self.growth_rate
self.dense4 = nn.Sequential(*layers)
# Classifier
self.bn = nn.BatchNorm2d(inner_channels)
self.relu = nn.ReLU()
self.avgpool = nn.AdaptiveAvgPool2d((1,1))
self.linear = nn.Linear(inner_channels, num_classes)
if init_weight:
self._initialize_weights()
def forward(self, x):
x = self.conv1(x)
x = self.dense1(x)
x = self.trans1(x)
x = self.dense2(x)
x = self.trans2(x)
x = self.dense3(x)
x = self.trans3(x)
x = self.dense4(x)
x = self.bn(x)
x = self.relu(x)
x = self.avgpool(x)
x = nn.Flatten()(x)
x = self.linear(x)
return x
# initialize weights
def _initialize_weights(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
if m.bias is not None:
# if bias exist, bias = 0
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.BatchNorm2d):
nn.init.constant_(m.weight, 1)
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.Linear):
nn.init.normal_(m.weight, 0, 0.01)
nn.init.constant_(m.bias, 0)전체 구조이다.
조금 노가다를 한 감이 없지 않지만.. 그래도 한 눈에 보여서 이렇게 했다.
먼저 처음 input conv인 7x7은 channel을 2k로 바꾼다.
따라서 Conv2d(3, 2k)로 했다. 참고로 3은 3x224x224의 3이다.
그 다음 DenseBlock 파트이다.
nblocks(i)로 각 DenseBlock(i)의 개수를 받아 for문으로 처리했다.
layers라는 list에 넣고 nn.Sequential에 unpack했다.
여기서 중요한 점은 inner_channels에 self.growth_rate를 더해주는 것이다.
그 이유는 앞서 BottleNeck 하나 당 k channel의 feature map이 concatenate된다.
따라서 이전 channel + k이므로 해줘야 한다.
Transition 파트는 쉽다.
Out_channels를 reduction rate와 inner_channel을 곱한 값으로 정한다.
그리고 Transition block을 지정한 후, 이 channel이 다음 block의 inner channel이 될 것 이므로 inner_channels = out_channels로 지정한다.
마지막에 Average Pooling을 1x1 size로 해주고
Linear layer를 통과시켜 Classification layer도 구현한다.
다만 마지막 classifier에서 average pooling과 linear는 이해가 되지만 왜 BN/ReLU를 해주는지 모르겠다.
아마 Dense block에서 conv로 끝나서 BN-ReLU를 추가해준 것 같은데.. 일단 논문상에는 없다.
참고한 코드들이 모두 사용해서 쓰긴 했다.
Result
일단 사이즈가 엄청 줄었다.
ResNet50의 경우..
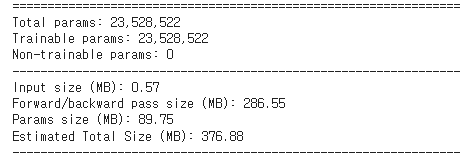
DenseNet121의 경우..
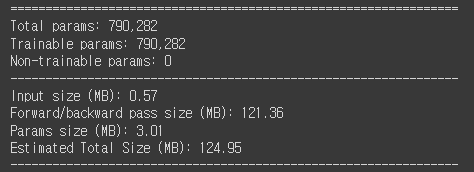
Layer는 DenseNet이 약 2배가량 많지만 parameter는 거의 30배 줄고 Total size도 1/3로 줄었다!
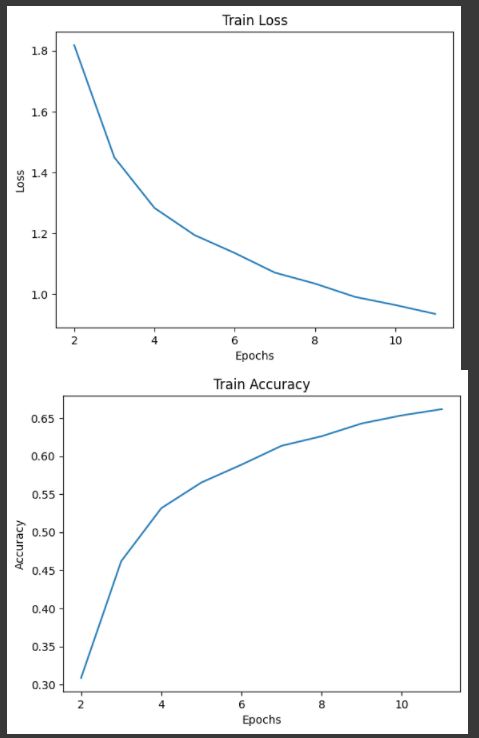
학습 결과는 아래와 같다.
원래라면 Dense-BC 121이 아니라 논문에서 CIFAR용 구조를 따로 줬지만..
Dense-BC가 복잡하지만 훨씬 효율적이라 구현해보고 싶었다(bottleneck, compression).
물론 참고한 코드들이 DenseNet 121을 쓰기도 함 ^^.
여튼 CIFAR-10을 학습하기엔 충분하다고 생각된다.
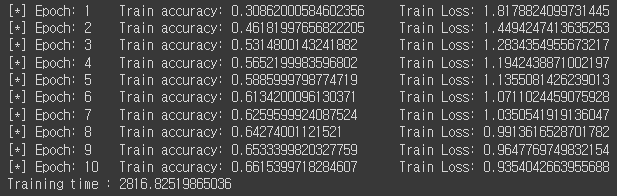
Hyperparameter setting(lr=0.1, batch=64, epoch=10)을 따로 하지 않아서 accuracy가 천천히 증가했는데,
epoch를 늘리고 hyperparameter 조정하면 더 좋아질 듯 하다.
모델이 작아서 학습이 빠르다 ^^.
전체 코드는 github에 있습니다~~.
https://github.com/Parkyosep/Papers/tree/main/DenseNet
Appendix - Optimizer
최적화 방법에 SGD, Nesterov, Momentum without dampening이라 되어있어
아니 대체 Nesterov로 한다는거야, SGD로 한다는거야 하고 찾아봤는데..
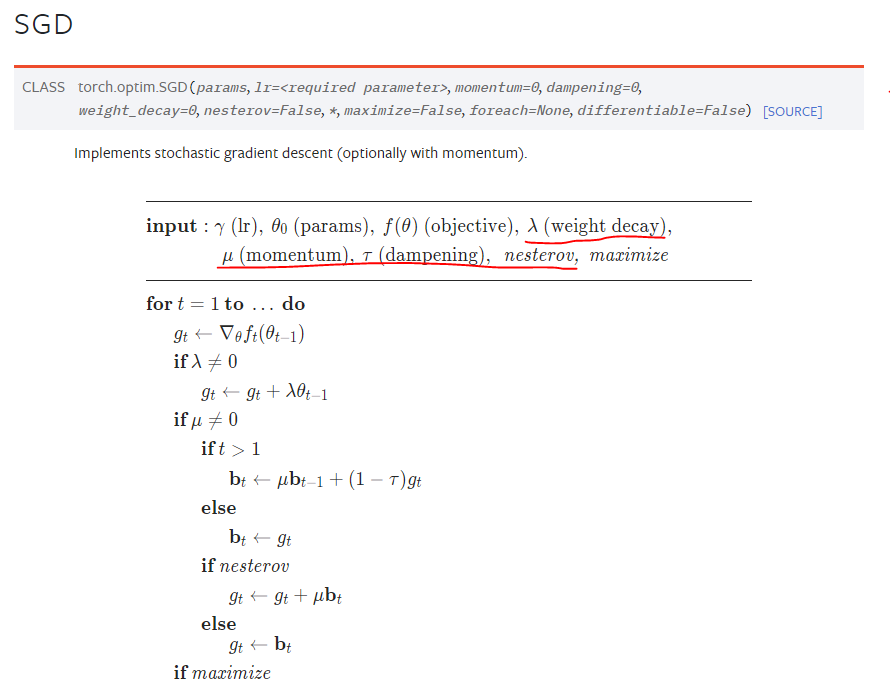
사실 Nesterov가 SGD 기반이라.. 그렇게 한다는 거였다.
설명이 SGD하고 ~중간에 다른 설명~ 하고 Nesterov라 대체 뭘 쓴다는거지..? 했는데
같은거였다니.. 부끄럽다.
PyTorch는 위에서 torch.optim.SGD(params, momentum=0.9, nesterov=True로 하면 된다.
예전에 공부했었는데.. 기본 지식의 소실에 따른 실수..
추후 Optimizer도 복습해야겠다.
Reference
Paper
[1] https://deep-learning-study.tistory.com/528
[2] https://sike6054.github.io/blog/paper/sixth-post/
Code
[3] https://deep-learning-study.tistory.com/545
[4] https://github.com/andreasveit/densenet-pytorch/blob/master/densenet.py