주성분 분석이란
고차원의 데이터를 저차원의 데이터로 환원시키는 기법이다.
여기서 '차원'은 변수의 개수를 의미하므로, 많은 변수를 최대한 정보의 손실 없이 압축하여 그 개수를 줄이는 알고리즘이라고 이해하면 된다.
데이터를 압축하지 않더라도, 기본적으로 데이터의 특성이 가장 잘 보이는 방향으로 변수를 바꿔주기 때문에 데이터 분석에 많이 활용된다.
주성분 분석을 사용하는 이유
데이터의 차원이 커질수록 분석을 위해 필요한 데이터 개수가 기하급수적으로 증가하게 된다. 이러한 현상을 '차원의 저주'라 하는데, 차원이 증가하면서 학습 데이터 수가 차원의 수보다 적어져 성능이 저하되거나, 데이터 개수가 충분하다고 하더라도 학습에 많은 시간과 비용이 소모된다는 점에서 데이터의 차원이 커지는 것을 방지할 필요가 있다.
주성분 분석의 원리
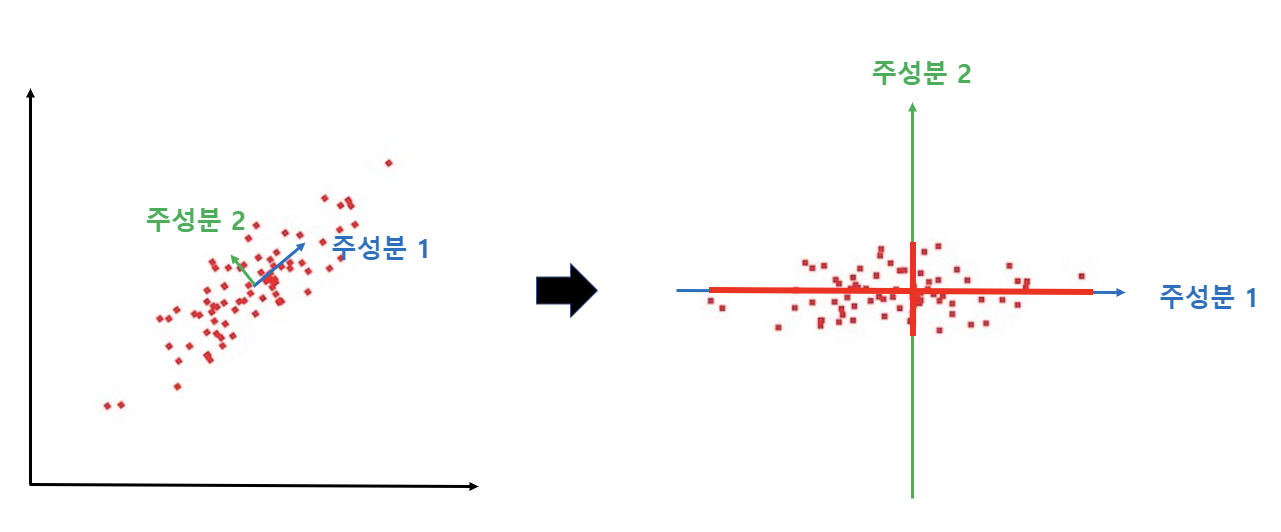
주성분 분석은 데이터의 분산이 가장 크게 나타나는 방향을 찾아, 새로운 변수로 뽑아낸다. 위 그림에서, 데이터를 왼쪽처럼 관찰하는 것보다, 오른쪽처럼 축을 잡아 관찰하는 것이 데이터의 정보를 더 효과적으로 볼 수 있을 것이다.
주성분 분석의 수학적 이해
독립변수 X를 표준화한 결과를 Z라고 하면, 주성분 분석으로 뽑아낸 변수 P는 다음과 같이 표현된다.
따라서 주성분 분석을 위한 우리의 목표는 좌표 변환 행렬 A를 구하는 것이라 볼 수 있다.
주성분 축(P)은 데이터의 분산이 큰 순서대로 생성되므로, 우리는 P의 분산이 최대가 되는 경우의 A를 찾으면 된다. 다만 분산이 무한히 커지는 것을 막기위해, ‖A‖ = 1 이라는 제약조건 안에서 A를 찾게 된다. P는 표준화된 데이터이므로, 자기자신의 제곱을 이용해 분산을 구할 수 있다.
P의 분산을 나타내면 아래와 같다.
이제 라그랑주 승수법을 이용해서 분산 Vp가 최대일 때 A를 구해보자
🔸라그랑주 승수법이란?
최댓값이나 최솟값을 찾고 싶은 함수 f(x,y)와 제한조건 g(x,y)=c가 있을 때, 제한조건을 만족시키는 함수 f의 최댓값이나 최솟값을 편미분을 이용해 구하는 방법으로, 사용되는 라그랑주 함수는 아래와 같다.
라그랑주 함수 L을 x와 y에 대해 편미분하면 총 2개의 식을 얻을 수 있으며, 여기에 제약 조건인 g(x,y)=c를 이용하면 미지수가 3개인 문제의 해를 구할 수 있다. 여기에서 구한 x와 y는 제약 조건 g를 만족하는 함수 f의 최적점이 될 가능성이 있는 점이다.
라그랑주 승수법을 현재 우리의 상황에 적용해보자.
위 내용을 바탕으로 분산 Vp에 대한 라그랑주 함수를 구하면 아래와 같다.
위 식을 A로 편미분해보자.
결국 위 식을 통해 분산 Vp가 최대가 되는 좌표변환행렬 A를 구할 수 있다. 위 식을 푸는 과정은 상관행렬 R의 고유벡터와 고윳값을 구하는 과정과 동일하다.
(R - λI)의 행렬식이 0이라는 식을 풀면 고윳값 λ를 구할 수 있고, λ를 이용해 A를 구할 수 있다.
고윳값(eigen value)과 고유벡터(eigen vector)
임의의 행렬 K가 (nxn)인 정방행렬일 때, 아래 식을 만족하는 0이 아닌 벡터 v와 정수 λ가 존재한다면, λ를 행렬 K의 고윳값이라 하고, v를 행렬 K의 고유벡터라 한다.
위 식을 정리해보면 아래와 같다.
λ가 정수이므로, I를 곱해서 행렬로 변환한다.
양변에 (K-λI)의 역행렬을 곱한다.
이와 같이 (K-λI)의 역행렬이 존재할 경우, 벡터 v가 0이 되므로 (K-λI)는 역행렬이 존재하지 않아야 한다.
위 방정식을 풀면 행렬의 고윳값과 고유벡터를 구할 수 있다.
주성분 분석 순서
개념적 순서
- 데이터 표준화
- 주성분 축 생성
2-1. 첫번째 축 생성
◾ 데이터의 분산이 가장 큰(데이터가 가장 넓게 펴져있는) 방향을 구한다.
◾ 그 뱡향으로 첫번째 축을 만든다.
2-2. 두번째 축 생성
◾ 첫번째 축과 90도로 직교하며, 분산이 두번째로 큰 방향을 구한다.
◾ 그 뱡향으로 두번째 축을 만든다.
2-3. 세번째 축 생성
... - 구한 새로운 공간으로 원래의 데이터 좌표를 이동
수학적 순서
- 데이터 표준화
- 표준화된 데이터(Z)의 상관행렬(R) 구하기
- 상관행렬(R)의 고윳값(λ), 고유벡터(A)를 구하기
- 고유벡터(A)를 이용해서 표준화된 데이터(Z)를 주성분 공간으로 이동
출처- "데이터 분석을 떠받치는 수학"(손민규 지음)
scikit-learn을 사용하여 파이썬에서 주성분 분석 구현
샘플 데이터 준비
# 필요한 라이브러리 추가
import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
from matplotlib import font_manager, rc
import numpy as np
# 샘플 데이터 불러오기
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
df = pd.read_csv(url, names=['sepal length','sepal width','petal length','petal width','target'])
df.head()독립변수 표준화
# 독립변수들만 추출
x = df.drop(['target'], axis=1).values
# 종속변수 추출
y = df['target'].values
# 표준화 (array 형태로 반환)
std_x = StandardScaler().fit_transform(x)
features = ['sepal length', 'sepal width', 'petal length', 'petal width']
x_df = pd.DataFrame(std_x, columns=features)
x_df주성분 추출
pca = PCA(n_components=4) # 주성분 개수 결정
printcipalComponents = pca.fit_transform(std_x)
principalDf = pd.DataFrame(data=printcipalComponents, columns = ['PC1', 'PC2', 'PC3', 'PC4'])
principalDf기여율과 누적기여율 확인
# 한글깨짐방지
font_path = "malgun.ttf"
font = font_manager.FontProperties(fname=font_path).get_name()
rc('font', family=font)
# 그래프 그리는 함수
def explained_variance_ratio_plot(explained_variance_ratio):
x_axis = range(1, len(explained_variance_ratio)+1)
plt.bar(x_axis, explained_variance_ratio,
align = 'center')
plt.step(x_axis, np.cumsum(explained_variance_ratio),
where = 'mid', color='red')
plt.ylim(0, 1.1)
plt.xticks(x_axis)
plt.xlabel('주성분')
plt.ylabel('기여율')
plt.grid()
plt.show()
explained_variance_ratio_plot(pca.explained_variance_ratio_)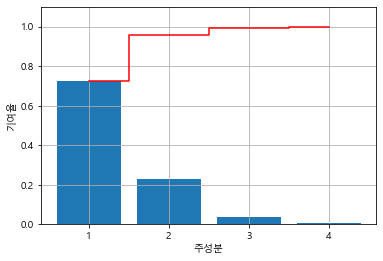
*막대그래프: (개별)기여율
*빨간선그래프: 누적기여율
고윳값과 고유벡터 확인
# 상관 행렬
R = x_df.corr(method = 'pearson')
# (w=고윳값),(v=고유벡터),(R.values=DataFrame인 R을 numpy array로 변환)
w, v = np.linalg.eig(R.values)
# 고윳값
eig_value = pd.DataFrame(w, columns=['eigenvalue'], index=['PC1', 'PC2', 'PC3', 'PC4'])
eig_value = eig_value.T # or eig_value.transpose()
eig_value# 고유벡터
eig_vectors = pd.DataFrame(v, columns=['PC1', 'PC2', 'PC3', 'PC4'], index=features)
eig_vectors주성분 분석에서 고윳값과 고유벡터의 의미
⭐ 고유벡터
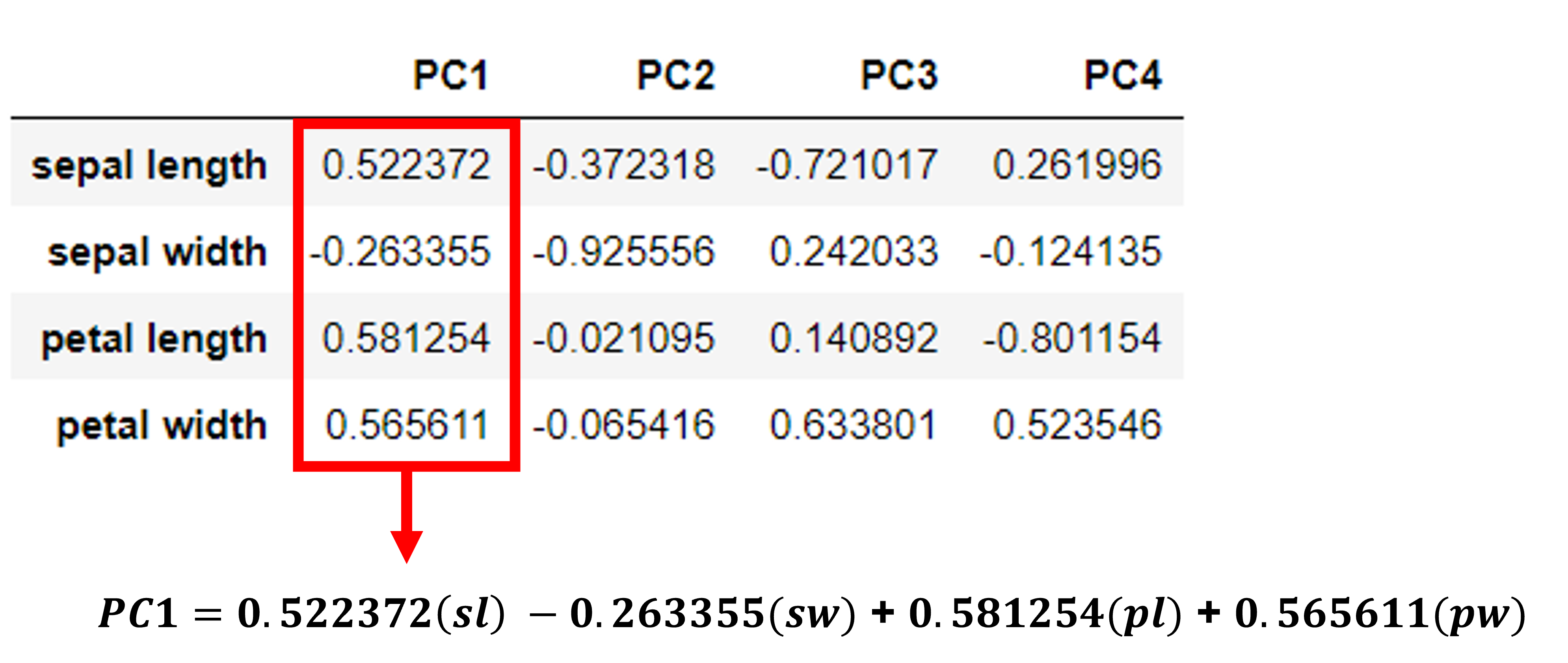
고유벡터는 주성분(P)와 표준화된 독립변수(Z) 사이의 관계를 보여준다. 예를 들어, 위와 같은 고유벡터를 통해 우리는 첫번째 주성분(PC1)이
0.522372*(sepal length) - 0.263355*(sepal width) + 0.581254*(petal length) + 0.565611*(petal width) 로 구해짐을 알 수 있다.
⭐ 고윳값
◾ 각 주성분의 분산과 고윳값은 일치한다.
따라서 고윳값을 각 주성분이 담고 있는 데이터의 정보량이라고 볼 수 있다. 표준화된 데이터는 각 축(변수)의 정보량(분산)이 1로 동일했으나, 주성분들은 각자 나타내는 정보량이 다르다.
위 사진에서 PC1의 경우, 고윳값이 2.910818 이므로, 대략 포함하는 정보량이 원래 변수의 2.9배 정도됨을 알 수 있다.
◾ 좌표변환 전과 후의 분산의 합은 같다.
좌표변환 전 분산의 합 = 1 + 1 + 1 + 1 = 4 (변수가 4개이므로)
좌표변환 후 분산의 합 = 2.910818 + 0.921221 + 0.147353 + 0.020608 = 4
데이터의 차원을 축소하는 방법
차원을 축소하는 방법을 보기 전, 먼저 기여율과 누적 기여율이 무엇인지 확인하자.
⭐ 기여율
전체 정보량 중 자기 정보량의 비율
ex) PC1의 기여율 = =
⭐ 누적 기여율
첫번째 주성분부터 자기 정보량까지 총합의 비율
ex) PC2의 누적기여율 = =
차원을 축소하는 방법에는 2가지가 있다.
-
고윳값을 이용해서 축소하는 방법
✔ 고윳값이 1보다 작은 주성분 축을 삭제
표준화된 데이터의 한 축의 정보량이 1이었으므로, 1보다 작은 정보량을 가진 주성분 축을 삭제함으로써 차원을 축소할 수 있다.
위 예제에서는 PC1을 제외한 모든 주성분 축의 고윳값이 1보다 작으므로, PC1만을 사용하고, 나머지는 모두 삭제한다고 볼 수 있다. -
누적 기여율을 이용해서 축소하는 방법
✔ 원래 데이터 정보량의 몇 %를 이용할 것인지 정해서 나머지는 삭제
예를 들어, 원래 정보량의 96%까지 사용하기로 했다면, 위 예제에서 PC1, PC2 축만 남기고 나머지를 삭제하면 된다. PC2의 누적 기여율이 0.95800975이기 때문이다.
