[데이터분석] 선형회귀분석

박서현·2021년 8월 5일

데이터분석 머신러닝 선형회귀분석

데이터분석

목록 보기

3/4

회귀분석(regression analysis)이란

두 변수 사이의 관계를 방정식으로 구하는 것. 크게 단순회귀와 다중회귀로 나뉜다. 단순회귀는 독립변수가 1개이고, 다중회귀는 독립변수가 2개 이상으로 구성된다.

회귀식

단순회귀: $y = w_0x_0 + w_1x_1$ ( $x_0$ 는 1인 상수항)
다중회귀: $y = w_0x_0 + w_1x_1 + w_2x_2 + \cdots + w_nx_n$ ( $x_0$ 는 1인 상수항)

$w_0,w_1$ 등은 회귀계수라 부르며, 종속변수(Y)에 대한 독립변수(X)의 가중치를 나타낸다. 회귀분석에서 우리의 목표는 이러한 회귀계수를 구하는 것이다.

최소제곱법(OLS)

실제값(Y)과 회귀식으로 예측한 값(y)의 차이를 '잔차(residual)'라 하는데, 이 잔차를 최소화하는 방식으로 회귀식을 구하는 방법을 '최소제곱법'이라 한다. 가능한 수많은 회귀식 중에서 잔차들의 제곱합을 최소화하는 것을 찾는 방법이다.

y = Xw

잔차를 구해보면 아래와 같다.

e = Y-y = Y-Xw

잔차의 제곱합(residual sum of squares)을 구해보자.

RSS = e^Te = (Y-Xw)^T(Y-Xw)

= Y^TY−2Y^TXw+w^TX^TXw

잔차의 제곱합이 최소가 되려면 가중치 벡터 w에 대해서 미분한 값이 0이어야 한다.

{dRSS \over dw} = −2X^TY+2X^TXw = 0

∴ X^TY = X^TXw

만약 $X^TX$ 의 역행렬이 존재한다면 가중치 벡터 w를 아래와 같이 구할 수 있다.

w = (X^TX)^{−1}X^TY

$X^TX$ 의 역행렬이 존재하고, 구한 값에서 RSS가 최소값을 가지려면, 아래의 식이 성립해야한다.

{d^2RSS \over dw^2} = 2X^TX > 0

파이썬을 이용한 최소제곱법 구현

회귀분석용 데이터 생성

# 라이브러리 추가
import numpy as np 
import pandas as pd 
import statsmodels.api as sm
from sklearn.datasets import make_regression
import matplotlib.pyplot as plt
from matplotlib import font_manager, rc
from sklearn.linear_model import LinearRegression

# 회귀분석용 가상데이터 생성
bias = 100
X0, y, w = make_regression(
    n_samples=200, n_features=1, bias=bias, noise=10, coef=True, random_state=1
)
X = sm.add_constant(X0)
y = y.reshape(len(y), 1)
w

# y = 100 + 86.44794301x + e 생성됨
>> Out[1] array(86.44794301)

1. OLS 해를 직접 이용하는 방법

w = np.linalg.inv(X.T @ X) @ X.T @ y
w

# y = 99.79150869 + 86.86.96171201x 로 회귀식 예측
>> Out[2] array([[99.79150869],
                 [86.96171201]])

$w = (X^TX)^{−1}X^TY$ 의 식을 이용하여 가중치 벡터를 직접 구했다.

# 한글깨짐방지
font_path = "malgun.ttf"
font = font_manager.FontProperties(fname=font_path).get_name()
rc('font', family=font)

x_new = np.linspace(np.min(X0), np.max(X0), 10) # X0의 최솟값부터 최댓값까지 범위에서 일정하게 10개의 포인트를 뽑는다.
X_new = sm.add_constant(x_new)  # 상수항 결합
y_new = np.dot(X_new, w) # 행렬곱 y = Xw

plt.scatter(X0, y, label="원래 데이터")
plt.plot(x_new, y_new, 'rs-', label="회귀분석 예측")
plt.xlabel("x")
plt.ylabel("y")
plt.title("선형 회귀분석의 예")
plt.legend()
plt.show()

2. scikit-learn 패키지를 사용한 선형 회귀분석

model = LinearRegression(fit_intercept=True) # fit_intercept: 모형에 상수항이 있는가 없는가를 결정하는 인수. True일 때 상수항이 있다. 디폴트는 True
model = model.fit(X0, y) # fit 메서드로 가중치 값을 추정. 상수항 결합을 자동으로 해줌
x_new = x_new.reshape(len(x_new), 1) # 행개수:len(x_new), 열개수: 1개로 변경
# predict 메서드로 새로운 입력 데이터에 대한 출력 데이터 예측
y_new = model.predict(x_new) # predict를 사용할 때는 입력으로 2차원 배열을 써야한다는 점을 주의한다.

# model.intercept_ == 추정된 상수항, model.coef_ == 추정된 가중치 벡터
print(model.intercept_, model.coef_)

# y = 99.79150869 + 86.96171201x 로 회귀식 예측
>> Out[4] [99.79150869] [[86.96171201]]

3. statsmodels 패키지를 사용한 선형 회귀분석

# dataframe 생성
df = pd.DataFrame({"x": X0[:, 0], "y": y[:, 0]})
df

dfy = df[["y"]]
dfX = sm.add_constant(df[["x"]])
model = sm.OLS(dfy, dfX) # or model = sm.OLS.from_formula("y ~ x", data=df)
result = model.fit()
print(result.summary()) # y = 99.7915 + 86.9617x 로 회귀식 예측

# y값 예측
x_new = np.linspace(np.min(X0), np.max(X0), 10)
y_new = result.predict(x_new)

# result.resid == 잔차 벡터, result.params == 추정된 가중치 벡터
print(result.params)


>> Out[6]

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.985
Model:                            OLS   Adj. R-squared:                  0.985
Method:                 Least Squares   F-statistic:                 1.278e+04
Date:                Thu, 05 Aug 2021   Prob (F-statistic):          8.17e-182
Time:                        13:07:31   Log-Likelihood:                -741.28
No. Observations:                 200   AIC:                             1487.
Df Residuals:                     198   BIC:                             1493.
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const         99.7915      0.705    141.592      0.000      98.402     101.181
x             86.9617      0.769    113.058      0.000      85.445      88.479
==============================================================================
Omnibus:                        1.418   Durbin-Watson:                   1.690
Prob(Omnibus):                  0.492   Jarque-Bera (JB):                1.059
Skew:                           0.121   Prob(JB):                        0.589
Kurtosis:                       3.262   Cond. No.                         1.16
==============================================================================

const    99.791509
x        86.961712
dtype: float64

# 잔차 벡터 시각화
result.resid.plot(style="o")
plt.title("잔차 벡터")
plt.xlabel("데이터 번호")
plt.ylabel("잔차")
plt.show()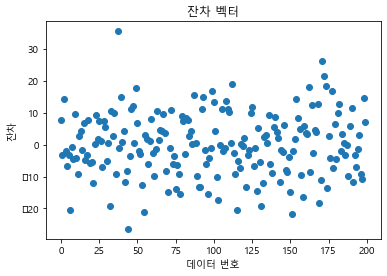

회귀식을 평가하는 방법

⭐ 평균제곱근오차(RMSE 또는 RMS, Root Mean Square Error)

RMS = \sqrt{\sum_{i=1}^{n}(y_i - Y_i)^2 \over n}

⭐ 결정계수( $R^2$ , coefficient of determination)

회귀식에 의해 실제 데이터가 어느 정도 설명되는지를 나타내는 지표이다.

SST(총변동) = \sum_{i=1}^{n}(Y_i-\bar{Y})^2

SSR(회귀변동) = \sum_{i=1}^{n}(y_i-\bar{Y})^2

SSE(잔차변동) = \sum_{i=1}^{n}(Y_i-y_i)^2

R^2 = {SSR\over SST} = {SST-SSE\over SST} = 1 - {SSE\over SST}

= {\sum_{i=1}^{n}(y_i-\bar{Y})^2 \over \sum_{i=1}^{n}(Y_i-\bar{Y})^2}

결정계수는 0에서 1 사이 값을 가지며, 1에 가까울수록 회귀식의 성능이 좋다고 볼 수 있다.

0 ≦ R^2 ≦ 1

변수가 많아질수록 결정계수가 커지는 것을 막기위해서 조정된 결정계수를 사용하기도 한다.

Adjusted\space R^2 = 1 - ({n-1\over n-m-1}\times{SSE\over SST})

n은 데이터의 개수, m은 변수의 개수를 의미한다.

다중공선성(multicollinearity)

독립변수 간에 높은 상관관계가 있는 것을 다중공산성이라고 한다. 서로 연관성이 많은 독립변수들을 사용하게되면 회귀계수의 안정성이 떨어져, 회귀식의 안정성 역시 떨어지게 된다.

다중공선성을 확인하는 방법으로는 크게 2가지가 있다.

상관행렬 확인
이전 포스트에서 개념 설명했으니 skip
분산팽창인수(VIF, variation index factor) 확인
🔸 VIF란?
변수가 n개 있을 때, 이들 중 하나를 종속변수로 두고, 나머지를 독립변수로 둔 후, 회귀식을 계산하여 상관성을 확인하는 방법이다.

VIF_k = {1 \over 1-R_k^2}

k는 종속변수로 둔 k번째 변수를 의미하고, $R_k^2$ 은 회귀식의 결정계수를 의미한다.

❗ $R_k^2$ 가 1에 가깝다 = $VIF_k$ 이 무한히 커진다 = 다중공선성 문제가 있다

일반적으로 VIF가 10 이상이면 다중공선성 문제가 있다고 판단한다.

변수들간의 다중공선성 문제를 피하기 위해, 주성분회귀(PCR) 또는 부분최소제곱(PLS) 등의 회귀 방식을 사용할 있다.

박서현

차곡차곡 쌓아가기

이전 포스트

[데이터분석] 주성분 분석

다음 포스트

[데이터분석] 선형회귀분석

데이터분석

[데이터분석] 주성분 분석

[데이터분석] 부분최소제곱법

0개의 댓글