[데이터분석] 기초 수학적 지식

박서현·2021년 8월 4일
공분산데이터표준화분산상관계수정규분포통계평균표준편차행렬확률
0

데이터분석

목록 보기
1/4

데이터 분석에 정말정말 기초가 되는 지식들이기 때문에 간략하게 정리해놓고 넘어가려 한다.

(산술)평균(average)

xˉ=1n∑i=1nxi\bar{x} = {1\over n}\sum_{i=1}^{n}x_i

모집단인 경우 평균은 μ로 나타낸다.

중앙값(median)

데이터를 크기 순으로 정렬했을 때 가운데 있는 값
데이터 개수가 홀수인 경우: n+12n+1\over 2번째 값
데이터 개수가 홀수인 경우: n2n\over 2번째 값과 n2+1{n\over 2}+1번째 값의 평균

모집단(population)

어떤 집단의 전체 데이터

표본집단(sample)

전체 데이터 중에서 추출된 부분집합

분산(variance)

데이터가 평균을 기준으로 얼마나 퍼져있는가에 대한 지표

S2=1n−1(∑i=1n(xi−xˉ)2)S^2 = {1 \over n-1}\left(\sum_{i=1}^{n}\left(x_i - \bar{x}\right)^2\right)

모집단인 경우 n-1 대신 n으로 나눈다.
모집단인 경우 분산의 기호는 σ²로 나타낸다.

표준편차(standard deviation)

S=S2=1n−1(∑i=1n(xi−xˉ)2)S = \sqrt{S^2} = \sqrt{{1 \over n-1}\left(\sum_{i=1}^{n}\left(x_i - \bar{x}\right)^2\right)}

모집단인 경우 n-1 대신 n으로 나눈다.
모집단인 경우 표준편차의 기호는 σ로 나타낸다.

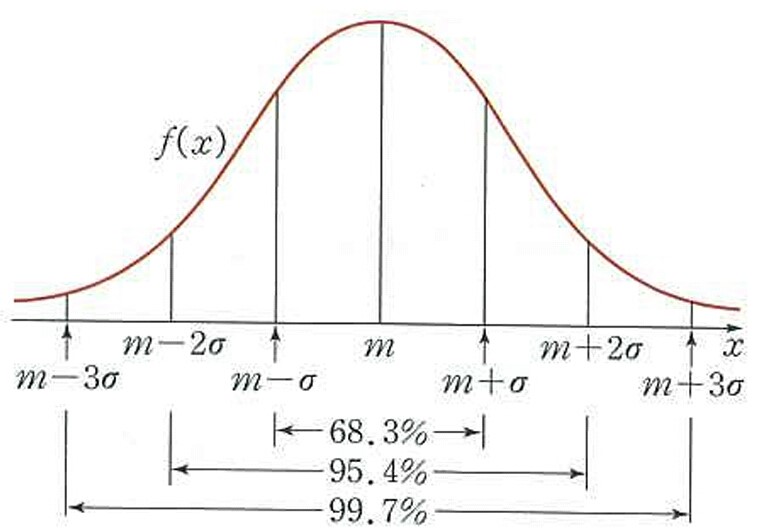
정규분포(normal distribution)

데이터의 분포가 종 모양처럼 평균을 기준으로 좌우 대칭이 되는 확률분포

데이터 표준화(data standardization)

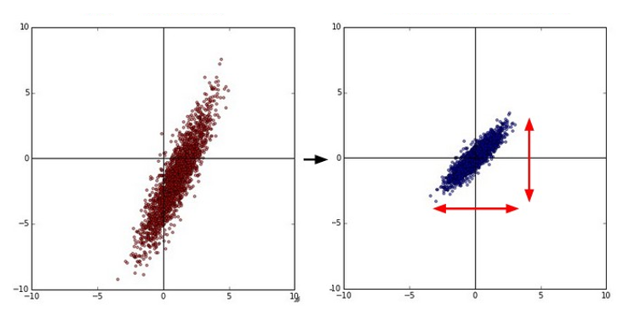
서로 다른 척도를 가진 데이터를 비교하기 위해서 데이터 표준화를 사용한다. 데이터 표준화를 거치면
1. 데이터의 단위가 사라지고,
2. 평균은 0이 되고,
3. 표준편차는 1이 된다.

zi=(xi−xˉ)σz_i = {\left(x_i - \bar{x}\right) \over σ}

데이터를 표준화하는 방법은, 데이터과 평균과의 오차를 구한 후, 이를 표준편차로 나누는 것이다. 표준화한 데이터를 Z값(Z-value, Z score)이라 한다.

공분산(covariance)

2개의 확률변수의 선형 관계를 나타내는 값이다.

Sxy=1n−1(∑i=1n(xi−xˉ)(yi−yˉ))S_{xy} = {1 \over n-1}\left(\sum_{i=1}^{n}\left(x_i - \bar{x}\right)\left(y_i - \bar{y}\right)\right)

숫자 자체보다, 부호에 의미가 있다.
부호가 +이면 X, Y 데이터가 비례 관계이고, 부호가 -이면 X, Y 데이터가 반비례 관계임을 나타낸다.

상관계수(correlation)

공분산을 통해 데이터 간의 비례 or 반비례 관계는 알 수 있지만, 그 관계가 어느 정도인지까지는 알 수 없다. 이 정도를 알려주는 것이 상관계수이다.

Rxy=SxySxSy=∑(xi−xˉ)(yi−yˉ)∑(xi−xˉ)2∑(yi−yˉ)2R_{xy} = {S_{xy}\over S_xS_y} = {\sum(x_i - \bar{x})(y_i - \bar{y}) \over \sqrt{\sum(x_i - \bar{x})^2}\sqrt{\sum(y_i - \bar{y})^2}}
−1≦Rxy≦1-1\leqq R_{xy}\leqq 1

데이터가 표준화된 경우, 상관계수는 아래와 같다.
Rxy=∑(xi−xˉ)(yi−yˉ)(n−1)SxSy=1(n−1)∑i=1n((xi−xˉ)Sx(yi−yˉ)Sy)R_{xy} = {{\sum(x_i - \bar{x})(y_i - \bar{y})\over (n-1)}\over S_xS_y} = {1 \over (n-1)}\sum_{i=1}^{n}\left({(x_i - \bar{x})\over S_x}{(y_i - \bar{y})\over S_y}\right)
=1(n−1)∑i=1nzxizyi= {1 \over (n-1)}\sum_{i=1}^{n}z_{x_i}z_{y_i}

일반적으로 상관계수가 0.6 이상이면 강한 상관관계가 있는 것으로 본다.

정방행렬(square matrix)

(nxn) 행렬

단위행렬(identity matrix)

I=[10⋯001⋯0⋮⋮1⋮00⋯1]I = \begin{bmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & 1 & \vdots \\ 0 & 0 & \cdots & 1 \\ \end{bmatrix}

대각선을 제외한 나머지 값들이 모두 0이고, 대각선의 값은 모두 1인 정방행렬

전치행렬(transpose matrix)

A=[a11a12⋯a1ma21a22⋯a2m⋮⋮aij⋮an1an2⋯anm]ATorA′=[a11a21⋯an1a12a22⋯an2⋮⋮aij⋮a1ma2m⋯amn]A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1m} \\ a_{21} & a_{22} & \cdots & a_{2m} \\ \vdots & \vdots & a_{ij} & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nm} \\ \end{bmatrix} A^T or A' = \begin{bmatrix} a_{11} & a_{21} & \cdots & a_{n1} \\ a_{12} & a_{22} & \cdots & a_{n2} \\ \vdots & \vdots & a_{ij} & \vdots \\ a_{1m} & a_{2m} & \cdots & a_{mn} \\ \end{bmatrix}

행렬의 행과 열을 바꾼 행렬

표준화된 데이터의 분산을 행렬로 표현하기

Zx=[zx1zx2⋮zxn]Z_x = \begin{bmatrix} z_{x_1} \\ z_{x_2} \\ \vdots \\ z_{x_n} \\ \end{bmatrix}
∑i=1nzxi2=zx12+zx22+⋯+zxn2=[zx1zx2⋯zxn][zx1zx2⋮zxn]=Zx′Zx\sum_{i=1}^{n}z_{x_i}^2 = z_{x_1}^2 + z_{x_2}^2 + \cdots + z_{x_n}^2 = \begin{bmatrix} z_{x_1}z_{x_2}\cdots z_{x_n} \end{bmatrix}\begin{bmatrix} z_{x_1}\\ z_{x_2}\\ \vdots \\ z_{x_n} \end{bmatrix} = Z_x'Z_x
∴Vzx=1(n−1)∑i=1nzxi2=1(n−1)Zx′Zx∴ V_{z_x} = {1 \over (n-1)}\sum_{i=1}^{n}z_{x_i}^2 = {1\over (n-1)}Z_x'Z_x

Vzx는 X의 표준화된 데이터 Z의 분산 행렬

상관행렬

R=[rx1x1rx1x1⋯rx1xnrx2x1rx2x2⋯rx2xn⋮⋮⋱⋮rxnx1rxnx2⋯rxnxn]R = \begin{bmatrix} r_{x_1x_1} & r_{x_1x_1} & \cdots & r_{x_1x_n} \\ r_{x_2x_1} & r_{x_2x_2} & \cdots & r_{x_2x_n} \\ \vdots & \vdots & \ddots & \vdots \\ r_{x_nx_1} & r_{x_nx_2} & \cdots & r_{x_nx_n} \\ \end{bmatrix}

표준화된 데이터의 경우, 상관계수는 아래와 같이 구할 수 있다.

R=1(n−1)Zx′ZxR = {1\over (n-1)}Z_x'Z_x

역행렬(inverse matrix)

AB=BA=I일때,B=A−1(B는A의역행렬)AB = BA = I 일 때, B = A^{-1} (B는 A의 역행렬)
(A−1)−1=A(A^{-1})^{-1} = A
(AB)−1=B−1A−1(AB)^{-1} = B^{-1}A^{-1}

역행렬이 존재하기 위해서는 행렬식이 0이 아니어야함

det(A)=∣a11a12a21a22∣=∣a11a22−a12a21∣≠0det(A) = \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22}\end{vmatrix} = \begin{vmatrix} a_{11}a_{22} - a_{12}a_{21}\end{vmatrix} ≠ 0
profile
박서현
차곡차곡 쌓아가기
다음 포스트

[데이터분석] 주성분 분석

0개의 댓글