파이썬-알고리즘

1. 선형검색

리스트에서 특정한 값을 찾는 알고리즘의 하나로 순차검색알고리즘, 선형검색알고리즘이라고 한다.
리스트의 인덱스 순서대로 순차적으로 값을 검색하는 것이다.

과정

1. 리스트의 첫 번째 요소를 시작으로 현재 요소를 검사하여 찾으려는 값을 비교
2. 현재 요소가 찾으려는 값과 일치하지 않으면 다음 요소로 이동하고 다시 비교
3. 검색하려는 값을 찾거나 데이터 집합의 끝까지 검색을 진행
4. 검색이 종료되면 검색 결과를 반환, 찾으려는 값이 없으면 종료 후 "값을 찾을 수 없음(-1)"을 나타내는 특별한 값을 반환

dates = [3, 2, 5, 7, 9, 1, 0, 8, 6, 4]
print(f'dates: {dates}')
print(f'dates length: {len(dates)}')

searchData = int(input('찾으려는 숫자 입력: '))
searchResultIdx = -1

n = 0
while True:
    if n == len(dates):
        searchResultIdx = -1
        break

    elif dates[n] == searchData:
        searchResultIdx = n
        break

    n += 1

print(f'searchResultIdx: {searchResultIdx}')

#출력값
dates: [3, 2, 5, 7, 9, 1, 0, 8, 6, 4]
dates length: 10
찾으려는 숫자 입력: 9
searchResultIdx: 4

• -1은 검색 결과가 없음을 나타내는 관용적인 값으로 사용

보초법

선형검색에서 보초법이란 리스트의 마지막 인덱스에 찾으려는 값을 일부러 추가(보초를 세워두어)하는 것이다.

과정

1. 검색하려는 값을 리스트의 끝에 추가(보초 값을 설정)
2. 검색 루프를 시작(대부분 while문)
3. 현재 요소(searchData)와 검색하려는 값(보초 값 n)을 비교
4. 현재 요소가 검색하려는 값과 일치하지 않으면 다음 요소로 이동하고 루프 진행
5. 검색하려는 값을 찾을 때까지 루프를 반복후 일치하면 검색을 종료하고 반환

dates = [3, 2, 5, 7, 9, 1, 0, 8, 6, 4]
print(f'dates: {dates}')
print(f'dates length: {len(dates)}')

searchData = int(input('찾으려는 숫자 입력: '))
searchResultIdx = -1

dates.append(searchData)

n = 0
while True:
    if dates[n] == searchData:
        if n != len(dates) - 1:
            searchResultIdx = n
        break

    n += 1

print(f'dates: {dates}')
print(f'dates length: {len(dates)}')
print(f'searchResultIdx: [{searchResultIdx}]')

#출력값
dates: [3, 2, 5, 7, 9, 1, 0, 8, 6, 4]
dates length: 10
찾으려는 숫자 입력: 4
dates: [3, 2, 5, 7, 9, 1, 0, 8, 6, 4, 4]
dates length: 11
searchResultIdx: [9]

실습

• 리스트에서 가장 앞에 있는 숫자 ‘7’을 검색하고 위치(인덱스)를 출력하자.

nums = [4, 7, 10, 2, 4, 7, 0, 2, 7, 3, 9]

nums = [4, 7, 10, 2, 4, 7, 0, 2, 7, 3, 9]
print(f'nums: {nums}')
print(f'nums length: {len(nums)}')

searchData = int(input('input search number: '))
searchResultIdx = -1

nums.append(searchData)

n = 0
while True:
    if nums[n] == searchData:
        if n != len(nums) - 1:
            searchResultIdx = n
        break
    n += 1

print(f'nums: {nums}')
print(f'nums length: {len(nums)}')
print(f'searchResultIdx: {searchResultIdx}')

if searchResultIdx < 0:
    print('not search index')
else:
    print(f'search index: {searchResultIdx}')
    
#출력값
nums: [4, 7, 10, 2, 4, 7, 0, 2, 7, 3, 9]
nums length: 11
input search number: 7
nums: [4, 7, 10, 2, 4, 7, 0, 2, 7, 3, 9, 7]
nums length: 12
searchResultIdx: 1
search index: 1

• 리스트에서 숫자 ‘7’을 모두 검색하고 각각의 위치(인덱스)와 검색 개수를 출력하자.
  nums = [4, 7, 10, 2, 4, 7, 0, 2, 7, 3, 9]

nums = [4, 7, 10, 2, 4, 7, 0, 2, 7, 3, 9]
print(f'nums: {nums}')
print(f'nums length: {len(nums)}')

searchData = int(input('input search number: '))
searchResultIdxs = []

nums.append(searchData)

n = 0
while True:
    if nums[n] == searchData:
        if n != len(nums) - 1:
            searchResultIdxs.append(n)
        else:
            break

    n += 1

print(f'nums: {nums}')
print(f'nums length: {len(nums)}')
print(f'searchResultIdxs: {searchResultIdxs}')
print(f'searchResultCnts: {len(searchResultIdxs)}')

#출력값
nums: [4, 7, 10, 2, 4, 7, 0, 2, 7, 3, 9]
nums length: 11
input search number: 7
nums: [4, 7, 10, 2, 4, 7, 0, 2, 7, 3, 9, 7]
nums length: 12
searchResultIdxs: [1, 5, 8]
searchResultCnts: 3

2. 이진검색

리스트가 정렬이 되어있다는 전제(안됬다면 정렬을 시켜줘야 함)에 오름차순으로 정렬된 리스트에서 특정한 값의 위치를 찾는 알고리즘이다.

과정

1. 먼저 중앙값을 찾는다.
2. 중앙값과 찾고자 하는 값을 비교한다.
3. 찾으려는 값이 중앙값과 같다면 탐색 종료후 인덱스 반환
   중앙값보다 작다면 검색범위를 중앙값의 오른쪽 부분으로 설정
   중앙값보다 크다면 검색범위를 중앙값의 왼쪽 부분으로 설정
4. 이런 과정을 원하는 항목을 찾거나 검색 범위가 더 이상 줄어들지 않을 때까지 반복함

datas = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]

print(f'datas: {datas}')
print(f'datas length: {len(datas)}')

searchData = int(input('searchData: '))
searchResultIdx = -1

staIdx = 0
endIdx = len(datas) - 1
midIdx = (staIdx + endIdx) // 2
midVal = datas[midIdx]
print(f'midIdx: {midIdx}')
print(f'midVal: {midVal}')

while searchData <= datas[len(datas)-1] and searchData >= datas[0]:

    if searchData == datas[len(datas)-1]:
        searchResultIdx = len(datas) - 1
        break
    
    elif searchData > midVal:
        staIdx = midIdx
        midIdx = (staIdx + endIdx) // 2
        midVal = datas[midIdx]
        print(f'midIdx: {midIdx}')
        print(f'midVal: {midVal}')

    elif searchData < midVal:
        endIdx = midIdx
        midIdx = (staIdx + endIdx) // 2
        midVal = datas[midIdx]
        print(f'midIdx: {midIdx}')
        print(f'midVal: {midVal}')

    elif searchData == midVal:
        searchResultIdx = midIdx
        break

print(f'searchResultIdx: {searchResultIdx}')

#출력값
datas: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
datas length: 11
searchData: 2
midIdx: 5
midVal: 6
midIdx: 2
midVal: 3
midIdx: 1
midVal: 2
searchResultIdx: 1

실습

• 리스트를 오름차순으로 정렬한 후 ‘7’을 검색하고 위치(인덱스)를 출력하자
  nums = [4, 10, 22, 5, 0, 17, 7, 11, 9, 61, 88]

먼저 정렬을 시키기 위해 sort함수(기본 오름차순) 을 이용함

datas = [ 4, 10, 22, 5, 0, 17, 7, 11, 9, 61, 88]
datas.sort()
print('datas:{}'.format(datas))
searchNum = int(input('찾으려는 값을 입력하세요:'))

searchResultIdx = -1

startIdx = 0
endIdx = len(datas) - 1
midIdx = (startIdx+endIdx) // 2
midVal = datas[midIdx]

while searchNum <= datas[len(datas)-1] and searchNum >= datas[0]:

    if searchNum == datas[len(datas) - 1]:
        searchResultIdx = len(datas) -1
        break
    elif searchNum > midVal:
        startIdx = midIdx
        midIdx = (startIdx+endIdx) // 2
        midVal = datas[midIdx]
    elif searchNum < midVal:
        endIdx = midIdx
        midIdx = (startIdx + endIdx) // 2
        midVal = datas[midIdx]
    elif searchNum == midVal:
        searchResultIdx = midIdx
        break

print('searchResultIdx:{}'.format(searchResultIdx))
#실행결과 
datas:[0, 4, 5, 7, 9, 10, 11, 17, 22, 61, 88]
찾으려는 값을 입력하세요:9
searchResultIdx:4

3. 순위 알고리즘

순위를 정하는 알고리즘으로 어떤 값과 다른 값을 비교했을때 비교한 값의 크기가 더 작다면 그 인덱스에 1을 더하는 방식으로 전체값을 하나씩 모두 비교한다.

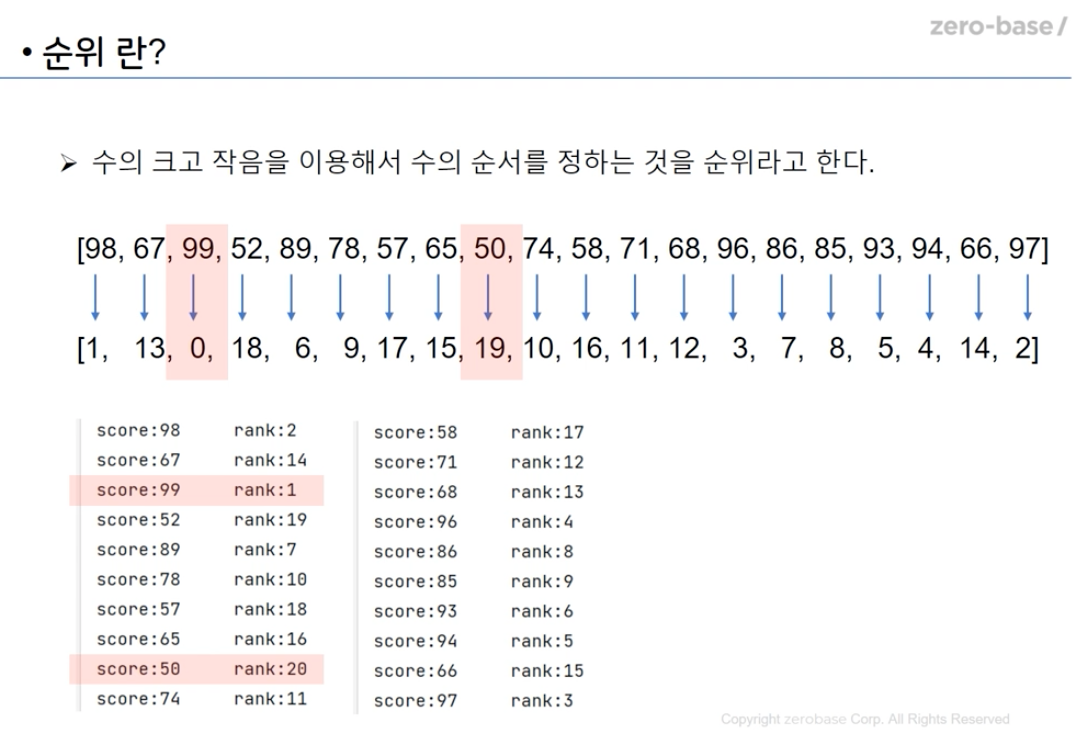
위 사진에서 98과 67을 비교해보면 98 > 67 이기때문에 67의 인덱스에 1을 더하고 다음 99를 비교하면 98 < 99 이기 때문에 98의 인덱스에 1을 더한다. 이런 과정을 반복 하면 여러 숫자들의 크고작음을 통해 각각의 값의 인덱스에 1이 여러번 더해진 것을 볼 수 있다.

import random

nums = random.sample(range(50, 101), 20)
ranks = [0 for i in range(20)] #길이가 20이고 아이템의 값이 0으로 초기화 되는 리스트 [0,0,0...]

print(f'nums: {nums}')
print(f'ranks : {ranks}')

for idx, num1 in enumerate(nums):
    for num2 in nums:
        if num1 < num2:
            ranks[idx] += 1

print(f'nums: {nums}')
print(f'ranks : {ranks}')

for i, m in enumerate(nums):     #보기 편하게 정렬시키는 방법
    print(f'nums: {m} \t rank: {ranks[i] + 1}')

#출력값
nums: [75, 91, 86, 57, 81, 54, 72, 73, 61, 89, 93, 92, 60, 51, 94, 52, 90, 99, 97, 83]
ranks : [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
nums: [75, 91, 86, 57, 81, 54, 72, 73, 61, 89, 93, 92, 60, 51, 94, 52, 90, 99, 97, 83]
ranks : [11, 5, 8, 16, 10, 17, 13, 12, 14, 7, 3, 4, 15, 19, 2, 18, 6, 0, 1, 9]
nums: 75 	 rank: 12
nums: 91 	 rank: 6
nums: 86 	 rank: 9
nums: 57 	 rank: 17
nums: 81 	 rank: 11
nums: 54 	 rank: 18
nums: 72 	 rank: 14
nums: 73 	 rank: 13
nums: 61 	 rank: 15
nums: 89 	 rank: 8
nums: 93 	 rank: 4
nums: 92 	 rank: 5
nums: 60 	 rank: 16
nums: 51 	 rank: 20
nums: 94 	 rank: 3
nums: 52 	 rank: 19
nums: 90 	 rank: 7
nums: 99 	 rank: 1
nums: 97 	 rank: 2
nums: 83 	 rank: 10

실습

모듈

class RankDeviation:

    def __init__(self,mss,ess):
        self.midStuSco = mss
        self.endStuSco = ess
        self.midRanks = [0 for i in range(len(mss))]
        self.endRanks = [0 for i in range(len(mss))]
        self.rankDeviation = [0 for i in range(len(mss))]

    def setRank(self,ss,rs):
            for idx, sco1 in enumerate(ss):
                for sco2 in ss:
                    if sco1 < sco2:
                        rs[idx] +=1

    def setMidRank(self):
        self.setRank(self.midStuSco, self.midRanks)

    def getMidRank(self):
        return  self.midRanks

    def setEndRank(self):
        self.setRank(self.endStuSco, self.endRanks)

    def getEndRank(self):
        return self.endRanks

    def printRankDeviation(self):
        for idx, mRank in enumerate(self.midRanks):
            deviation = mRank - self.endRanks[idx]
            if deviation >0:
                deviation = '↑' +str(abs(deviation))
            elif deviation <0:
                deviation = '↓' + str(abs(deviation))
            else:
                deviation = '=' + str(abs(deviation))

            print(f'midRank : {mRank} \t endRank : {self.endRanks[idx]} \t deviation : {deviation}')

실행

import book as rk
import random

midStuSco = random.sample(range(50,101),20)
endStuSco = random.sample(range(50,101),20)

rd = rk.RankDeviation(midStuSco,endStuSco)
rd.setMidRank()
print(f'midStuScors : {midStuSco}')
print(f'midRank : {rd.getMidRank()}')

rd.setEndRank()
print(f'EndStuScors : {endStuSco}')
print(f'endRank : {rd.getEndRank()}')

rd.printRankDeviation()

4. 버블 정렬

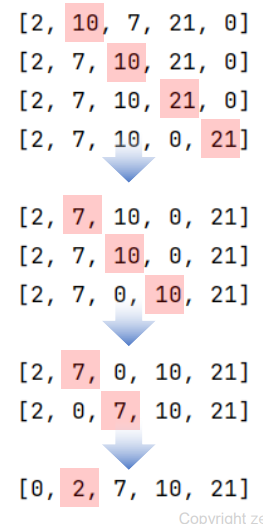
처음부터 끝까지 인접하는 인덱스의 값을 순차적으로 비교하면서 큰 숫자를 가장 끝으로 옮기는 알고리즘이다.

과정

1. 첫 번째 아이템부터 시작하여 인접한 두 아잍템을 비교
2. 두 아이템의 순서가 잘못되어 있다면(보통 큰 아이템이 작은 아이템보다 앞에 있는 경우), 두 원소의 위치를 바꿈
3. 이 과정을 반복하면 가장 큰 아이템이 리스트의 맨 끝으로 이동함
4. 두 번째 아이템도 끝에서 하나씩 줄여가며 같은 과정을 반복
5. 이러한 과정을 모든 원소가 정렬될 때까지 반복

nums = [10, 2, 7, 21, 0]
print(f'not sorted nums: {nums}')

length = len(nums) - 1

for i in range(length):
    for j in range(length - i):
        if nums[j] > nums[j+1]:
            nums[j],nums[j+1] = nums[j+1],nums[j] #자리 바꾸는 방법

        print(f'순위 변화 과정: {nums}')
print(f'sorted nums: {nums}')

#실행결과 
not sorted nums: [10, 2, 7, 21, 0]
순위 변화 과정: [2, 10, 7, 21, 0]
순위 변화 과정: [2, 7, 10, 21, 0]
순위 변화 과정: [2, 7, 10, 21, 0]
순위 변화 과정: [2, 7, 10, 0, 21]
순위 변화 과정: [2, 7, 10, 0, 21]
순위 변화 과정: [2, 7, 10, 0, 21]
순위 변화 과정: [2, 7, 0, 10, 21]
순위 변화 과정: [2, 7, 0, 10, 21]
순위 변화 과정: [2, 0, 7, 10, 21]
순위 변화 과정: [0, 2, 7, 10, 21]
sorted nums: [0, 2, 7, 10, 21]

실습

def bubbleSort(ns):
    length = len(ns) - 1
    for i in range(length):
        for j in range(length - i):
            if ns[j] > ns[j + 1]:
                ns[j], ns[j + 1] = ns[j + 1], ns[j]

    return ns

모듈

import random as rd
import bubble as bb

students = []

for i in range(20):
    students.append(rd.randint(170,185))

print(f'students : {students}')

sortedStudents = bb.bubbleSort(students)

print(f'sortedStudents : {sortedStudents}')

5. 삽입 정렬

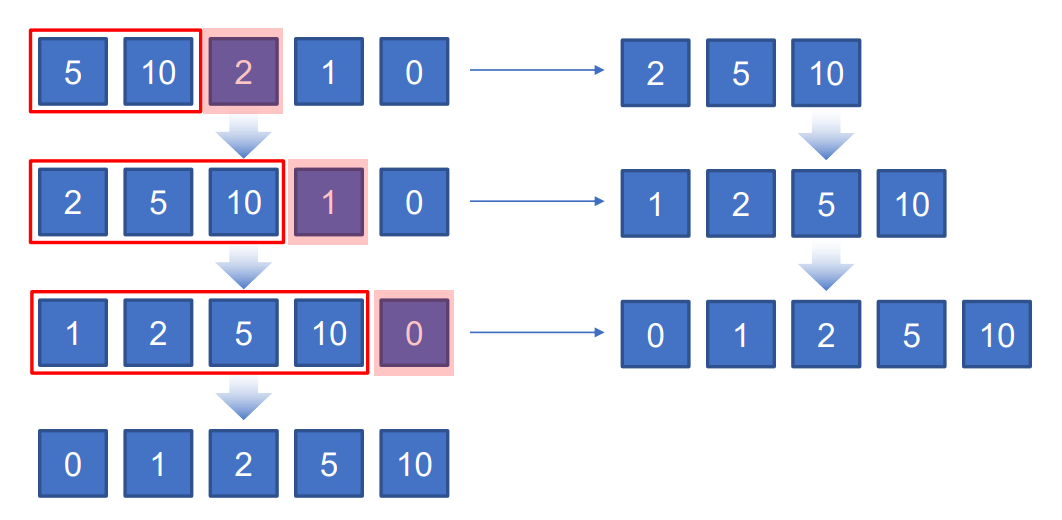
정렬되어 있는 자료배열의 아이템들과 선택한 아이템을 비교해 적절한 위치에 각 아이템을 삽입하여 정렬하는 방식
(정렬되지 않은 부분의 원소를 하나씩 선택하여 이미 정렬된 부분의 적절한 위치에 삽입하는 것)

#오름차순
nums = [5, 10, 2, 1, 0]

for i1 in range(1, len(nums)):
    i2 = i1 - 1
    cNum = nums[i1]

    while nums[i2] > cNum and i2 >= 0:
        nums[i2 + 1] = nums[i2]
        i2 -= 1

    nums[i2 + 1] = cNum

print(f'nums: {nums}')

#출력값
nums: [0, 1, 2, 5, 10]

#내림차순
nums = [5, 10, 2, 1, 0]
for i1 in range(1,len(nums)):
    i2 = i1 -1
    cNum = nums[i1]

    while nums[i2] < cNum and i2 >= 0:
        nums[i2 + 1] = nums[i2]
        i2 -=1

    nums[i2 + 1] = cNum
    print(nums)
print(f'nums : {nums}')

실습

모듈

class SortNumbers:

    def __init__(self, ns, asc = True):
        self.nums = ns
        self.isAsc = asc

    def isAscending (self, flag):
        self.isAsc = flag

    def setSort(self):

        for i1 in range(1, len(self.nums)):
            i2 = i1 =1
            cNum = self.nums[i1]

            if self.isAsc:
                while self.nums[i2] > cNum and i2 >=0:
                    self.nums[i2 + 1 ] = self.nums[i2]
                    i2 -=1
            else:
                while self.nums[i2] < cNum and i2 >=0:
                    self.nums[i2 + 1 ] = self.nums[i2]
                    i2 -= 1

            self.nums[i2 +1] = cNum

    def getSortedNumbers(self):
        return self.nums

    def getMinNumber(self):
        if self.isAsc:
            return self.nums[0]
        else:
            return self.nums[len(self.nums) -1]

    def getMaxNumber(self):
        if self.isAsc:
            return self.nums[len(self.nums) - 1]
        else:
            return self.nums[0]

실행

import random
import bank as sm

nums = random.sample(range(1,1000),100)
print(f'not sorted numbers : {nums}')
# 객체 생성
sn = sm.SortNumbers(nums)
# 오름차순
sn.setSort()
sortedNumbers = sn.getSortedNumbers()
print(f'sortedNumbers : {sortedNumbers}')

#내림차순
sn.setSort()
sortedNumbers = sn.getSortedNumbers()
print(f'sortedNumbers by DESC : {sortedNumbers}')

# min & max
print(f'min : {sn.getMinNumber()}')
print(f'max : {sn.getMaxNumber()}')

6. 선택 정렬

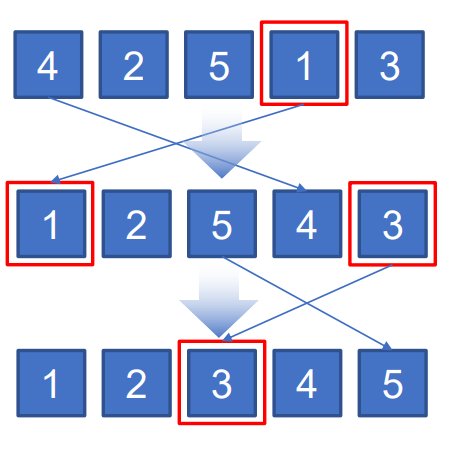
주어진 리스트에서 최소값을 찾아서 첫 번째 위치로 옮기고, 그 다음으로 작은 원소를 찾아서 두 번째 위치로 옮기는 과정을 반복하여 리스트를 정렬

nums = [4, 2, 5, 1, 3]

for i in range(len(nums)-1):
    minIdx = i
    for j in range(i+1,len(nums)): # i 다음에 있는 인덱스부터 리스트의 끝까지
        if nums[minIdx] > nums[j]:
            minIdx = j

    tempIdx = nums[i]
    nums[i] = nums[minIdx]
    nums[minIdx] = tempIdx

print(nums)
#실행결과 
[1, 2, 3, 4, 5]

i: 현재위치의 원소
j: 위치의 원소와 비교 대상이 되는 원소

실습

• 학생 20명의 시험점수를 오름차순과 내림차순으로 정렬하는 모듈을 만들어보자.

  모듈

def sortNumbers(nums,asc=True):

    if asc:
        for i in range(len(nums)-1):
            minIdx = i

            for j in range(i+1,len(nums)):
                if nums[minIdx] > nums[j]:
                    minIdx = j

            nums[i], nums[minIdx] = nums[minIdx], nums[i]
    else:
        for i in range(len(nums)-1):
            minIdx = i
            for j in range(i+1,len(nums)):
                if nums[minIdx] < nums[j]:
                    minIdx = j
            nums[i], nums[minIdx] = nums[minIdx], nums[i]

    return nums

실행

import random
import module as md

scores = random.sample(range(50,101),20)
print(scores)
print(len(scores))

result = md.sortNumbers(scores)
print(result)
#실행결과 
[59, 50, 74, 62, 58, 94, 97, 65, 80, 69, 63, 82, 78, 52, 53, 73, 96, 77, 60, 68]
20
[50, 52, 53, 58, 59, 60, 62, 63, 65, 68, 69, 73, 74, 77, 78, 80, 82, 94, 96, 97]

• 주의해야할 것은 정렬을 할 때 기존의 데이터값을 '얕은 복사'하게 되면 기존 원 데이터도 함께 정렬이 된다는 것.

즉, 위의 예제 에서 정렬된 result = md.sortNumbers(scores)의 값과 정렬하기 전의 값 print(scores) 은 같아지게된다. 이는 scores이 모듈부의 nums로 넘어갈때 주소값을 그대로 넘겨주면서 scores과 nums는 변수모양만 다를뿐 하나의 주소값을 갖게 되므로 얕은 복사가 일어나기 때문이다.

이를 방지하려면 copy함수를 이용하여 scores을 모듈에 넘겨주기전에 한번 '깊은복사'를 하여 copy한 것을 nums에 넘겨주면 해결된다.

• 깊은 복사를 하여 해결한 코드

import random
import module as md
import copy

scores = random.sample(range(50,101),20)
print(scores)
print(len(scores))

result = md.sortNumbers(copy.deepcopy(scores))
print(result)
print(scores)

7. 최댓값

가장 큰 값을 찾는 알고리즘

class MaxAlgorithm:
    def __init__(self, ns):
        self.nums = ns
        self.maxNum = 0

    def getMaxNum(self):
        self.maxNum = self.nums[0]

        for n in self.nums:
            if self.maxNum < n:
                self.maxNum = n

        return self.maxNum

ma = MaxAlgorithm([-2, -4, 5, 7, 10, 0, 8, 20])
maxNum = ma.getMaxNum()
print(f'maxNum : {maxNum}')

실습

• 리스트에서 아스키코드가 가장 큰 값을 찾는 알고리즘을 만들어보자

class MaxAlgorithm:

    def __init__(self,cs):
        self.chars = cs
        self.maxChar = 0

    def getMaxChar(self):
        self.maxChar = self.chars[0]

        for a in self.chars:
            if ord(self.maxChar) < ord(a):
                self.maxChar = a
        return self.maxChar

chars = ['c','x','Q','A','e','P','p']
ma = MaxAlgorithm(chars)
result = ma.getMaxChar()
print('아스키 코드 값이 가장 큰 값은:{}'.format(result))
#실행값 
아스키 코드 값이 가장 큰 값은:x

8. 최솟값

가장 작은 값을 찾는 알고리즘

class MinAlgorithm:
    #초기화 하는 역할
    def __init__(self, ns):
        self.nums = ns
        self.minNum = 0

    def getMinNum(self):
        self.minNum = self.nums[0]

        for n in self.nums:
            if self.minNum > n:
                self.minNum = n

        return self.minNum

nums = [-2, -4, 5, 7, 10, 0, 22]
ma = MinAlgorithm(nums)
minNum = ma.getMinNum()
print(f'minNum : {minNum}')

실습

• 리스트에서 아스키코드가 가장 작은값을 찾는 알고리즘을 만들어보자

class MinAlgorithm:
    #초기화 하는 역할
    def __init__(self, cs):
        self.chars = cs
        self.minChar = 0

    def getMinChar(self):
        self.minChar = self.chars[0]

        for c in self.chars:
            if ord(self.minChar) > ord(c):
                self.minChar = c

        return self.minChar

chars = ['c', 'x', 'Q', 'A']
mi = MinAlgorithm(chars)
minChar = mi.getMinChar()
print(f'minChar : {minChar}')

9. 최빈값

빈도수가 가장 높은 데이터를 찾는 알고리즘

과정

1. 리스트의 가장 큰 값(최댓값)을 찾는다. (17)
2. 위에서 구한 최댓값(+1)만큼의 빈 배열 리스트를 만든다.
   (초기값: [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0] 인덱스 18개)
3. 기존 데이터의 값을 인덱스로 인식하여 빈 배열 리스트에 인덱스 값에 +1 씩 추가한다. (ex. nums에서 7은 인덱스7로 인식한 다음 indexes에서 인덱스7 자리에 빈도수만큼 추가함)
4. 리스트에서 1이 누적된 값중 가장 큰 값을 다시 최댓값 알고리즘을 이용하여 기존 리스트에서 최빈값을 구한다.

class MaxAlgorithm:

    def __init__(self,ns):
        self.nums = ns
        self.maxNum = 0
        self.maxNumIdx = 0

    def setMaxNumAndIdx(self):
        self.maxNum = self.nums[0]
        self.maxNumIdx = 0

        for i, n in enumerate(self.nums):
            if self.maxNum < n:
                self.maxNum = n
                self.maxNumIdx = i

    def getMaxNum(self):
        return self.maxNum
    def getMaxIdx(self):
        return self.maxNumIdx

nums = [1, 3, 7, 6, 7, 7, 7, 12, 12, 17]
maxAlo = MaxAlgorithm(nums)
maxAlo.setMaxNumAndIdx()
maxNum = maxAlo.getMaxNum()
print(f'maxNum:{maxNum}')

indexes = [0 for i in range(maxNum+1)]
print(indexes)

for n in nums:
    indexes[n] = indexes[n] + 1
print(indexes)

maxAlo = MaxAlgorithm(indexes)
maxAlo.setMaxNumAndIdx()
maxNum = maxAlo.getMaxNum()
maxNumIdx = maxAlo.getMaxIdx()
print(f'{maxNumIdx}의 숫자가 {maxNum}의 빈도수로 가장 높다')

#실행결과 
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 1, 0, 1, 0, 0, 1, 4, 0, 0, 0, 0, 2, 0, 0, 0, 0, 1]
7의 숫자가 4의 빈도수로 가장 높다

10. 근삿값

특정 값과 가장 가까운 값을 찾는 알고리즘

특정 값과 순서대로 값을 비교하면서 차이가 가장 적은 값을 찾아가는 과정이다.

import random

nums = random.sample(range(0,50),20)
print(f'nums:{nums}')

inputNum = int(input('숫자를 입력하세요:'))
nearNum = 0 #근삿값 변수 
maxNum = 50 #nums의 범위최댓값이 50이라는 변수 

for n in nums:
    absNum = abs(n - inputNum)
    if absNum < maxNum:
        maxNum = absNum
        nearNum = n
print(f'{inputNum}의 근삿값은 {nearNum}입니다')

#실행결과 
nums:[32, 1, 13, 17, 45, 46, 14, 0, 23, 28, 24, 26, 33, 29, 18, 15, 36, 47, 35, 43]
숫자를 입력하세요:44
44의 근삿값은 45입니다

11. 평균

평균을 구하는 알고리즘

• 1부터 100까지 50개의 난수를 뽑아 그중 50이상 100미만 숫자들의 평균을 구하는 코드

import random

nums = random.sample(range(1,100),50)

total = 0
targetNums = []

for n in nums:
    if n > 50 and n < 100:
        total += n
        targetNums.append(n)

average = total / len(targetNums)
print(f'targetNums:{targetNums}')
print(f'average: {round(average,2)}')

#실행결과 
targetNums:[81, 75, 71, 74, 79, 59, 86, 87, 94, 82, 89, 51, 80, 55, 78, 53, 52, 76, 64, 77, 88, 93, 67, 69]
average: 74.17

12. 재귀 알고리즘

자기 자신을 호출하는 알고리즘

• 반복문을 이용하지않고 재귀알고리즘을 이용하여 별찍기

def recusion(num):

    if num > 0:
        print('*'* num)
        return recusion(num-1)
    else:
        num = 1

recusion(10)

• 팩토리얼 구하기

def factorial(num):
    if num > 0:
        return num * factorial(num-1)
    else:
        return 1

print(f'factorial(10):{factorial(10)}')
#실행결과 
factorial(10):3628800

• 재귀함수를 이용하여 최대공약수 구하기

def gcd(n1,n2):

    if n1 % n2 == 0:
        return n2
    else:
        return gcd(n2, n1 % n2)

print(f'gcd(82,32):{gcd(82,32)}')

13. 재귀함수를 이용해 하노이의 탑 구현

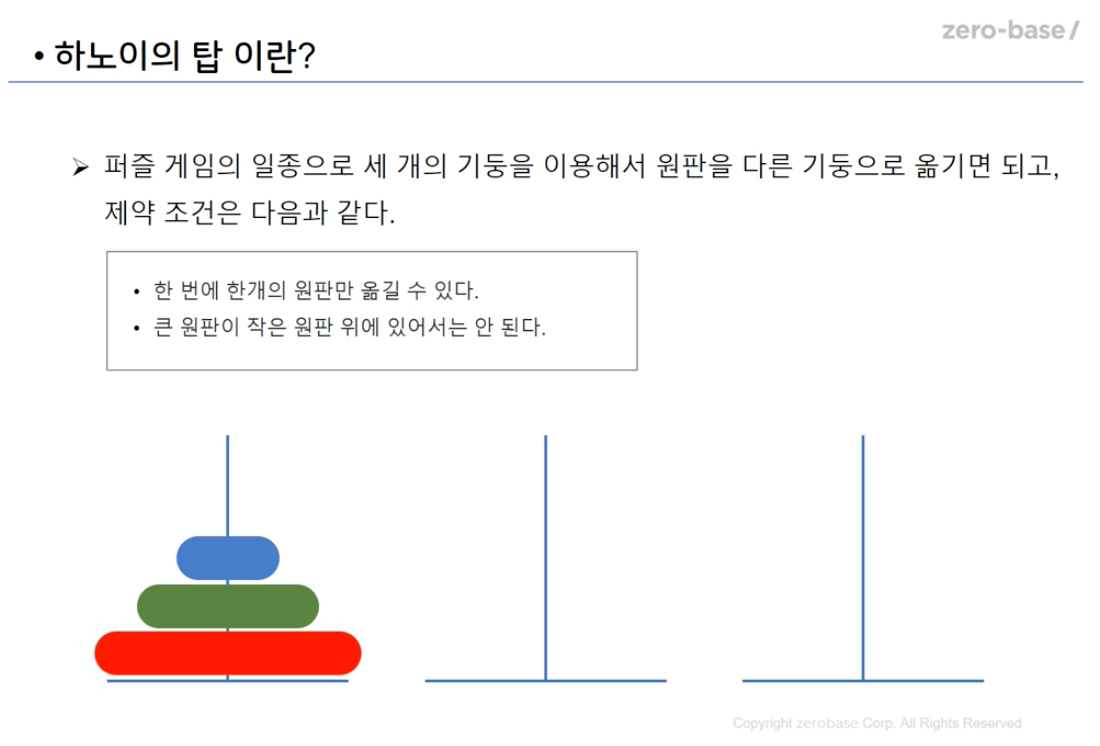
def moveDisc(discCnt, fromBar, toBar, viaBar):
    if discCnt == 1:
        print(f'{discCnt}disc를 {fromBar}에서 {toBar}으로 이동')

    else:
        #(discCnt-1)개들을 경유 기둥으로 이동 
        moveDisc(discCnt -1, fromBar, viaBar, toBar)
        
        #discCnt를 목적 기둥으로 이동
        print(f'{discCnt}disc를 {fromBar}에서 {toBar}으로 이동')
        
        #(discCnt-1)개들을 도착 기둥으로 이동 
        moveDisc(discCnt -1, viaBar, toBar, fromBar)

moveDisc(3,1,3,2)

14. 병합정렬

자료구조를 더이상 쪼갤 수 없을 때까지(즉 숫자의 갯수가 2보다 작을때까지) 분할한뒤, 다시 하나하나 크고 작음을 비교하여 병합하여 정렬하는 알고리즘

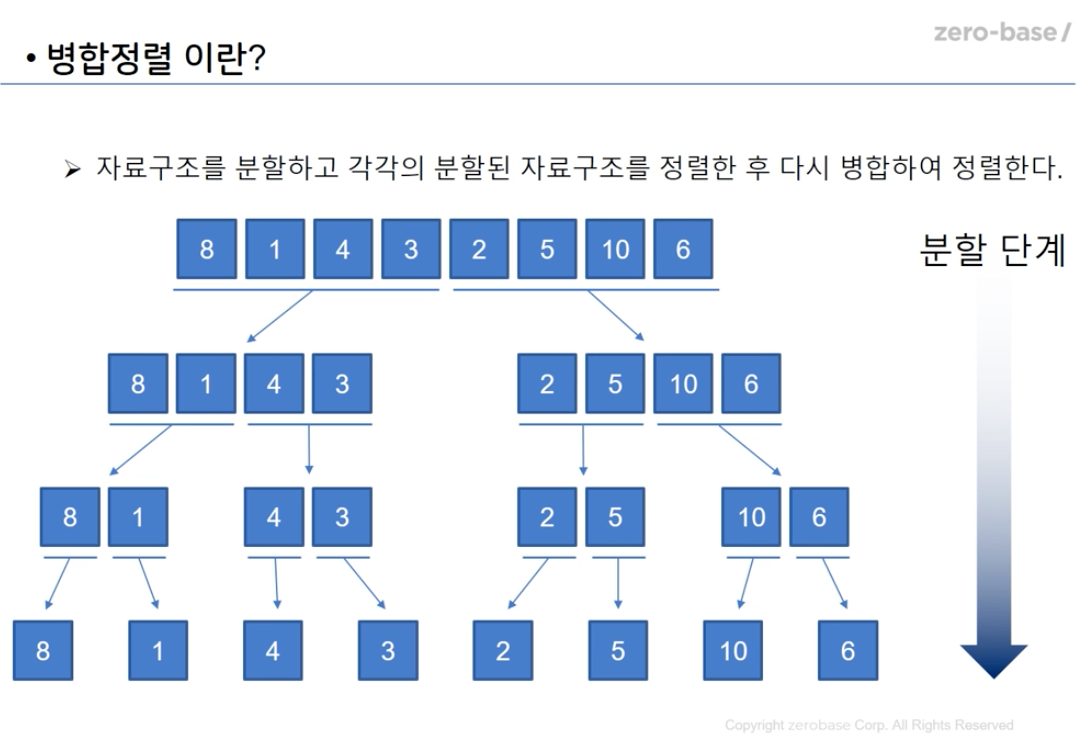
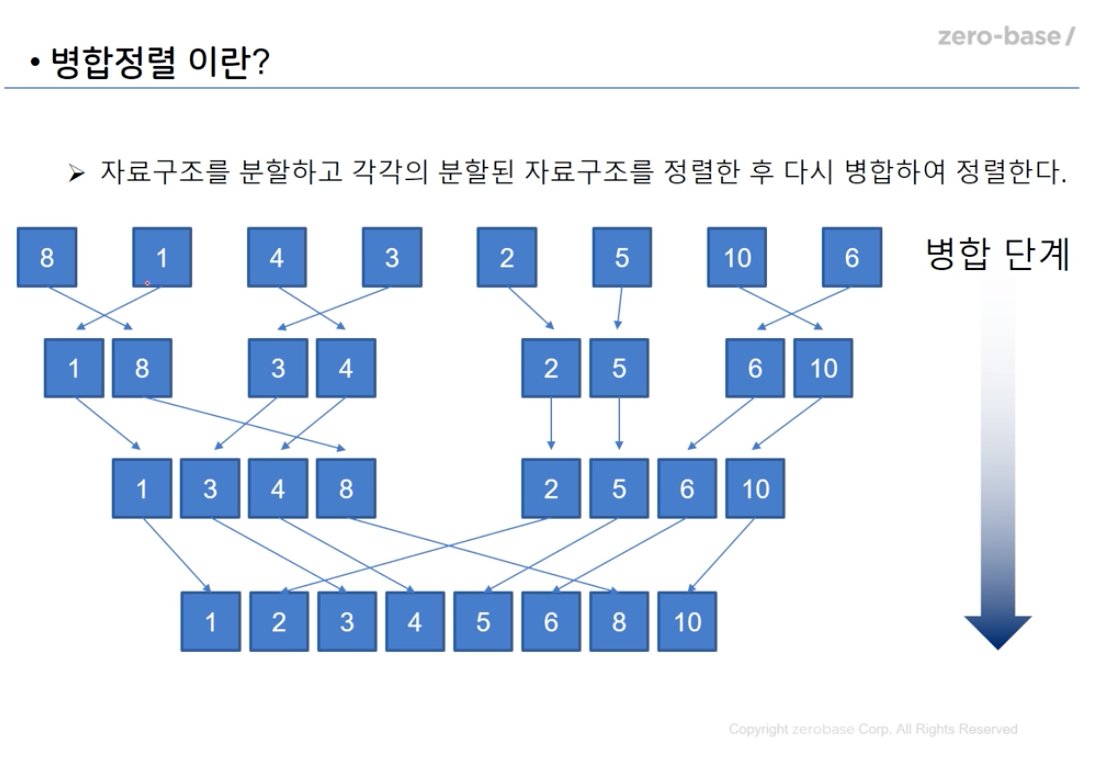
def mSort(ns):

    if len(ns) <2:
        return ns

    midIdx = len(ns) //2
    leftNums = mSort(ns[0:midIdx])
    rightNums = mSort(ns[midIdx : len(ns)])

    mergeNums = []
    leftIdx = 0; rightIdx = 0
    while leftIdx < len(leftNums) and rightIdx < len(rightNums):
        if leftNums[leftIdx] < rightNums[rightIdx]:
            mergeNums.append(leftNums[leftIdx])
            leftIdx +=1

        else:
            mergeNums.append(rightNums[rightIdx])
            rightIdx +=1

    mergeNums = mergeNums + leftNums[leftIdx:]
    mergeNums = mergeNums + rightNums[rightIdx:]

    return mergeNums

nums = [8, 1, 4, 3, 2, 5, 10, 6]
print(f'mSortNums : {mSort(nums)}')

15. 퀵정렬

기준키를 기준으로 작거나 같은 값을 지닌 데이터는 앞으로, 큰 값을 지닌 데이터는 뒤로 가도록 하여 작은 값을 갖는 데이터와 큰 값을 갖는 데이터로 분리해가며 정렬하는 방법

def quickSor

    midIdx = len(ns) // 2
    midVal = ns[midIdx]

    smallNums = []; sameNums = []; bigNums =[]

    for n in ns:t(ns):

    if len(ns) < 2:
        return ns
        if n < midVal:
            smallNums.append(n)

        elif n == midVal:
            sameNums.append(n)

        elif n > midVal:
            bigNums.append(n)

    return quickSort(smallNums)+sameNums+quickSort(bigNums)

nums = [ 1,2,4,8,5,8,9,10,3,7]
result = quickSort(nums)
print(result)