파이썬-기초 수학

1. 수열

규칙성을 가지고 나열되어 있는 수들.

2, 4, 6, 8, 10...

위에서 나열되 있는 수를 형식(일반항)으로 표현해보면 다음과 같다

a𝚗 = 2n
여기서 2n이 바로 일반항을 의미한다.

2. 등차수열

수열에서 중요한것은 바로 규칙성을 가지고 있다는 것이다. 등차수열은 연속된 두 항의 차이가 일정한 수열을 의미한다.

2, 4, 6, 8, 10...

위의 수열의 예문과 똑같은데 위가 바로 등차수열이다. 두 항의 차이가 2인 등차수열이라고 할 수 있다. 여기에서 두 항의 차이는 공차라고 부른다.
그렇다면 위 예문은 공차가 2인 등차수열이 되는 것 이다.

등차 수열의 일반항
an = a1 + (n-1) * d

3. 등차 중항

연속된 세 항에서 가운데 항

5, 9, 13, 17, 21, 25, 29, 33

위는 공차가 4인 등차수열이다. 등차 중항을 구하려면 구하려는 항의 양 옆의 항을 더한것의 1/2 값이 등차 중항이 된다.

예를 들어 위 수열에서 값 17은 양 옆의 수 13과 21을 더한 값인 34의 2/1값이 되는 것이다.

4. 등차수열의 합 구하기

등차수열의 규칙성을 이용하여 모든 항들의 총합을 구할 수 있다.

Sn = n(a1+an) / 2

등차수열의 합(Sn)은 첫째항(a1) 과 n번째항(an) 의 합을 n으로 곱한 값을 2로 나눈 값이다.

5. 등차수열 with Python

이제 수열과 등차수열, 등차수열의 일반항, 등차수열의 합을 알아보았으니 파이썬을 통해서 어떻게 등차수열을 출력할 수 있는지 알아보겠다.

inputN1 = int(input('a1 입력:'))
inputD = int(input('공차 입력:'))
inputN = int(input('n 입력:'))
valueN = 0 #N번째 항
n = 1
while n <= inputN:
    if n == 1:
        valueN = inputN1
        print('{}번째 항의 값: {}'.format(n,valueN))
        n+=1
        continue
    valueN += inputD
    print('{}번째 항의 값: {}'.format(n,valueN))
    n+=1
print('{}번째 항의 값: {}'.format(inputN, valueN))
#실행결과 
a1 입력:2
공차 입력:3
n 입력:7
1번째 항의 값: 2
2번째 항의 값: 5
3번째 항의 값: 8
4번째 항의 값: 11
5번째 항의 값: 14
6번째 항의 값: 17
7번째 항의 값: 20
7번째 항의 값: 20

등차수열을 파이썬으로 출력할때는 while 문을 이용하여 구한다.

6. 등차수열 with Python

inputN1 = int(input('a1 입력:'))
inputD = int(input('공차 입력:'))
inputN = int(input('n 입력:'))
valueN = inputN1 + (inputN - 1) * inputD
print('{}번째 항의 값: {}'.format(inputN, valueN))
#실행결과 
a1 입력:2
공차 입력:3
n 입력:7
7번째 항의 값: 20

7. 등차수열의 합 구하기 with Python

• 다음 수열의 n번째 항까지의 합을 출력하는 프로그램을 만들어보자

inputN1 = int(input('a1 입력:'))
inputD = int(input('공차 입력:'))
inputN = int(input('n 입력:'))
valueN= 0
sumN= 0
n=1
while n <= inputN:
    if n == 1:
        valueN = inputN1 
        sumN += valueN 
        print('{}번째 항까지의 합: {}'.format(n,sumN))
        n += 1
        continue
    valueN += inputD
    sumN += valueN
    print('{}번째 항까지의 합: {}'.format(n, sumN))
    n += 1
print('{}번째 항까지의 합: {}'.format(inputN,sumN))

위에서 등차수열의 값 while문을 통해 구하는 코드에서 sumN (N번째 항까지의 합)이 추가된 것을 알 수 있다.

8. 등차수열의 합 구하기 with Python(공식 이용)

• 다음 수열의 n번째 항까지의 합을 구하는 공식을 이용하여 등차수열의 합을 출력하는 프로그램을 만들어보자

inputN1 = int(input('a1 입력:'))
inputD = int(input('공차 입력:'))
inputN = int(input('n 입력:'))
valueN = inputN1 + (inputN-1) * inputD
sumN = inputN*(inputN1+valueN) / 2
print('{}번째 항까지의 합: {}'.format(inputN,int(sumN)))

이것 또한 위에서 등차수열의 합을 구하는 공식을 대입하여 풀면 훨씬 간결하게 코드를 출력할 수 있다.

9. 등비수열

연속된 두항의 비가 일정한 수열

2, 6, 18, 54, 162, 486, 1458...

위 수열에서 두항의 비가 3임을 알수 있다. 여기서의 두항의 비는 공비(r)로 표현할 수 있고 이 수열은 두항의 비가 3인 등비수열이라고 부를 수 있다.

등비수열 일반항 공식
an = a1 * r^(n-1)

10. 등비 중항

위에서 등차중항의 값을 배운 것처럼 등비수열에서의 등비중항을 구하는 방법은 구하려는 항 양 옆의 수를 곱하여 나온값이 구하려는 값의 제곱이 된다.

2, 6, 18, 54, 162, 486, 1458...

즉, 위의 등비수열을 다시 보면 '54'는 양옆 18과 162를 곱한 값이 54의 제곱이 되는 값과 동일하다.
18 x 162 = 1,916
54 x 54 = 1,916
등차중항은 양 옆의 값을 더했는데 등비중항은 곱한다고 생각하면 되겠다.

11. 등비수열의 합 공식

등비수열의 합도 마찬가지로 규칙성을 이용해서 모든 항들의 총합을 구할 수 있다.

Sn = a1 * (1-(r^n)) / (1-r)

12. 등비수열 구하기 with Python

• 다음 수열의 n번째 항의 값을 출력하는 프로그램을 만들어보자
  an = {2, 4, 8, 16, 32, 64, 128....}

inputN1 = int(input('a1 입력:'))
inputR = int(input('공비 입력:'))
inputN = int(input('n 입력:'))
valueN = 0
n = 1
while n <= inputN:
    if n == 1:
        valueN = inputN1
        print('{}번째 항의 값:{}'.format(n,valueN))
        n+=1
        continue
    valueN *= inputR
    print('{}번째 항의 값: {}'.format(n,valueN))
    n+=1
print('{}번째 항의 값: {}'.format(inputN,valueN))
#실행결과 
a1 입력:2
공비 입력:2
n 입력:7
1번째 항의 값:2
2번째 항의 값: 4
3번째 항의 값: 8
4번째 항의 값: 16
5번째 항의 값: 32
6번째 항의 값: 64
7번째 항의 값: 128
7번째 항의 값: 128

while문을 이용하면 등차수열의 값을 구하는 것과 동일하게 while문을 이용하여 구할 수 있고 코드또한 유사하게 작성하면 된다. 등비는 곱해야하므로 n번째 항의 값에 n번째까지 공비(R)값을 곱하여 대입시키면 되겠다.

13. 등비수열 구하기 with Python(공식 이용)

inputN1 = int(input('a1 입력:'))
inputR = int(input('공비 입력:'))
inputN = int(input('n 입력:'))
valueN = inputN1 * inputR ** (inputN - 1)
print('{}번째 항의 값: {}'.format(inputN,valueN))
#실행결과 
a1 입력:2
공비 입력:2
n 입력:7
7번째 항의 값: 128

등비수열의 값을 구하는 공식(an = a1 * r^(n-1))을 대입시키면 좀더 간결하게 코드를 구현할 수 있다.

14. 등비수열의 합 구하기 with Python

• 다음 수열의 n번째 항까지의 합을 출력하는 프로그램을 만들어보자
  an = {5, 15, 45, 135, 405, 1215, 3645...}

inputN1 = int(input('a1 입력:'))
inputR = int(input('공비 입력:'))
inputN = int(input('n 입력:'))
valueN = 0
sumN = 0
n = 1
while n <= inputN:
    if n == 1:
        valueN = inputN1
        sumN += valueN
        print('{}번째 항까지의 합: {}'.format(n,sumN))
        n+=1
        continue
    valueN *= inputR
    sumN += valueN
    print('{}번째 항까지의 합: {}'.format(n, sumN))
    n += 1
print('{}번째 항까지의 합 {}'.format(inputN,sumN))
#실행결과 
a1 입력:5
공비 입력:3
n 입력:7
1번째 항까지의 합: 5
2번째 항까지의 합: 20
3번째 항까지의 합: 65
4번째 항까지의 합: 200
5번째 항까지의 합: 605
6번째 항까지의 합: 1820
7번째 항까지의 합: 5465
7번째 항까지의 합 5465

15. 등비수열의 합 구하기 with Python(공식 이용)

• 다음 수열의 n번째 항까지의 합을 출력하는 프로그램을 만들어보자

inputN1 = int(input('a1 입력:'))
inputR = int(input('공비 입력:'))
inputN = int(input('n 입력:'))
sumN = inputN1 * (1-(inputR ** inputN)) / (1-inputR)
print('{}번째 항 까지의 합 {}'.format(inputN,int(sumN)))
#실행결과 
a1 입력:5
공비 입력:3
n 입력:7
7번째 항 까지의 합 5465

등비수열의 합을 구하는 공식(Sn = a1 * (1-(r^n)) / (1-r)) 을 이용하여 등비수열의 합을 구하였다.

16. 시그마

∑란, 수열의 합을 나타낸 기호

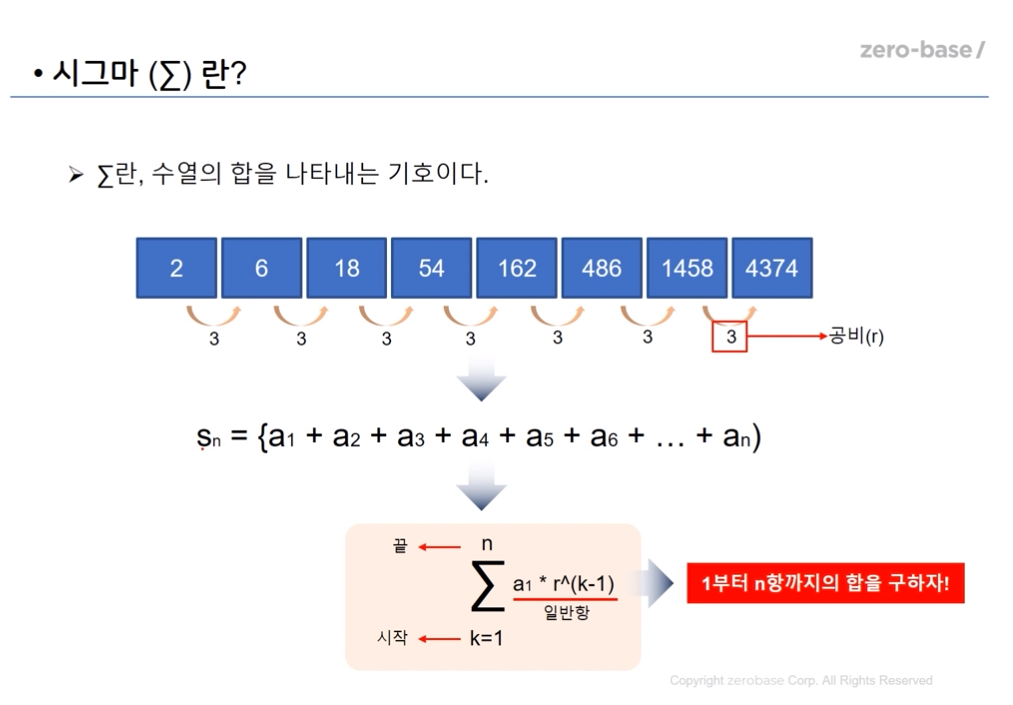
시그마라는 기호를 읽는 법은, 시작점인 k=1 즉 1항부터 끝항인 n번째 항까지의 합을 구한다라고 이해하면 된다. 그 다음 이 수열이 어떤 수열인지 확인을 하려면 일반항 부문을 보면 되고 등비수열인지 등차수열인지를 확인 한 후 위에서 배운 공식을 대입하여 구하면 되겠다.

17. 계차 수열

어떤 수열의 인접하는 두항의 차로 이루어진 또 다른 수열

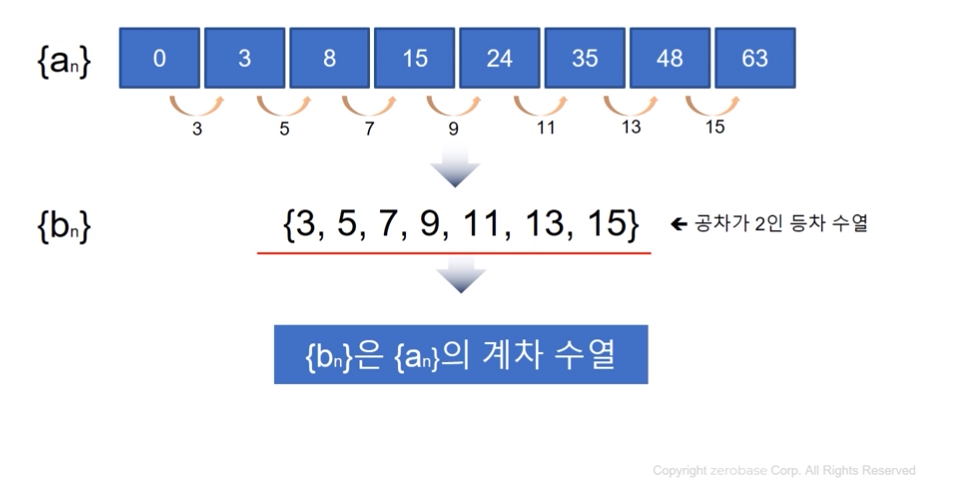
bn은 an의 계차 수열이라고 말할 수 있다. 이때 위의 예제 수열을 보면 bn은 일정한 공차를 갖고있는 등차 수열을 나타내고 있다.

18. 계차 수열의 일반항 구하기

계차 수열을 이용해서 수열 an의 일반항을 구할 수 있고 그 공식은 다음과 같다.

an = n^2 + n + 1

19. 계차 수열의 값 구하기 with Python

• 다음 수열을 보고 n번째 항의 값을 출력하는 프로그램을 만들어보자
  an = {3, 7, 13, 21, 31, 43, 57...}

inputAN1 = int(input('a1 입력:'))
inputAN = int(input('an 입력:'))
inputBN1 = int(input('b1 입력:'))
inputBD = int(input('bn 공차 입력:'))
valueAN = 0
valueBN = 0
n = 1
while n <= inputAN:
    if n == 1:
        valueAN = inputAN1
        valueBN = inputBN1
        print('an의 {}번째 항의 값:{}'.format(n,valueAN))
        print('bn의 {}번째 항의 값:{}'.format(n, valueBN))
        n+=1
        continue
    valueAN += valueBN
    valueBN += inputBD
    print('an의 {}번째 항의 값:{}'.format(n, valueAN))
    print('bn의 {}번째 항의 값:{}'.format(n, valueBN))
    n+=1
print('an의 {}번째 항의 값 {}'.format(inputAN,valueAN) )
print('bn의 {}번째 항의 값 {}'.format(inputAN,valueBN))
#실행결과 
a1 입력:3
an 입력:14
b1 입력:4
bn 공차 입력:2
an의 1번째 항의 값:3
bn의 1번째 항의 값:4
an의 2번째 항의 값:7
bn의 2번째 항의 값:6
an의 3번째 항의 값:13
bn의 3번째 항의 값:8
an의 4번째 항의 값:21
bn의 4번째 항의 값:10
an의 5번째 항의 값:31
bn의 5번째 항의 값:12
an의 6번째 항의 값:43
bn의 6번째 항의 값:14
an의 7번째 항의 값:57
bn의 7번째 항의 값:16
an의 8번째 항의 값:73
bn의 8번째 항의 값:18
an의 9번째 항의 값:91
bn의 9번째 항의 값:20
an의 10번째 항의 값:111
bn의 10번째 항의 값:22
an의 11번째 항의 값:133
bn의 11번째 항의 값:24
an의 12번째 항의 값:157
bn의 12번째 항의 값:26
an의 13번째 항의 값:183
bn의 13번째 항의 값:28
an의 14번째 항의 값:211
bn의 14번째 항의 값:30
an의 14번째 항의 값 211
bn의 14번째 항의 값 30

an의 14번째 항의 값은 211이라는 값을 알 수 있다.

20. 계차 수열의 값 구하기 with Python (공식 이용)

• 다음 수열을 보고 n번째 항의 값을 출력하는 프로그램을 만들어보자
  an = {3, 7, 13, 21, 31, 43, 57...}

inputAN1 = int(input('a1 입력:'))
inputAN = int(input('an 입력:'))
valueAN = inputAN ** 2 + inputAN + 1
print('an의 {}번째 항의 값: {}'.format(inputAN,valueAN))
#실행결과 
a1 입력:3
an 입력:14
an의 14번째 항의 값: 211

계차수열의 일반항 구하는 공식(an = n^2 + n + 1)을 대입하여 파이썬 코드를 작성하면 위와 같이 쉽게 an의 값을 구할 수 있다.

21. 피보나치 수열

세번째 항은 두번째 항과 첫 번째 항을 더한 합이다.

1, 1, 2, 3, 5, 8, 13, 21

위 수열을 보면 세번째항은 첫번째항 1과 두번째항 1을 합친 값과 같고 4번째항인 3은 두번째 항 1과 세번째항 2를 합친것과 같다.
즉, an = (an-2) + (an-1) 이 되는것이다. 해석하면 피보나치의 수는 구하려는 피보나치의 수의 그 전항과 전전항을 더한 것과 같다고 할 수 있다.

22. 피보나치의 수 구하기 with Python

inputN = int(input('n 입력:'))
valueN = 0 # N번째 항의 값
sumN = 0
valuePreN2 = 0 # N번째 항의 이전값
valuePreN1 = 0
n = 1
while n <= inputN:
    if n == 1 or n == 2:
        valueN = 1
        valuePreN2 = valueN
        valuePreN1 = valueN
        sumN += valueN
        n+=1
    else:
        valueN = valuePreN2 + valuePreN1
        valuePreN2 = valuePreN1
        valuePreN1 = valueN
        sumN += valueN
        n+=1
print('{}번째 항의 값: {}'.format(inputN,valueN))
print('{}번째 항까지의 값: {}'.format(inputN,sumN))
#실행결과 
n 입력:9
9번째 항의 값: 34
9번째 항까지의 값: 88

23. 팩토리얼

1부터 양의 정수 n까지의 정수를 모두 곱한것

3! → 1 x 2 x 3 = 6
4! → 1 x 2 x 3 x 4 = 24
(이때 0!은 1로 약속한다.)

팩토리얼을 구하는 가장 기본적인 방법은 for문을 이용하는 것이고 두번째로는 math 함수인 내장함수를 이용하는 방법이다.

• for 문을 이용하여 팩토리얼을 구하는 방법

inputN = int(input('n 입력:'))
result = 1
for n in range(1, (inputN+1)):
    result *= n
print('{}의 팩토리얼: {}'.format(inputN, result))
#실행결과 
n 입력:4
4의 팩토리얼: 24

• factorial math 함수를 이용하여 팩토리얼을 구하는 방법

inputN = int(input('n 입력:'))
import math
print('{}의 팩토리얼: {}'.format(inputN, math.factorial(inputN)))
#실행결과 
n 입력:4
4의 팩토리얼: 24

24. 군수열

여러 개의 항을 묶었을 때 규칙성을 가지는 수열

• 50번째 항의 값을 구해보자
  예제를 보면 항을 묶었을 때의 규칙성은 공차가 1인 등차수열임을 알 수 있다.
  이것을 공식에 대입해보면 an 은 n 이며 n번째 항까지의 합(Sn)은 n(a1 + an) / 2 에 n을 대입했을때 n^2 + n / 2 라는 것을 알 수 있다. 그렇다면 9항을 n 값에 한번 대입해보면

(9 x 9 + 9) / 2 = 45 라는 값이 나오는 것을 알 수 있는데 이 45가 9군의 45번째 항이라는 의미이다. 그럼 우리가 구하고자하는 값은 50번째 항이므로 10군의 5항을 찾으면 50번째가 된다. 즉 50번째 항은 5라는 것을 알 수 있다.

25. 군수열 with Python

• 다음 수열을 보고 n번째 항의 값을 출력하는 프로그램을 만들어보자.
  1, 1, 2, 1, 2, 3, 1, 2, 3, 4, 1, 2, 3, 4, 5,...

inputN = int(input('n항 입력:'))
flag = True
n = 1
nCnt = 1
searchN = 0
while flag:
    for i in range(1,(n+1)):
        if i == n:
            print('{}'.format(i), end='')
        else:
            print('{}'.format(i), end='')
        nCnt += 1
        if (nCnt > inputN):
            searchN = i
            flag = False
            break
    print()
    n += 1
print('{}항: {}'.format(inputN, searchN))