1. 로지스틱 회귀분석(Logistic Function)
- 입력 변수가 여러 종류일 때: 다중 로지스틱 회귀
2. 회귀계수 축소법
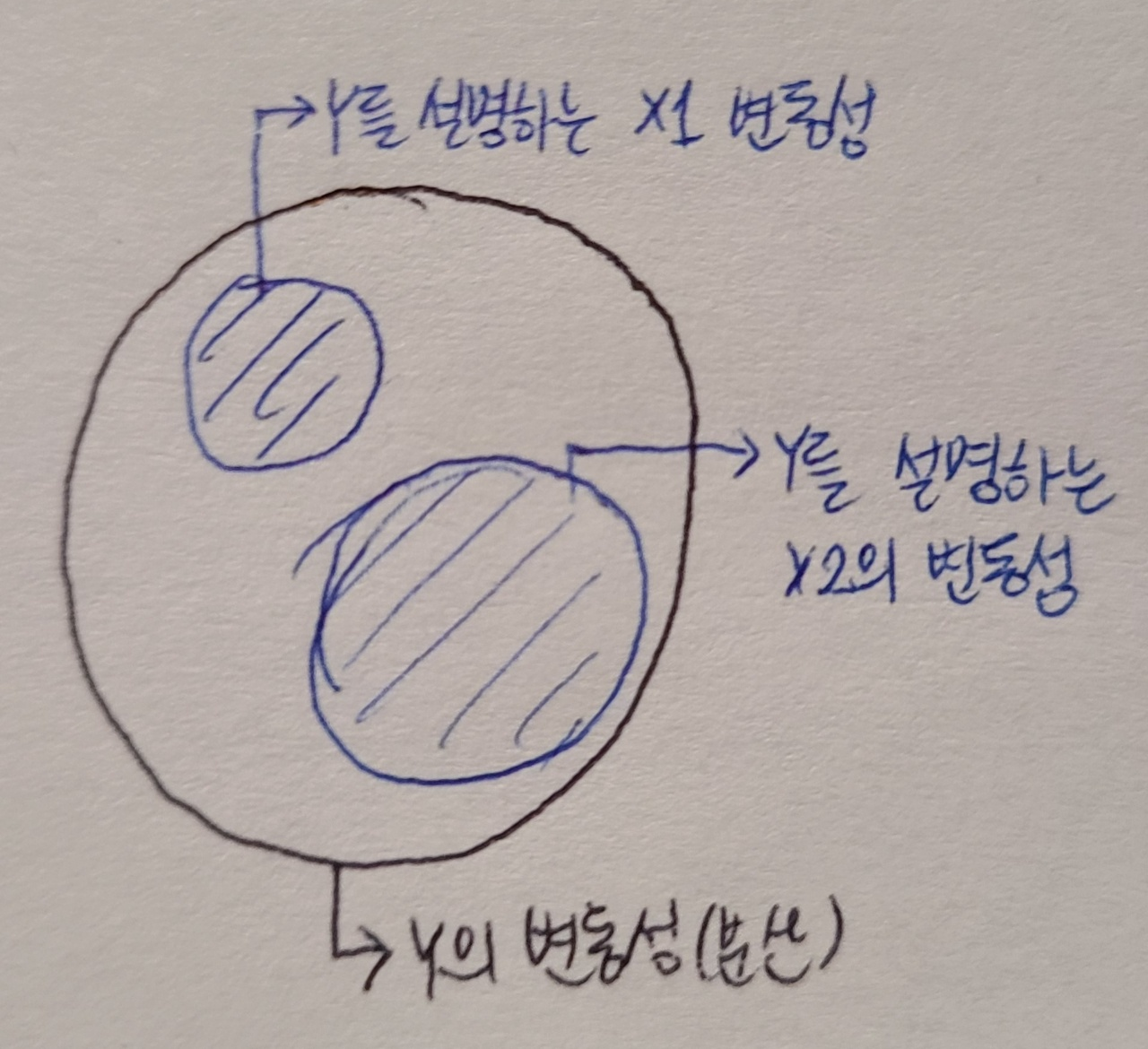
[1] 좋은 변수는?
- Y의 변동성을 잘 설명하면서 + 상관관계가 없는 변수들
[2] 회귀계수를 축소하는 이유
: 영향력이 없는 입력 변수의 계수를 0에 가깝게 가져간다면, 모형에 포함되는 입력 변수의 수를 줄일 수 있음
> 입력 변수 수를 줄였을 때 장점
- noise 제거 -> 모형 정확도 개선
- 모형 연산 속도 증가
- 다중공선성의 문제 완화 -> 모형의 해석 능력 향상
[3] 계수축소법 종류
다중 선형 회귀 vs 로지스틱 회귀
- 다중 선형 회귀: 잔차 최소화
minimize SSE- 로지스틱 회귀: 잔차 + 회귀계수 최소화
minimize SSE + f(b)
종류 3가지
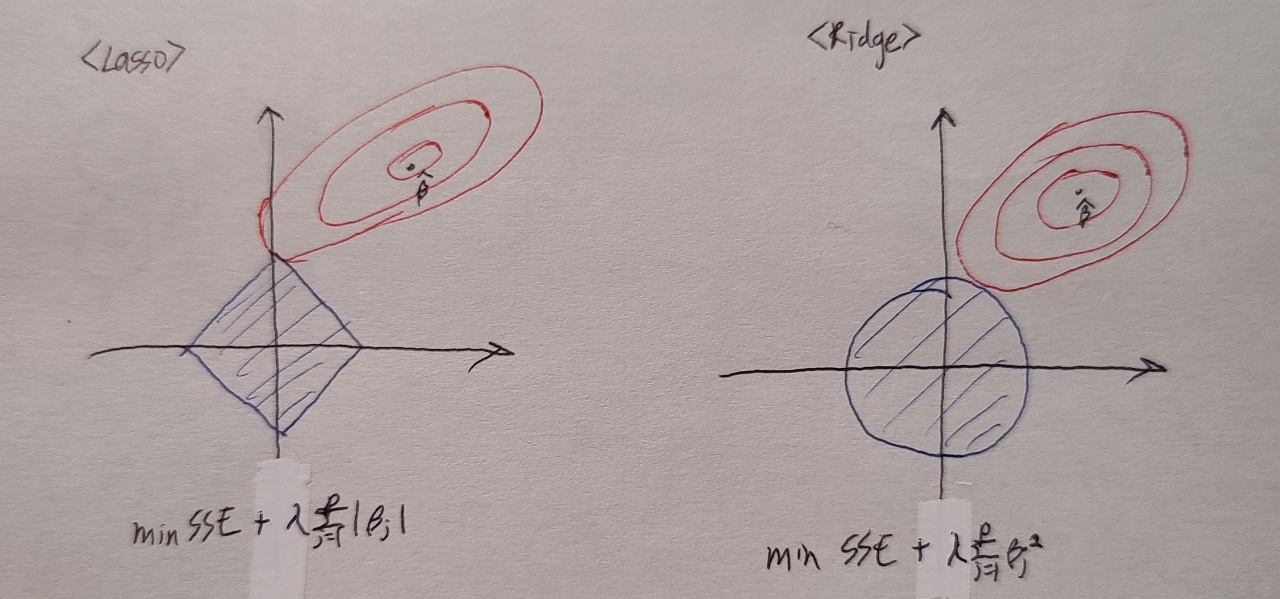
1) Ridge 회귀
- f(b): 회귀계수의 제곱의 합
- 람다(tuning parameter)가 클수록 보다 많은 회귀계수를 0으로 수렴(완전히 0이 되지는 않음)
2) Lasso 회귀
- f(b): 회귀계수의 절대값의 합
- 람다(tuning parameter)가 클수록 보다 많은 회귀계수를 0으로 수렴(완전히 0이 됨)
람다(lambda)값 설정
람다 값을 변화시켜가며 MSE가 최소일 때 람다를 탐색
Ridge vs Lasso
3) Elastic-Net 회귀
- Ridge와 Lasso회귀의 하이브리드(정규화) 회귀 모델