1. Naive byes Classifier
종류
- 설명변수가 연속형: 가우시안 나이브 베이지안
- 설명변수가 범주형: Multinomial 나이브 베이지안
- 설명변수가 이분형: Bernoulli 나이브 베이지안
2. KNN
1) Distance d(a,b) 선택
- 범주형 변수: Hamming distance
- 연속형 변수: Euclidian distance, Manhattan distance
2) Cross-Validation
- error를 과소추정하지 않으면서, 데이터 소실을 최소화하는 것. 데이터를 나누어 번갈아 가며 Training과 Test Set 역할을 함
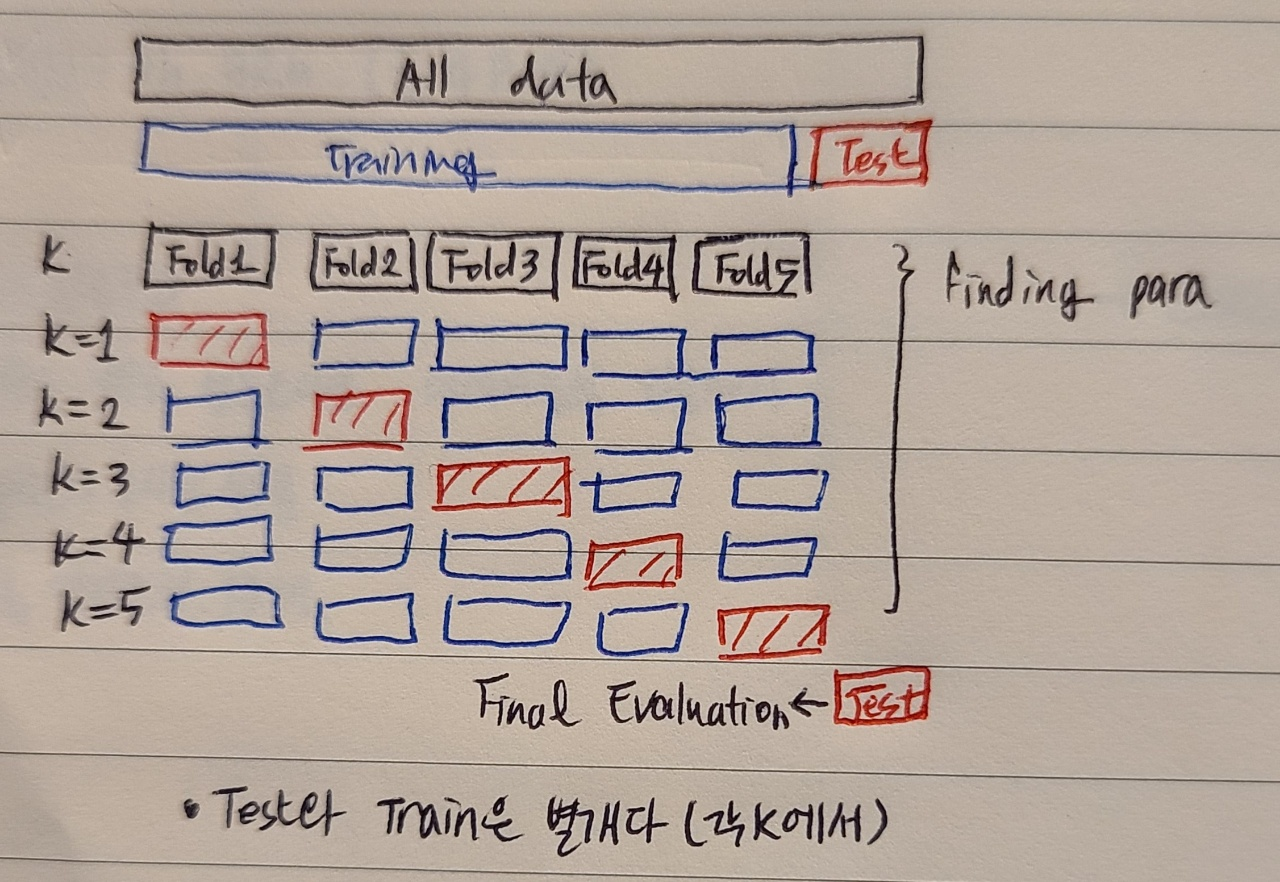
해결하고자 하는 문제 2가지
1. 과접합 문제
2. Smaple Loss
- Training set을 가장 잘 맞히는 머신은 Test set에서는 잘 작동하지 않을 수 있음
- Training error는 error를 과소추정하는 성향이 있음(training error로 판단하면 너무 복잡한 모델을 고르게 됨->Test error가 높아짐->좋은 모델이 아님)
(K가 크다= 모델이 덜 복잡하다)- test error로 판단하려면: 데이터를 나눠야 하므로 데이터 소실이 발생 -> 데이터 소실 완화하는 방법이 바로 cross-validation
3) K의 결정
- 너무 큰 k
- 미세한 경계부분 분류가 아쉬울 것
- 너무 작은 k
- 과적합 우려
- 이상치의 영향을 크게 받을 것
- 패턴이 직관적이지 않을 것
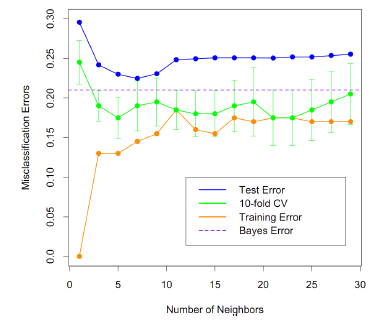
*그림출처: 패스트캠퍼스 Chapter08.KNN 교안
a) K=1: 과적합(Training error=0, Test Error는 가장 큼= 새로운 데이터(Test data)를 거의 예측하지 못함)
b) Training Error: K 증가함에 따라 증가(모델이 점점 덜 복잡해짐)
c) Test Error: 감소하다가 증가함! 가장 error가 작은 지점을 k로 결정
4) 차원의 저주
- 차원이 증가함에 따라 설명할 수 있는 부분이 적어짐
<예시>
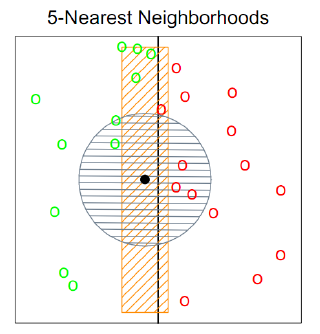
- x축에 정사영하면, 까만 점 주변에 녹색4개, 빨간색1개 -> 녹색으로 처리
- (차원추가)y축 기준으로, 까만 점 주변에 거리계산(원주)하면 녹색 2개, 빨간색 3개 -> 빨간색 처리
- 발생 원인: 쓸데 없는 변수가 추가되서
3. SVM
1) 종류
- 종속변수 데이터 형태에 따라 나뉨
a) 범주형 변수: SV Classifier
b) 연속형 변수: SV Regressiong(SVR)
2) SVM, SVR 핵심
- model cost에 영향을 끼칠 점과 끼치지 않을 점을 margin을 통해 구분
3) Largrange multiplier
- 라그랑주 승수의 기본 아이디어
: 최적화 문제를 풀때, f(x,y)를 최대화 하는 동시에 g(x,y)=c로 한정하고 싶은 경우
4. DT
- 변수들로 기준을 만들고 이것을 통하여 샘플을 분류하고 분류된 집단의 성질을 통하여 추정하는 모형
- 장점: 해석력 높음/직관적/범용성
- 단점: 변동성 높음/샘플에 민감할 수 있음
1) 종류
- 반응변수에 따라
a) 범주형 변수: 분류 트리(Classification Tree)
b) 연속형 변수: 회귀 트리(Regression Tree)
2) 분류 트리(Classification Tree)
- 정의: Tree조건에 따라, x가 가질 수 있는 영역을 block으로 나누는 개념.
- 나누어진 영역안에 속하는 샘플의 특성을 통하여 Y를 추정
- 나누어둔 영역들에 대해 measure(엔트로피, 오분류율, 지니계수)를 가장 좋은 값으로 만드는 변수와 기준 선택
3) 회귀 트리(Regression Tree)
- 정의: Tree조건에 따라, x가 가질 수 있는 영역을 block으로 나누는 개념.
- 나누어진 영역안에 속하는 샘플의 특성을 통하여 Y를 추정
