1. 단순 회귀 분석
단순 선형 회귀 모델 검정
- 귀무 가설: b1 = 0(회귀계수는 0 = 변수의 설명력이 존재하지 않음)
- 대립가설: b1 =! 0 (설명력 있는 변수 존재함)
1) 회귀 분석은 Y의 변동성을 '독립변수'가 얼마나 잘 설명하느냐가 중요
2) 변수가 여러개 일때 각각 Y를 설명하는 변동성이 크면 좋은 변수 = p-value가 자연스레 낮아짐
2. 다중 선형 회귀 분석
다중선형 회귀 모델 검정
- 귀무 가설: b1 = b2= ... = bp = 0(모든 회귀계수는 0 = 변수의 설명력이 하나도 존재하지 않음)
- 대립가설: 하나의 회귀계수라도 0이 아님(설명력 있는 변수 존재함)
--> 기각 하기 너무 쉬운 가설
--> (b/c) 변수가 추가되면 추가 될수록 기각하기 쉬워짐

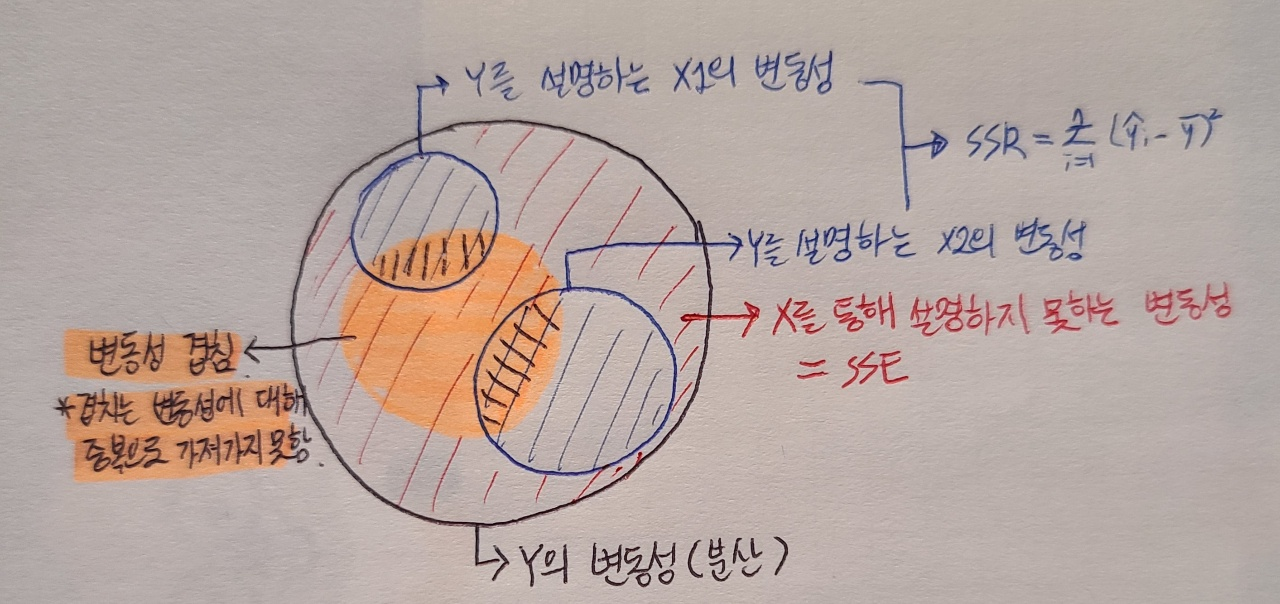
1) Y의 변동성: 총 변동은 정해져 있음(바뀌지 않음)
2) SSR
- 제곱합의 형태기 떄문에 변수가 추가되면 추가될수록 자연스럽게 증가함
- 제곱합의 형태로 검정을 하는 F검정의 특성상 변수가 추가되면 자연스럽게 기각하기 쉬워짐(R^2 증가)
다중 공선성(Multi-collinearity)
변수들간의 다중공선성이 있다
<문제점>
- 잘못된 변수 해석
- 예측 정화도 하락 등
<진단 방법>
- VIF, 변수간 Corr등으로 진단
<해결 방법>
: 중요한 변수 추출 방법은 데이터사이언스 분야에서 큰 이슈 중에 하나이다
- Feature Selection: 중요 변수만 선택
- 단순 변수 제거(corr 등 지표 활용)
- Lasso
- Stepwise
- 기타 변수 선택 알고리즘(유전 알고리즘 등)
- 변수 줄이지 않고 활용하는 방법
- AutoEncoder등의 Feature Extraction 기법(딥러닝 기법)
- PCA
- Ridge
3. 회귀분석 진단
- 회귀분석에는 잔차에 대한 3가지 가정 존재: 정규성, 독립성, 등분산성
- 3가지 가정을 만족할 경우 잘 만들어진 회귀모델이라 판단
- 잔차: 정규분포를 따름
- 일반적인 진단 방법
- Residuals 산점도
- Normal Q-Q plot
- Residuals vs fitted plot
잔차가 가정에 위배되는 경우
1) Y에 대하여 log 또는 루트 적용
2) 이상치 제거
3) 다항회귀분석: 항이 추가 될수록 overfitting 가능성 크므로, 고차항 추가시 신중해야 함