빅오, 자료형
컴퓨터과학에서 빅오(O)는 입력값이 커질 때 알고리즘의 실행 시간(시간 복잡도) 과 함께 공간 복잡도가 어떻게 증가하는지를 분류하는 데 사용되며, 알고리즘의 효율성을 분석하는 데에도 유용하게 활용됩니다.
빅오(O, big-O)는 "점근적 실행 시간(Asymptotic Running Time)"을 표기할 때 가장 널리 쓰이는 수학적 표기법 중 하나입니다.
점근적 실행 시간은 입력값 n이 무한대를 향할 때 함수의 실행 시간의 추이를 의미하고, 달리 말하면 "시간 복잡도(Time Complexity)"의 사전적 정의는 어떤 알고리즘을 수행하는 데 걸리는 시간을 설명하는 "계산 복잡도(Computational Complexity)"를 의미하며, 대표적인 표기 방법이 바로 빅오(O) 입니다.
시간 복잡도를 표현할 때는 최고차항만을 표기하며, 계수는 무시합니다.
예를 들어 4n^2 + 3n + 4일 경우, n^2가 됩니다. 따라서 점근적 표기법으로는 O(n^2)가 됩니다.
시간 복잡도를 표기할 때는 입력값에 따른 알고리즘의 실행 시간의 추이만 살피게 되고 종류는 크게 다음과 같습니다.
- O(1) : 입력값이 아무리 커도 실행 시간은 일정하며, 최고의 알고리즘이라 할 수 있습니다.
O(1)에 해당되는 알고리즘은 해시 테이블의 조회 및 삽입이 있습니다.
def is_sum(a: int) -> int:
return a + 23 # 파라미터가 아무리 커도 1번의 계산만 진행된다.- O(log n) : 여기서부터는 실행 시간은 입력값에 영향을 받습니다. 하지만 로그는 매우 큰 입력값에도 영향을 크게 받지 않는 편이며, 웬만한 n의 크기에 대해서도 매우 견고합니다.
대표적으로 "이진 검색(binary search)"가 이에 해당됩니다.
def B_search(arr: List[int],target: target):
low = 0
high = len(arr) - 1;
while(low <= high):
mid = (low + high) / 2;
if arr[mid] == target:
return mid
elif arr[mid] > target:
high = mid - 1
else
low = mid + 1
return -1
# 코드가 이해되지 않는다면 쉽게 up&down 게임으로 생각하면 이해하기 쉽다.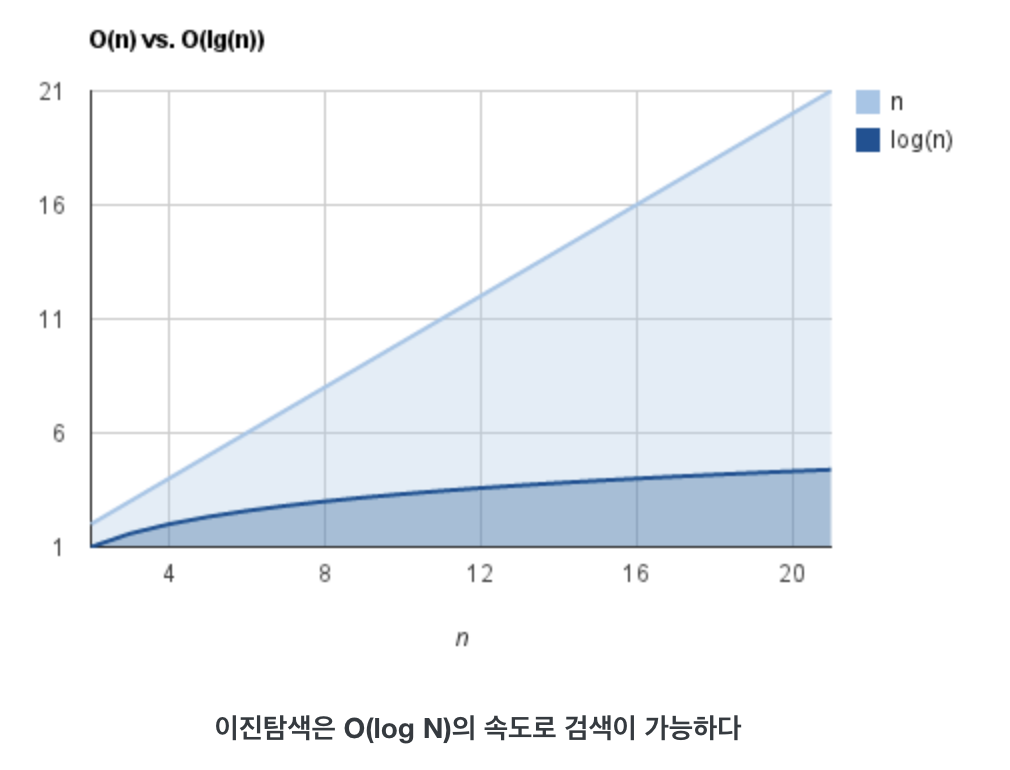
- O(n) : 입력값 n만큼 실핼 시간에 영향을 받으며, 이러한 알고리즘을 "선형 시간(Linear-Time)" 알고리즘이라고 합니다.
정렬되지 않은 리스트에 최대값 혹은 최소값을 찾는 경우가 해당됩니다.
def is_iterator_sum(n: int) -> int:
answer = 0
for num in range(a):
answer += num # n값 만큼 반복 계산
return answer- O(n log n) : 적어도 모든 수에 대해 한 번 이상은 비교해야 하는 비교 기반 정렬 알고리즘인 병합 정렬이 이에 해당하고, 비교를 건너뛰는 팀소트 알고리즘(Timsort-Algorithm)이 O(n)이 될 수 있습니다.
[팀소트 알고리즘이란? - 2002년 소프트웨어 엔지니어 Tim Peters에 의하여 Tim sort가 등장했다. 이 정렬 알고리즘은 Insertion sort와 Merge sort를 결합하여 정렬 알고리즘의 단점을 최대한 극복한, 많은 프로그래밍 언어에서 표준 정렬 알고리즘으로 채택되어 사용되고 있는 정렬이다. // 출처 - https://d2.naver.com/helloworld/0315536]
def insertion_sort(array, left=0, right=None):
if right is None:
right = len(array) - 1
# Loop from the element indicated by
# `left` until the element indicated by `right`
for i in range(left + 1, right + 1):
# This is the element we want to position in its
# correct place
key_item = array[i]
# Initialize the variable that will be used to
# find the correct position of the element referenced
# by `key_item`
j = i - 1
# Run through the list of items (the left
# portion of the array) and find the correct position
# of the element referenced by `key_item`. Do this only
# if the `key_item` is smaller than its adjacent values.
while j >= left and array[j] > key_item:
# Shift the value one position to the left
# and reposition `j` to point to the next element
# (from right to left)
array[j + 1] = array[j]
j -= 1
# When you finish shifting the elements, position
# the `key_item` in its correct location
array[j + 1] = key_item
return array- O(n^2) : 버블 정렬같은 비효율적인 정렬 알고리즘이 이에 해당됩니다.
def bubble_sort(array):
n = len(array)
for i in range(n):
# Create a flag that will allow the function to
# terminate early if there's nothing left to sort
already_sorted = True
# Start looking at each item of the list one by one,
# comparing it with its adjacent value. With each
# iteration, the portion of the array that you look at
# shrinks because the remaining items have already been
# sorted.
for j in range(n - i - 1):
if array[j] > array[j + 1]:
# If the item you're looking at is greater than its
# adjacent value, then swap them
array[j], array[j + 1] = array[j + 1], array[j]
# Since you had to swap two elements,
# set the `already_sorted` flag to `False` so the
# algorithm doesn't finish prematurely
already_sorted = False
# If there were no swaps during the last iteration,
# the array is already sorted, and you can terminate
if already_sorted:
break
return array- O(2^n) : 피보나치 수를 재귀로 계산하는 알고리즘이 이에 해당되고, n^2과 혼돈할 수 있으며 처음에는 비슷해 보이지만 n이 5를 넘어가게 되면 2^n이 급격하게 커집니다.
# Function for nth Fibonacci number
def Fibonacci(n):
# Check if input is 0 then it will
# print incorrect input
if n < 0:
print("Incorrect input")
# Check if n is 0
# then it will return 0
elif n == 0:
return 0
# Check if n is 1,2
# it will return 1
elif 2 >= n:
return 1
else:
return Fibonacci(n-1) + Fibonacci(n-2)
# This code is contributed by Saket Modi
# then corrected and improved by Himanshu Kanojiya- O(n!) : 각 도시를 방문하고 돌아오는 가장 짧은 경로를 찾는 외판원 문제 "TSP(Traverling Salesman Problem)"를 브루트 포스(Brute Force) 로 풀이할 때가 이에 해당되며, 가장 느린 알고리즘으로 입력값이 조금만 커져도 웬만한 다항시간 내에는 계산이 어렵습니다.
[브루트 포스 검색(Brute Force Search)란? - 선형 구조를 전체적으로 탐색하는 순차 탐색, 비선형 구조를 전체적으로 탐색하는 깊이 우선 탐색(DFS, Depth First Search)과 너비 우선 탐색(BFS, breadth first search)이 가장 기본적인 도구이며, 알고리즘 설계의 가장 기본적인 접근 방법은 해가 존재할 것으로 예상되는 모든 영역을 전체 탐색하는 방법이다. // 출처 - https://hcr3066.tistory.com/26]
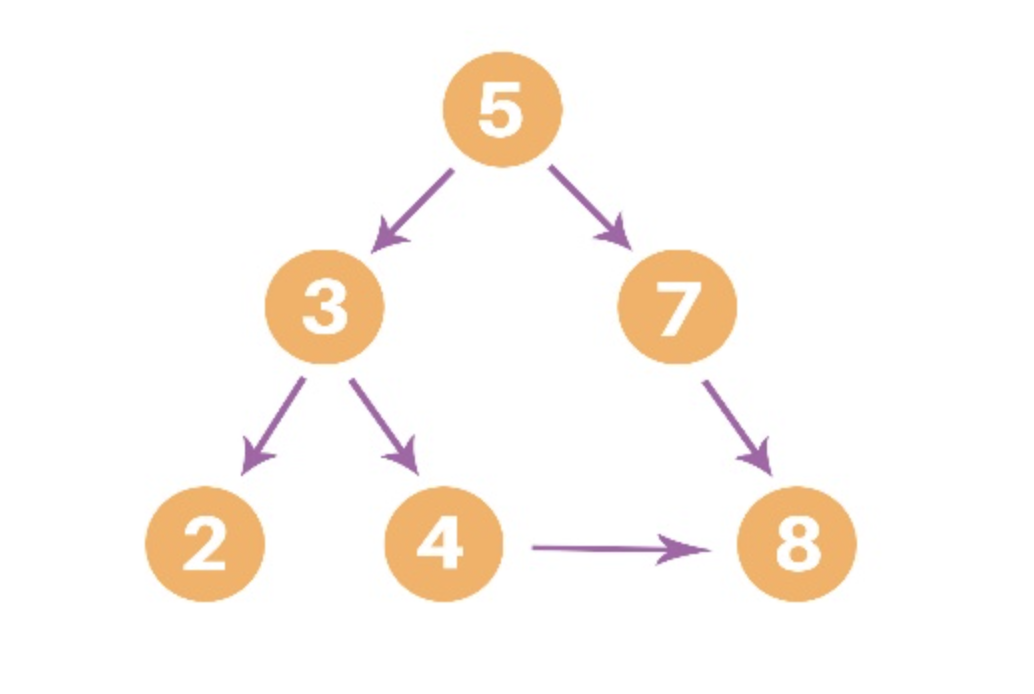
[출처 - https://favtutor.com/blogs/depth-first-search-python]
# Using a Python dictionary to act as an adjacency list
graph = {
'5' : ['3','7'],
'3' : ['2', '4'],
'7' : ['8'],
'2' : [],
'4' : ['8'],
'8' : []
}
visited = set() # Set to keep track of visited nodes of graph.
def dfs(visited, graph, node): #function for dfs
if node not in visited:
print (node)
visited.add(node)
for neighbour in graph[node]:
dfs(visited, graph, neighbour)
# Driver Code
print("Following is the Depth-First Search")
dfs(visited, graph, '5')빅오(O)는 시간 복잡도 외에도 공간 복잡도를 표현하는 데에도 널리 쓰입니다.
또한, 알고리즘은 흔히 실행 시간이 빠른 알고리즘은 공간을 많이 사용하고, 공간을 적게 차지하는 알고리즘은 실행 시간이 느린 "시간과 공간이 트레이드오프(Space-Time Tradeoff)" 관계입니다.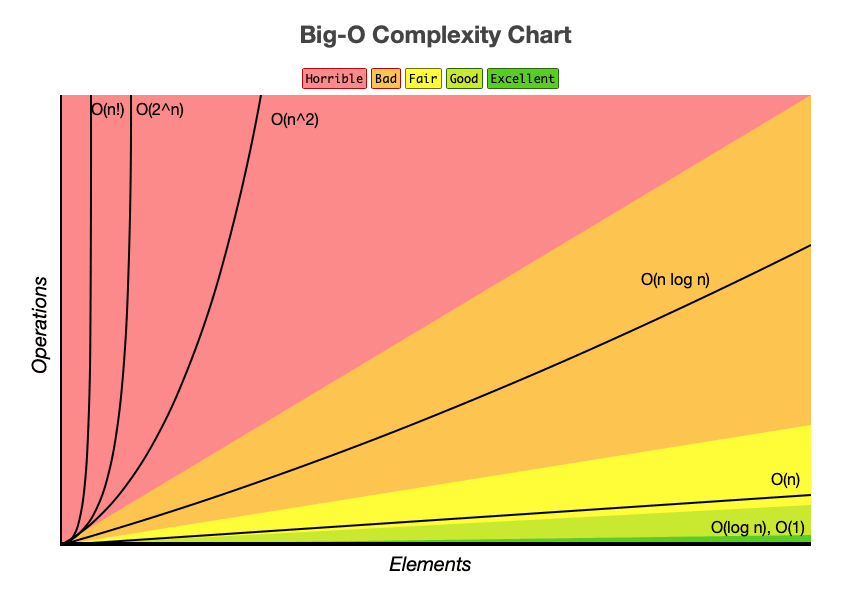
- 상한과 최악
빅오(O)는 상한(Upper Bound) 을 의미하고, 빅오메가(Ω)는 하한(Lower Bound) 을, 빅세타(θ)는 평균(Average) 을 나타냅니다
따라서, 빅오는(O)는 가장 늦게 실행될 때, 빅오메가(Ω)는 가장 빨리 실행될 때, 빅세타(θ)는 평균을 뜻 합니다.
여기서 주의할 점은 상한과 최악의 경우를 혼돈해서는 안됩니다.
빅오(O) 표기법은 주어진(최선/최악/평균) 경우의 수행 시간의 상한을 나타낸겁니다.
- 분할 상환 분석
시간 또는 메모리를 분석하는 알고리즘의 복잡도를 계산할 때, 알고리즘 전체를 보지 않고 최악의 경우만을 살펴보는 것은 지나치게 비관적이라는 이유로 분할 상환 분석 방법이 등장하는 계기가 됐습니다.
"분할 상환 분석(Amortized Analysis)"은 빅오(O) 와 함께 함수의 동작을 설명할 때 중요한 분석 방법 중 하나입니다.
최악의 경우를 여러 번에 걸쳐 골고루 나눠주는 형태로 알고리즘의 시간 복잡도를 계산할 수 있습니다.
예를 들어 커피머신을 충전하는데 10분, 총 10잔이 나오고 커피머신에 커피가 충전되어 있다면 10초면 커피를 마실 수 있겠지만, 운이 좋지 않아 다 떨어져 있다면 10분을 기다린 뒤에 마실 수 있습니다.
여기서 운이 좋다면 10초, 운이 좋지 않다면 10분이 걸립니다.
위를 예시로 100명의 사원이 커피를 가지러 갔다고 한다면 아무리 길어도 1,000분 정도의 시간이면 모든 사원이 커피를 마실 수 있다고 생각할 수 있습니다.
하지만 실제로 그 정도의 시간이 걸렸을까요? 아닙니다. 100명의 사원 중에서 커피를 만들어야 했던 사람은 10명뿐입니다. 따라서 이 사원들이 모두 커피를 마시는데 필요한 시간은 100분 정도를 넘지 않는다는 것을 알 수 있습니다. 다시 말하면, 각 사원이 커피를 마시기 위해서는 "평균적으로" 1분 정도의 시간이 필요하다고 결론을 내릴 수 있습니다.
[출처 - https://gazelle-and-cs.tistory.com/87]
- 병렬화
최근에는 딥러닝의 인기와 함께 병렬화가 큰 주목을 받고 있으며, GPU는 병렬 연산을 위한 대표적인 장치이기도 합니다.
GPU 각각의 코어는 CPU보다 훨씬 느리지만 GPU의 코어는 CPU의 코어보다 수백 배 더 많기 때문에 그만큼 연산을 동시에 수행 할 수 있습니다.
때문에 알고리즘 자체의 시간 복잡도 외에도 알고리즘이 병렬화가 가능한지는 근래에 알고리즘의 우수성을 평가하는 매우 중요한 척도 중 하나이기도 합니다.
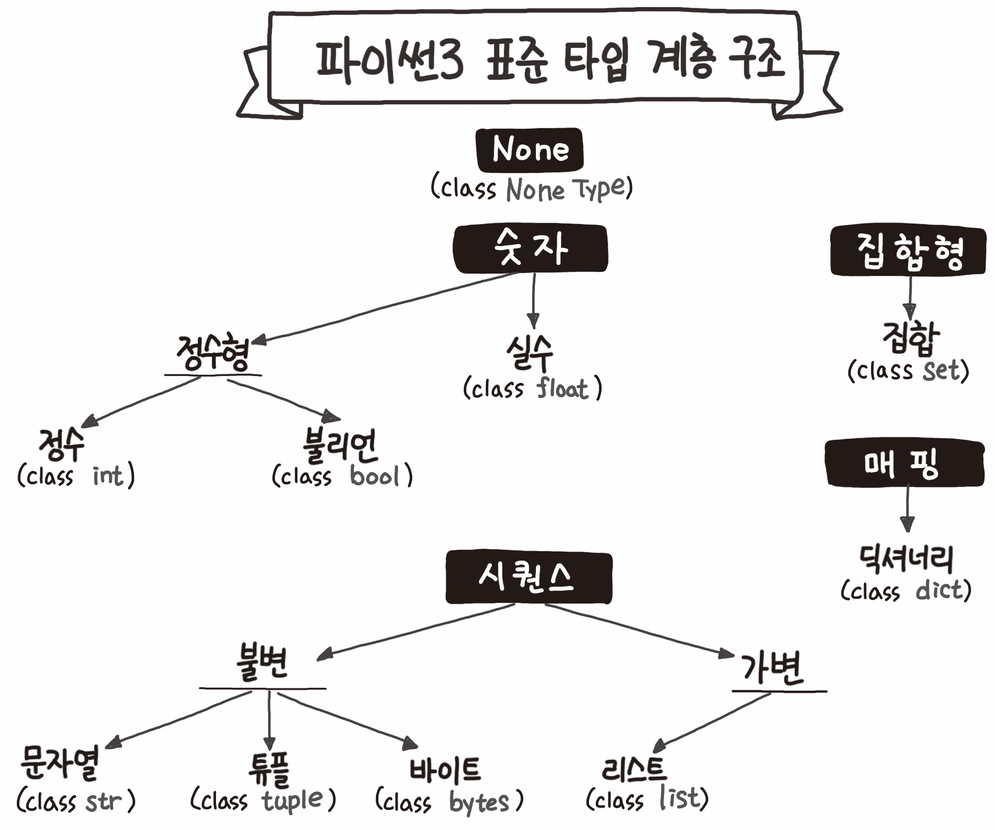
자료형
이 외에도 어떤 자료형을 요구하는지, 이들 자료형에는 어떠한 특징이 있는지 알아보겠습니다.
- 숫자
파이썬에서는 숫자 정수형으로 int만 제공합니다.
int는 C 스타일의 "고정 정밀도(Fixed-Precision)" 정수형이었고 long은 "임의 정밀도(Arbitrary-Precision)" 정수형이었습니다.
PEP 237을 통해 버전 2.4부터는 int가 충분하지 않으면 long타입으로 변경되는 구조가 됐으며, 덕분에 C와 달리 "오버플로(Overflow)"가 발생하는 일은 사라졌습니다.
또한, 3부터는 아예 int 단일형으로 통합되면서 int는 임의 정밀도를 지원하며, 더 이상 파이썬에서 고정 정밀도 정수형은 지원하지 않게 되었습니다.bool은 엄밀히 따지면 논리 자료형이지만, 파이썬 내부적으로 1(True)과 0(False) 으로 처리되는 int의 서브 클래스 입니다.
int는 object의 하위 클래스이기도 하기 때문에 다음과 같은 구조를 가졌습니다.
object > int > bool"임의 정밀도(Arbitrary-Precision)"란?
쉽게 말해 무제한 자릿수를 제공하는 정수형을 말합니다.
따라서 계산 속도는 저하되지만 숫자를 단일형으로 처리할 수 있으므로 언어를 매우 단순한 구조로 만들 수 있을 뿐만 아니라, 더 이상 오버플로를 고민할 필요가 없어 잘모된 계산 오류를 방지할 수 있게 되었습니다.
| 사이즈 | 1 | 1 | 1 | 3 |
|---|---|---|---|---|
| 갑 | 437976919 | 87719511 | 107 | 123456789101112131415 |
- 매핑(Mapping)
키(Key) 와 자료형(Value) 으로 구성된 복합 자료형이며, 파이썬에 내장된 유일한 매핑 자료형은딕셔너리(Dictionary)입니다.
딕셔너리는 키:밸류 로 값이 들어가 있으며, 키는 중복되지 않습니다.
- 집합(Set)
파이썬에서 집합 자료형인 set은 중복된 값을 갖지 않는 자료형입니다.
선언 해줄때는 딕셔너리(dictionary)와 동일하게 중괄호({}) 를 사용하여 선언해주기 때문에 혼란스러울 수 있으나, 차이점은 집합은 자료형으로만 값이 들어가고, 딕셔너리는 키와 밸류가 같이 들어가 있습니다.
my_set = {1, 2, 3}
my_dictionary = {1:'a', 2:'b', 3:'c'}- 시퀀스(Sequence)
-
우리말로 하면
'수열'같은 의미로, 어떤 특정 대상의 순서있는 나열을 뜻합니다.
예를 들어 str은 문자의 순서 있는 나열로 문자열을 이루는 자료형이며, list는 다양한 값들을 배열 형태의 순서 있는 나열로 구성하는 자료형입니다.
때문에 파이썬은 list라는 시퀸스 타입이 사실상 배열의 역할을 수행합니다. -
시퀸스는 값을 변경할 수 없는
불변(Immutable)[str, tuple, bytes] 과 변경이 가능한가변(Mutable)[list, dict] 으로 구분합니다.a = 'abc' id('abc') -> 4336057456 id(a) -> 4336057456 a = 'def' id('def') -> 4336933872 id(a) -> 4336933872변수 'a'의 값은 변경이 가능하지만, 불변이라 한 이유는 위에 코드 결과값에서 알 수 있듯이 str('abc', 'def')이 저장된 주소를 참조한 것을 변경한것 뿐이지 실제로 값을 변경한 것은 아닙니다.
a[1] = 'd' -> TypeError: 'str' object does not support item assigment때문에 위와같은 코드를 작성하면 타입에러가 나옵니다.
정적배열인 str과 달리 가변인 list는 자유롭게 값을 추가, 삭제할 수 있는 동적 배열입니다.
-
-
원시 타입
C 나 Java 같은 대표적인 프로그래밍 언어들은 기본적으로 "원시 타입(Primitive Type)"을 제공합니다.
특히 C 언어는 동일한 정수형이라도 크기나 부호에 따라 매우 다양한 원시 타입을 제공합니다.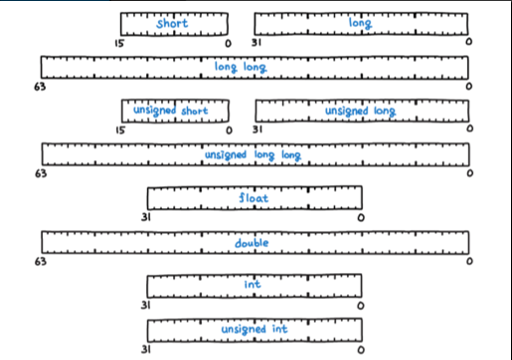
원시 타입은 정확하게 메모리를 타입 크기만큼의 공간을 할당하고 그 공간을 오로지 값으로 채워 넣습니다.
만약 배열이라면 "물리 메모리(Physical Memory)"에 자료형의 크기만큼 공간을 갖는 요소가 연속된 순서로 배치되는 아래의 그림과 같은 형태가 됩니다.
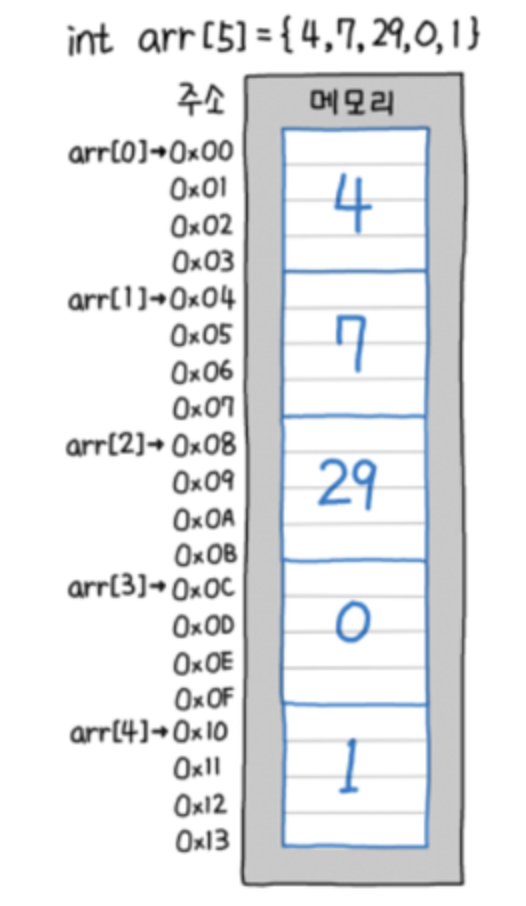
원시 타입은 매우 빠른 연산이 가능합니다.
아울러 Java는 원시 타입에 대응되는 클래스 "객체(Object)"를 지원하며, 단순히 메모리에 숫자만 보관하고 있을 때는 하지 못했던 문자로 변환하거나, 진법 변환, 시프팅(Shifting)"[컴퓨터가 읽는 비트(bit)를 이동시켜 빠르게 연산하는 방법] 같은 비트 조작을 할 수 있습니다.
다만 이를 위한 여러 가지 부가 정보가 추가되므로, 메모리 점유율이 늘어다고 당연히 계산 속도 또한 감소 됩니다. -
파이썬은 애초에 편리한 기능 제공에 우선순위를 둔 언어인 만큼 원시 타입을 제공하지 않으며, 느린 속도와 더 많은 메모리를 차지하더라도 훨씬 더 다양한 기능을 제공할 수 있는 객체만 지원합니다.
| 언어 | 지원 타입 형태 |
|---|---|
| C | 원시 타입 |
| Java | 원시 타입, 객체 |
| Python | 객체 |
- 객체(Object)
파이썬은 모든 것이 객체입니다.
이 중에서 크게 "불변 객체(Immutable Object)" 와 "가변 객체(Mutable Object)"로 구분할 수 있는데, 이전에 "시퀸스(Sequence)"의 경우에도 불변과 가변을 구분해 정리했으나, 이 외에도 정리해보려고 합니다.
| 클래스 | 설명 | 불변 객체 |
|---|---|---|
| bool | 부울 | O |
| int | 정수 | O |
| float | 실수 | O |
| list | 리스트 | X |
| tuple | 리스트와 튜플의 차이는 불변 여부이며, 이외에는 거의 동일합니다.(튜플은 불변이므로 생성할 때 설정한 값은 변경할 수 없습니다.) | O |
| str | 문자 | O |
| set | 중복된 값을 갖지 않는 집합 자료형 | X |
| dict | 딕셔너리 | X |
- 반복 가능한 객체와 시퀸스의 차이
요소의 순서가 정해져 있고 연속적으로 이어져 있으면 시퀀스 객체, 요소의 순서와는 상관없이 요소를 한 번에 하나씩 꺼낼 수 있으면 반복 가능한 객체입니다.
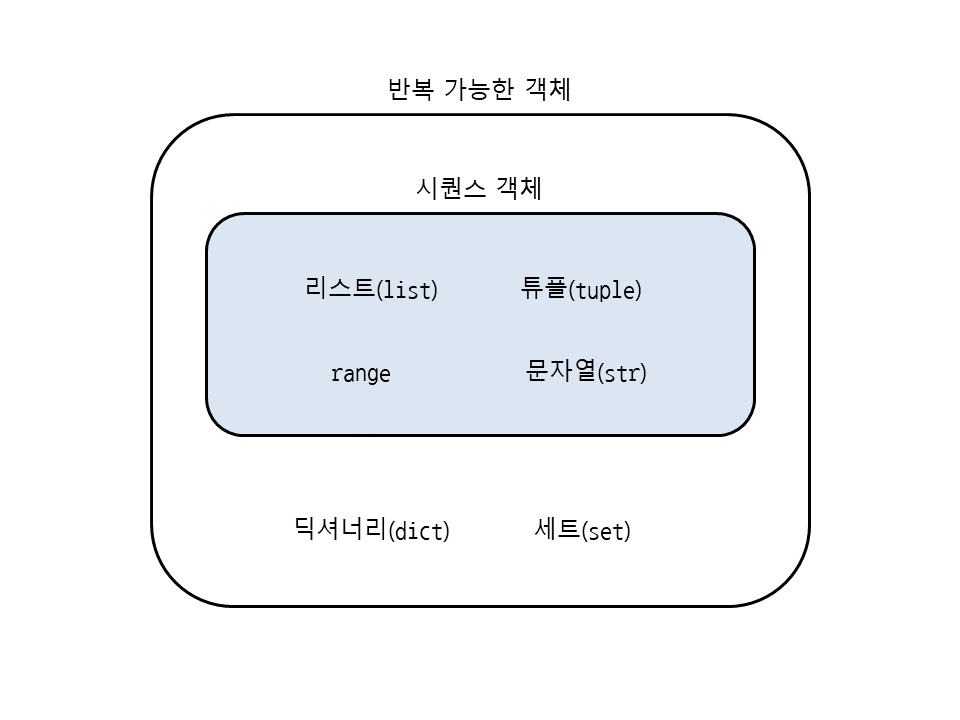
[출처 - https://dojang.io/mod/page/view.php?id=2405#:~:text=%EB%94%B0%EB%9D%BC%EC%84%9C%20%EC%8B%9C%ED%80%80%EC%8A%A4%20%EA%B0%9D%EC%B2%B4%EA%B0%80%20%EB%B0%98%EB%B3%B5,%EC%9E%88%EC%9C%BC%EB%A9%B4%20%EB%B0%98%EB%B3%B5%20%EA%B0%80%EB%8A%A5%ED%95%9C%20%EA%B0%9D%EC%B2%B4%EC%9E%85%EB%8B%88%EB%8B%A4.]
- 참조(Reference)와 파이썬의 참조 할당 방식의 차이점
c++에서 참조 변수는 변수의 값을 할당하면 참조의 대상 또한 할당된 값으로 변경됩니다.
다만, 파이썬은 동일한 메모리 주소를 가리키지만, 새로운 값을 할당하게 되면 기존 메모리 주소값을 참조하지 않고 새로운 객체를 참조하게 됩니다.
- c++
int a = 10;
int &b = a;
b = 7
std::cout << a << std::endl;
-> 7- python
a = 10
b = a
id(a), id(b)
-> 4370999104 4370999104
b = 7
id(a), id(b)
-> 4370999104 4370999008문자나 숫자 같은 불변 객체는 값의 변경이 불가능하기 때문에 이처럼 참조 변수에서 값을 바꿀수 없지만, list와 같은 가변 객체를 참조하고 있다면 참조 변수에서 값을 변경할 수 있다.
a = [1, 2, 3]
b = a
id(a), id(b)
-> 4337584832 4337584832
b[1] = 5
a
-> [1, 5, 3]
id(a), id(b)
-> 4337584832 4337584832- is와 ==
파이썬의 비교 연산자 중 is와 ==가 있으며, 이둘의 관계는 파이썬의 객체 구조와 관련이 깊습니다.
is는 id() 값(객체 메모리) 을 비교하는 함수이며, None은 널(null)로서 값 자체가 정의되어 있지 않아 ==로 비교가 불가능합니다.
반대로 ==은 변수가 참조하는 값(객체) 을 비교합니다.
a = [1, 2, 3]
a == a
-> True
a == list(a)
-> True
a is a
-> True
a is list(a)
-> False
# 값은 동일하지만 list()로 한 번 더 묶어주면, 별도의 객체로 복사가 되고 다른 ID값을 가지게 됩니다.
a == copy.deepcopy(a)
-> True
a is copy.deepcopy(a)
-> False
# copy.deepcopy()로 복사한 결과 값은 같지만 ID값은 다릅니다.- 속도
파이썬의 객체 구조는 잘 설계되어 있고 매우 편리하면서 강력하지만 문제는 속도입니다.
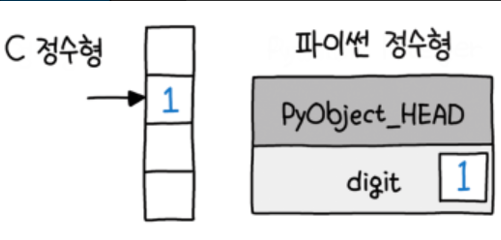
단순한 정수형의 덧셈 연산을 하는 경우엔 메모리에서 값을 꺼내 한번 연산하는 원시 타입에 비해, 파이썬의 객체는 값을 꺼내는 데만 해도 val->PyObject_HEAD에서 타입코드를 찾는 등 여러 단계의 부가 작업이 필요합니다.
파이썬도 C 와 Java처럼 빠른 속도를 내려면 C 로 만든 과학 계산 모듈인 넘파이(Numpy)를 사용해야 합니다.
%timeit -n 100 np.std(numpy_rands)
-> 3.28 ms
%timeit -n 100 standard_deviation(rands)
-> 131 ms
- 넘파이(numpy) 배열을 이용한 표준편차 계산 시간 : 3.28밀리초
- 파이썬 리스트를 이용한 표준편차 계산 시간 : 131밀리초 // 약 40배 이상 차이- 자료구조, 자료형, 추상 자료형의 차이점
- 자료형은 컴파일러 또는 인터프린터에게 프로그래머가 데이터를 어떻게 사용하는지를 알려주는 일종의 데이터 속성(Artribute)입니다.
- 자료구조는 일반적으로 원시 자료형을 기반으로 하는 배열, 연결 리스트, 객체(Object) 등을 말하고, 데이터에 효율적으로 접근하고 조작하기 위한 데이터의 조직, 관리, 저장 구조 입니다.
- 추상 자료형은 일반적으로 줄여서 ADT라 부르며 자료형에 대한 수학적 모델을 지칭합니다.
정리하자면 ADT란 해당 유형의 자료에 대한 연산들을 명기한 것으로, 행동만을 정의할 뿐 실제 구현방법은 명시하지 않아 "객체 지향 프로그래밍(Object-Oriented Programming)"의 "추상화(Abstraction)"와 비슷한 개념이라 할 수 있습니다.