Dynamic Programming

DP(Dynamic Programming)을 위한 3가지 조건

1. problem이 더 작은 sub problem으로 쪼개질 수 있을 때
2. sub problem의 sollution으로 더 큰 규모(problem) 의 sollution을 구할 수 있을 때
3. sub problem들이 겹칠 때

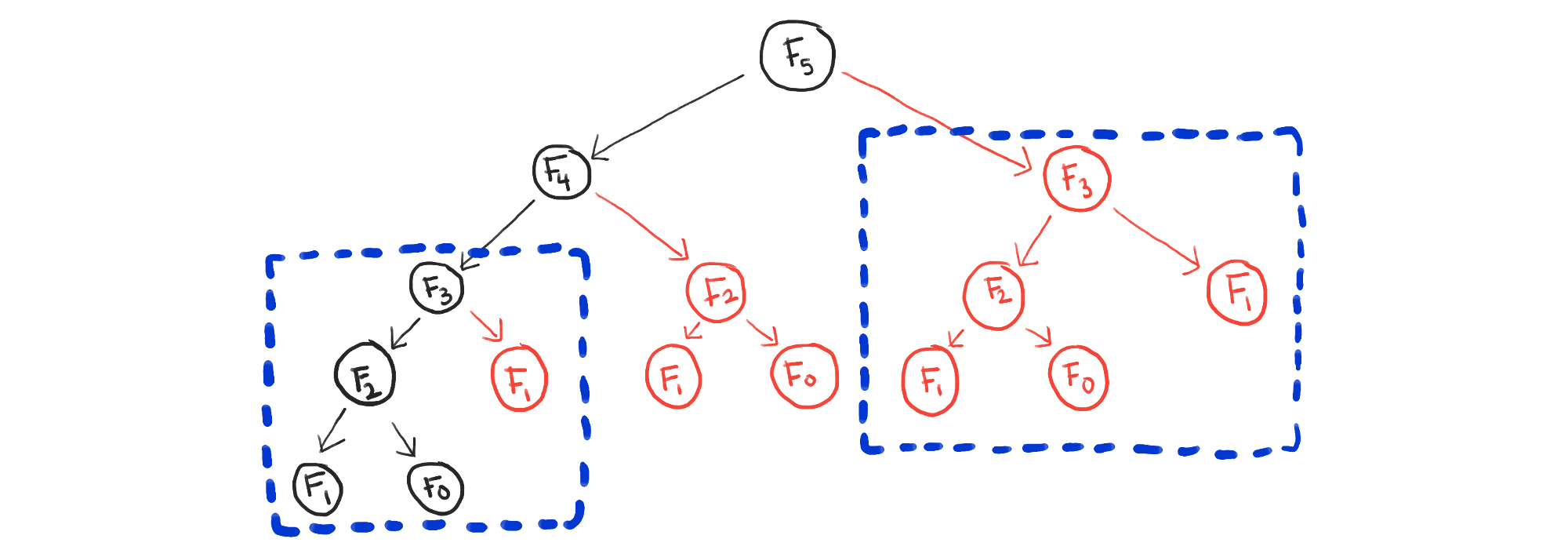
• Fibonazzi는 첫 번째 항과 두 번째 항이 1이며, 그 뒤의 모든 항은 구하고자 하는 항의 이전과 이전전을 합한 수열입니다.
  이를 재귀(Recursion)을 통해서 아래와 같이 코드를 작성하였고, 시간 복잡도는 O(2^n)입니다.

  def fib_naive(n):
      if 0 == n:
          return 0
      elif 1 == n:
          return 1
      else:
          fib = fib_naive(n-1) + fib_naive(n-2)
          return fib

  %timeit fib_naive(35)
  -> 16.3 s ± 1.76 s per loop

---

• Top-Down 방식[recursive DP - arr를 활용]
  arr 에 계산된 값을 저장하는, 메모이제이션(memoization) 을 통해서 단순한 재귀 함수보다 계산 수를 많이 줄일 수 있고, 시간이 많이 단축 되지만
  특정 이상의 큰 수를 인자값으로 넣을 경우, Problem(Top)을 위한 sub probelm(Down)을 계산하기 때문에 함수를 호출할 때마다 stack에 메모리가 쌓이게 되어, StackOverflow가 발생 됨.
  • 메모이제이션(memoization)은 컴퓨터 프로그램이 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술이다. 동적 계획법의 핵심이 되는 기술이다.

  fib_arr = [0, 1]
  
  
  def fib_recur_dp(n):
  	if n < len(fib_arr):
    	return fib_arr[n]
    else:
    	fib = fib_recur_dp(n-1) + fib_recur_dp(n-2)
        fib_arr.append(fib)
        return fib

    %timeit fib_recur_dp(35)
    -> 860 ns ± 514 ns per loop

O(n)의 시간 복잡도를 가지고 있으며, 10만의 수를 인자값으로 넣을 경우 call stack이 한계(Limited)를 넘어서 overflow로 인한, RecursionError를 일으킵니다.

fib_recur_dp(100000)
-> RecursionError: maximum recursion depth exceeded while calling a Python object

---

• Bottom-Up 방식
  Top-Down과 동일하게 arr에 계산된 값을 저장하는 memoization 방식이지만, 차이점은 sub problem(Bottom)부터 problem(Up)으로
  계산하는 방식의 차이가 있으며, 가장 최근(problem)의 계산된 값을 제외한 값(Sollution) 은 삭제할 수 있기 때문에
  메모리를 절약할 수 있고, 함수를 재귀적으로 호출하지 않아 호출할 때 발생되는 CallStack이 메모리에 올라가는 것도 방지가 되어
  Overflow를 예방합니다.
  • 시간 복잡도도 O(n)이지만, 최선으로 O(1) 까지도 줄일 수 있습니다.

def fib_dp(n):
	if 0 == n:
    	return 0
    elif 1 == n:
    	return 1
    fib_arr = [0, 1]
    
    for i in range(2, n+1):
    	num = fib_arr[i-1] + fib_arr[i-2]
        fib_arr.append(num
    return fib_arr[n]
    
%timeit fib_dp(35)
-> 12.8 µs ± 4.83 µs per loop

때문에 이전에 Overflow가 발생된 Top-Down방식과 다르게 동일한 10만을 Bottom-Up방식으로는 빠르게 계산이 가능합니다.

%timeit fib_dp(100000)
-> 265 ms ± 132 ms per loop

이렇게 유용한 DP(Dynamic Programming) 이지만, DP를 하기 위해선 위에서 봤던 3가지 조건이 있으며, 이에 해당되는 조건 중 problem과
sub problem을 정의하는 것이 초보자에게 어려우며, 이를 극복하기 위해서는 알고리즘 문제들을 풀어가며 익숙해져야 합니다.

모든 코드는 google colab으로 진행했으며, 유튜버 "코드없는 프로그래밍"님의 영상으로 학습하였습니다.
이미지 출처 - https://hiringfor.tech/2020/10/26/my-resources-for-dynamic-programming.html