1. 단순회귀모형, 회귀계수

단순회귀 모형 정의

단순회귀 모형의 기본적인 가정

회귀계수 추정량

---

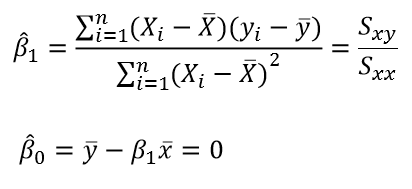
2. 최소제곱추정량의 표본분포

회귀모형의 mean-corrected 형태

앞에서 정의한 회귀모형이 단순회귀 모형의 기본적인 가정을 만족한다고 하자.
회귀모형을 mean-corrected 형태로 표현하면 다음과 같다.

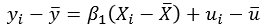
📌 회귀모형의 mean-corrected 형태 유도(증명)

---

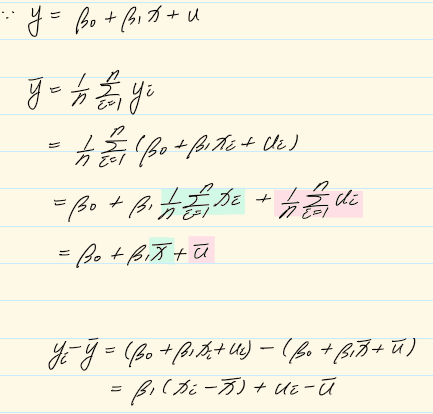
회귀계수 추정량의 재표현

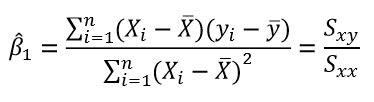
위의 추정량에서 분자를 아래와 같이 변환할 수 있다.
분자의 변환값을 이용해 $\beta_1$hat(추정량)을 재표현할 수 있다.

---

중심극한정리에 의한 성질

1. 재표현한 식의 2번째 항 분자를 다시 살펴본다.
   

2. 다음이 성립함을 확인한다.
   

3. $\beta_1$hat 의 분모는 $n$이 충분히 크면 다음과 같이 주어진다.

---

Slustky Theorem

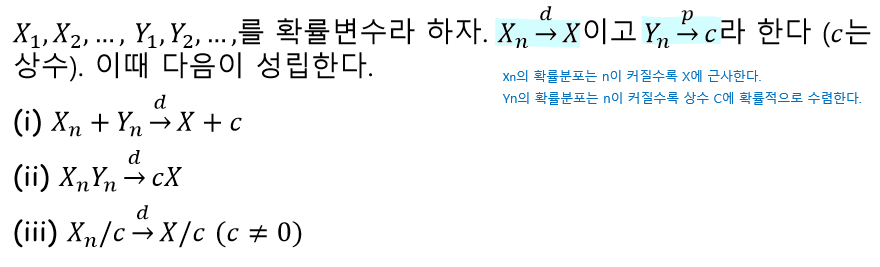
Slustky 정리에 의해 $\beta_1 hat - \beta_1$ 의 분포를 유도한다. 먼저 아래의 참고사항을 복기해보자.

📌 Slustky 정리에 의한 $\beta_1 hat - \beta_1$ 의 분포
유사하게 다음이 성립한다.

---

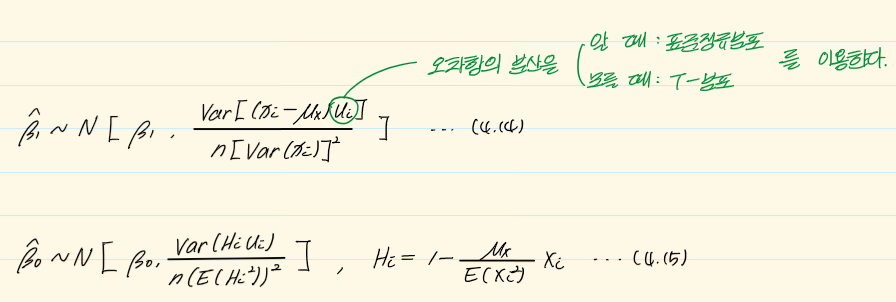
💡 질문과 피드백 사항은 댓글에 편하게 남겨주시기 바랍니다.
❤️ 도움이 되셨다면 공감 부탁드립니다.