1. $\hat\beta_1$ 가설검정

다음의 가설검정을 생각해보자.

표준오차 $S.E(\hat\beta_1)$

: 표본 통계량의 표준 편차

$T$-통계량

: 모집단의 분산이나 표준편차를 알지 못할 때, 모집단을 대표하는 표본으로부터 추정된 분산이나 표준편차를 가지고 검정하는 방법으로 “두 모집단의 평균간의 차이는 없다”라는 귀무가설과 “두 모집단의 평균 간에 차이가 있다”라는 대립가설 중에 하나를 선택할 수 있도록 하는 통계적 검정방법

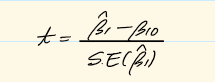
유의확률 $p-value$

: 우리가 뽑은 데이터로부터 구한 값인 표본평균($\hat X$)보다 더 극단적인 값이 뽑힐 확률
$cf$) 유의수준 : 더 극단적으로 나올 확률이 어느 정도 되어야 귀무가설을 기각할 것인가? 에 대한 기준. 귀무가설을 기각시킬 기준이 되는 확률. 즉, 커트라인

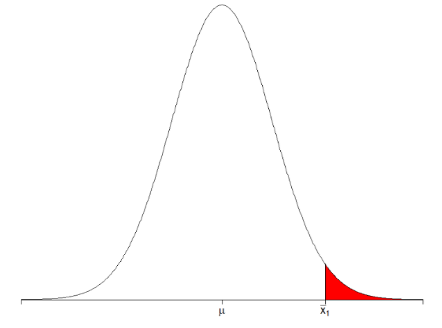
cf) 유의수준$\alpha$ & $p-value$ 에 대해 가장 간단하고 명료하게 설명한 글입니다.
http://hsm-edu.tistory.com/135

---

2. $\hat\beta_1$ 신뢰구간

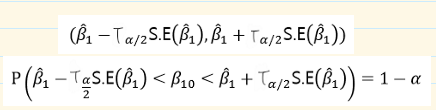
$cf)$ T검정과 Z검정의 차이

신뢰구간의 의미

95% 신뢰구간이란 예를 들어, 100개의 신뢰구간 중 모수값 $\beta_1$을 포함하는 신뢰구간의 개수가 95개라는 의미이다.

※ 우리 식에서 변하는 값은 모수가 아닌 신뢰구간이다.

• "모수"가 신뢰구간에 포함될 확률이 95%이다. (X)
• "신뢰구간"이 모수를 포함할 확률이 95%이다. (O)
  

---

💡 질문과 피드백 사항은 댓글에 편하게 남겨주시기 바랍니다.
❤️ 도움이 되셨다면 공감 부탁드립니다.